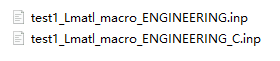RVE多尺度模拟方法-理论与案例
本文摘要(由AI生成):
本文介绍了使用S的Material Designer进行单胞模型分析的过程。文章指出,不同软件在单胞模型支持方面略有差异,但主要目标都是比较谁家支持的单胞模型更丰富。文中详细描述了如何在Material Designer中设置纤维增强材料的参数,包括纤维体积占比、单元类型和网格尺寸等,并通过运行程序得到相关统计数据和网格模型。此外,文章还探讨了纤维和基体材料参数的输入,以及等效宏观材料参数的计算方法。虽然文章提及了一些技术细节和疑问,但总体上,单胞模型分析的过程相对简单,主要涉及建立单胞、加载和测量等效材料参数,然后应用于宏观模型分析。
“ 使用代表体积元方法描述材料本构”
这依然是一篇学习笔记。
书接上回
经典的弹性、弹塑性力学理论能够描述许多材料的行为。但对于一些特殊的材料,其微尺度下的结构特征对宏观响应有很大的影响。但你要是把所有微尺度特征都用有限元建模画出来,那它的单元数就不知道要多到哪里去了。这种情况下,就需要“均匀化方法”闪亮登场,来解决这种跨尺度的问题。对于更复杂一点的情况,还可以对宏观、细观两个尺度的连续介质(注意即使是细观也得是连续介质哦)分别做有限元分析,使用细观尺度的分析结果来预测微结构中的状态,并获得宏观的材料参数。这种首先模拟微尺度结构特征的做法,被模拟的微尺度单胞就被称为代表体积元(representative volume element RVE)。微尺度分析得到的等效材料参数被用于宏观分析中,宏观分析得到的位移结果又被作为微尺度的边界条件,进一步分析微观结构的细节应力和应变。这两种尺度的分析加在一起,在一些文献中也被叫做 FE^2 方法。
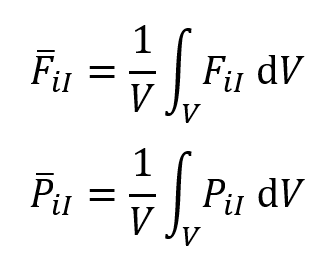
F和P分别是变形梯度张量,和第一 P-K应力。等式左侧是宏观均匀化的量,右侧是微观量。意思就是说微观尺度的应变和应力,在体积平均积分后要与宏观值相等。
简单调研了一圈各家大厂提供的多尺度模拟工具以后,笔者决定先来了解一下Altair家的这款Multiscale Designer。毕竟据Altair官方在文档中的说法,这款工具提供了无与伦比的 易用性、计算效率、仿真准确性 和 功能丰富性嘛。


对于Multiscale Designer来说,主要有两大类工作流。分别是确定性分析 和 随机性分析。Deterministic and Stochastic。确定性分析,指的是微尺度的结构几何特征都是完全确定的。无论是已知微尺度所有信息,正向获得宏观均匀化材料参数,还是已知宏观参数和微观结构特征反推微观的尺寸参数,都有成熟的工具可用。
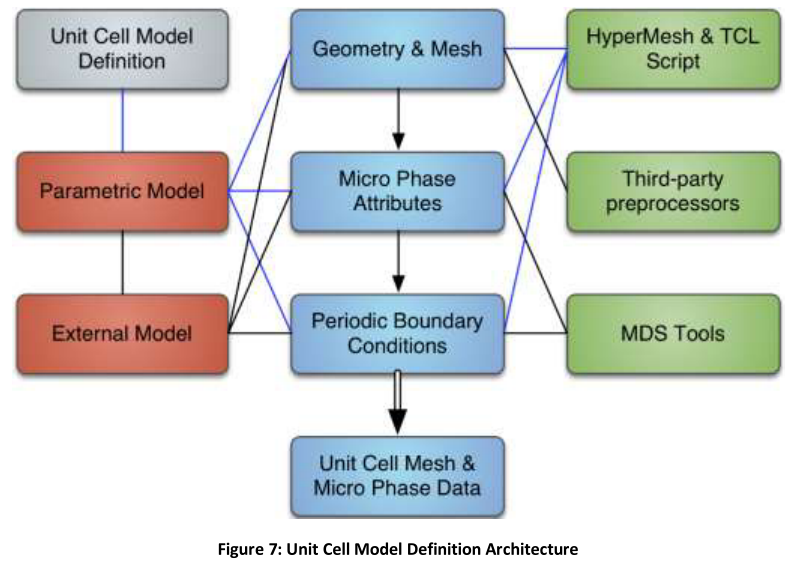
随机性分析,用于考虑微观尺度中的几何形状和本构特征可变且随机分布的一类材料。例如常见的各种短纤维增强材料、夹杂材料等等。软件可以计算一个概率分布函数(Probability Distribution Function,后面会简写为PDF。也不知道这个缩写是咋想的要跟文档格式撞车),来描述这种微观几何与本构可变材料对应的宏观尺度特性。流程图大概就像下面这样。MDS大概是Multiscale DeSigner的缩写。
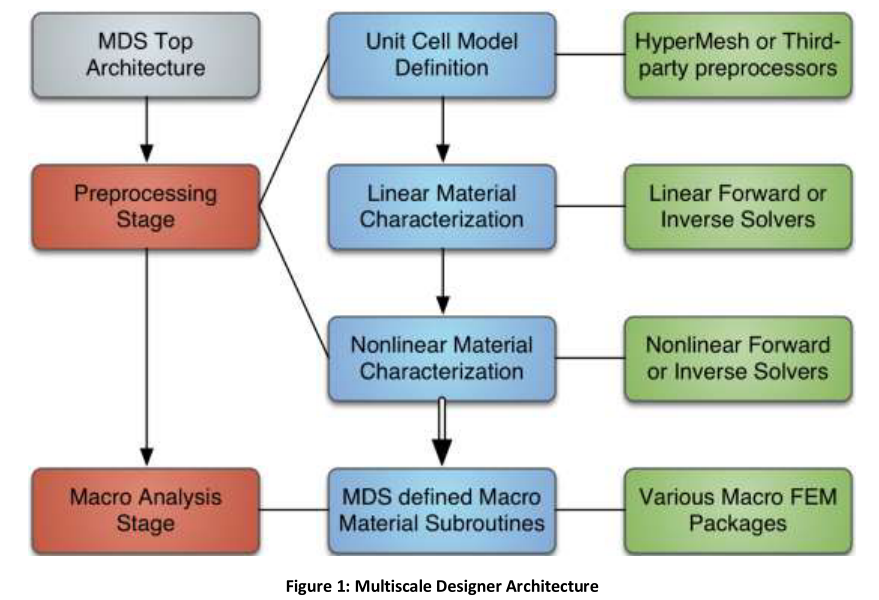
流程图中可见,主要分析过程就分为前处理(细观)和宏观分析两个阶段。在前处理阶段,根据单胞特征得到均匀化材料属性;宏观分析阶段,使用得到的材料参数或相应的用户自定义材料宏,调用各种宏观有限元分析软件完成求解。对于单胞定义流程,Multiscale Designer充分发挥了Altair家软件心胸开放的优良传统。不仅支持自己创建单胞参数化模型,也支持导入HyperMesh甚至第三方前处理软件建立好的单胞模型。
说了这么多,没有案例操作总觉得是在纸上谈兵,不落地。那么就来简单做一个Tutorial案例玩玩。
这软件的全名写着太麻烦。但Multiscale Designer如果简称MD的话,不仅和ANSYS家的Material Designer傻傻分不清,而且就在仿真相关领域,分子动力学(Molecule Dynamics 简称MD)这个名字也更为响亮。后文我们就遵循Altair文档中的写法,将它简称为MDS吧。
安装HyperWorks后可以在开始菜单找到MDS,打开发现它的主界面简洁的有些过分。对,就这么小,这么几个按钮,还都是灰色的。
那,我们点一点左上角那个新建按钮,新建一个项目来玩玩看。
好的,现在这些按钮亮起来了。可以看到MDS软件分为确定性分析和随机分析两大类功能。那我们点一下Unit Cell Model Definition,单胞模型定义。
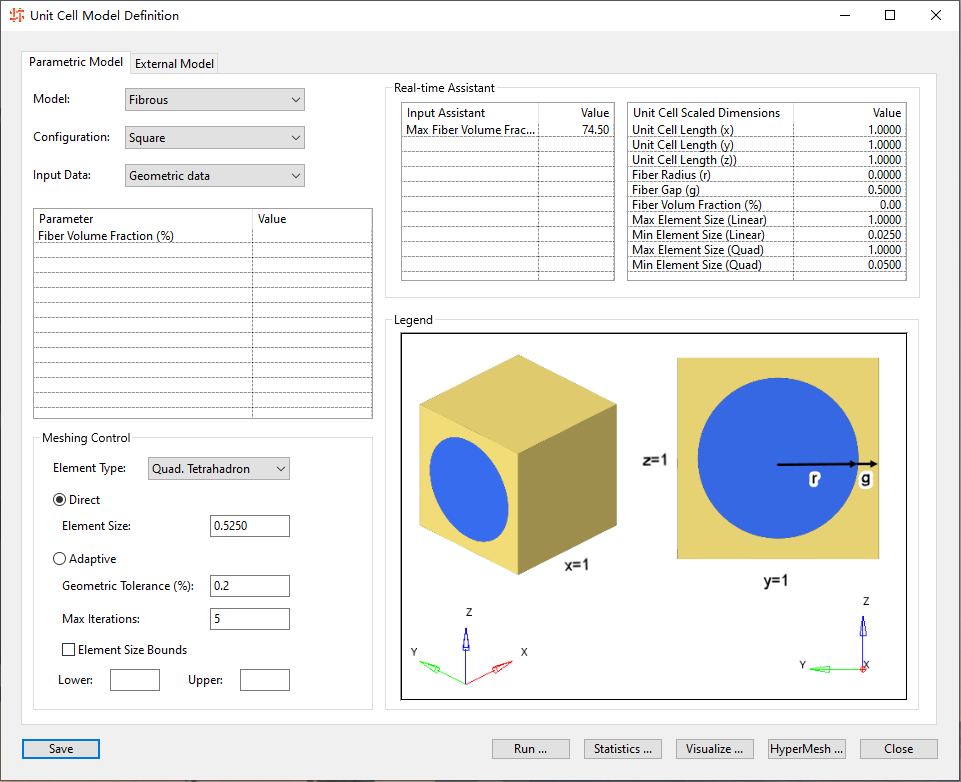
整体界面长下面这样。其实很好理解,就是有一些预设的单胞模板,其中某些尺寸被参数化了,在右侧填数就行。这东西和ANSYS的Material Designer其实差不多(换句话说基本上不管谁来做差不多都会做成这种附图填空写参数的样子)。更多的就是比比看谁家支持的单胞模型更丰富了。
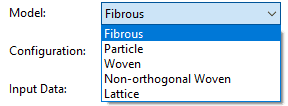
Model里面,2022版本支持纤维、粒子、织物、非正交织物、晶格等结构。
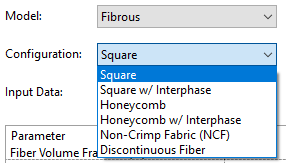
例如这个Honeycomb蜂巢构型。以及后面跟着的 w/ Interphase,指的是纤维和基体之间还包含一层界面。

那我们先用最简单的纤维增强材料,Square构型,填一个纤维体积占比,就30%吧。单元类型选二阶,自适应网格尺寸。
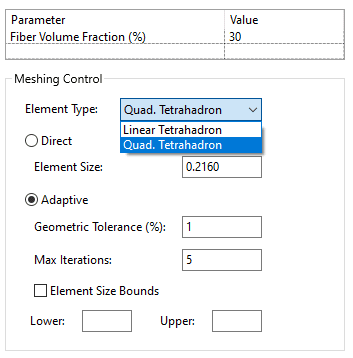
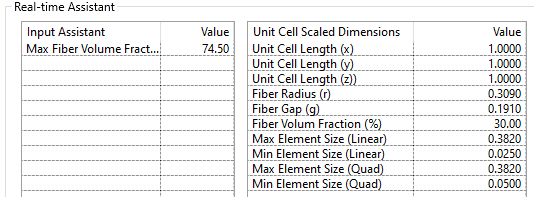
界面右侧,我输入体积占比30%,其他相关特征参数就都帮我算好了。比如在单位立方体中,纤维的半径啊、缝隙尺寸啊等等。

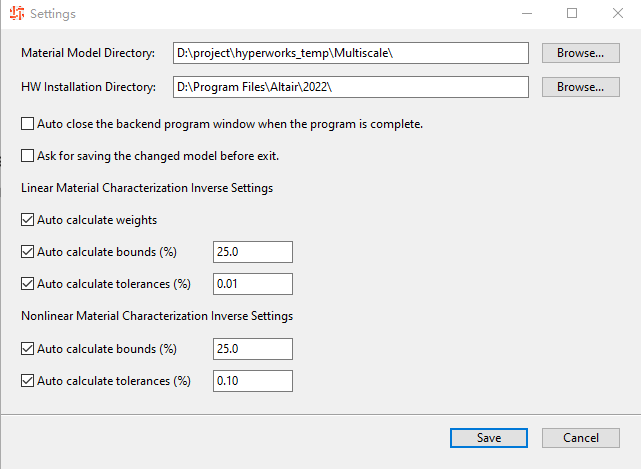
需要在设置里正确定义HyperWorks的安装目录。
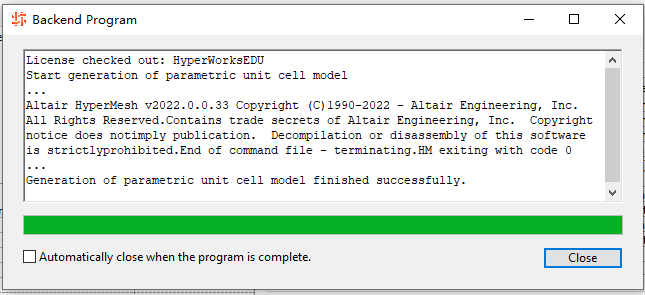
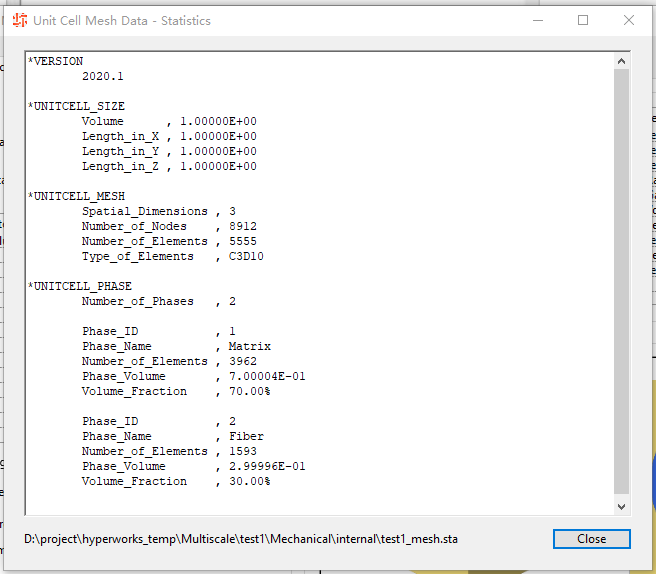
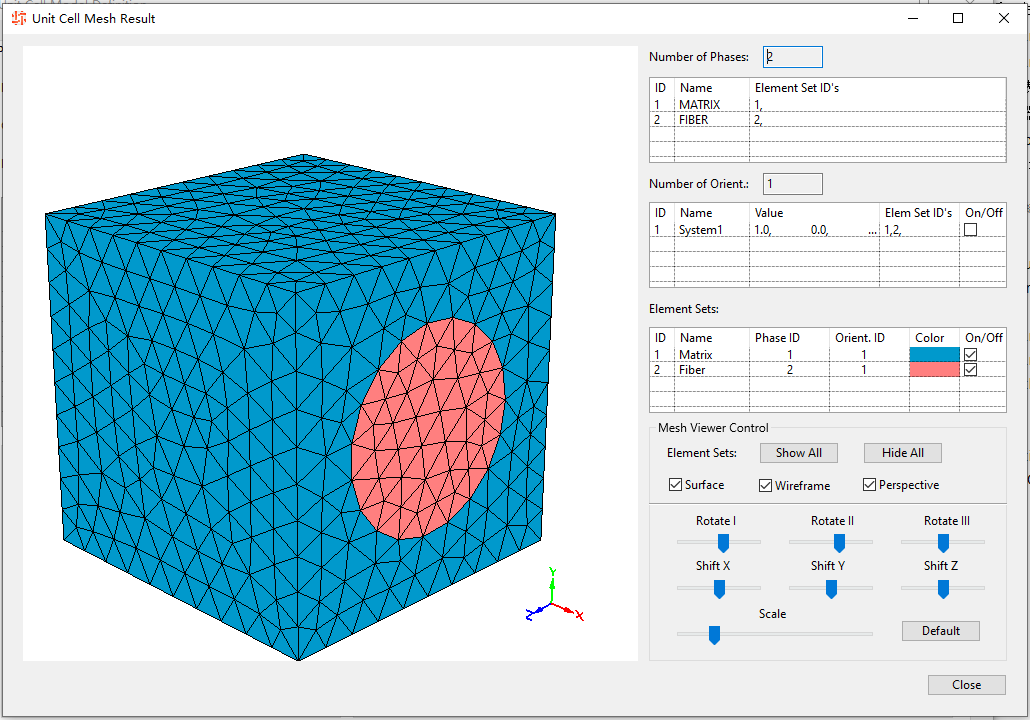
还可以点击HyperMesh,直接唤起HM查看网格模型……从刚才我就想吐槽,这东西其实就是Altair官方基于HyperMesh二次开发的一个小插件而已吧。功能全面一点,给它起了个名字就变成一个独立的软件产品了。把刚才的窗口关掉,可以看到第二项 Linear Material Characterization已经可用。
我们来给它提供一套纤维和基体的材料参数。这里就假设纤维的弹性模量是基体的10倍吧。

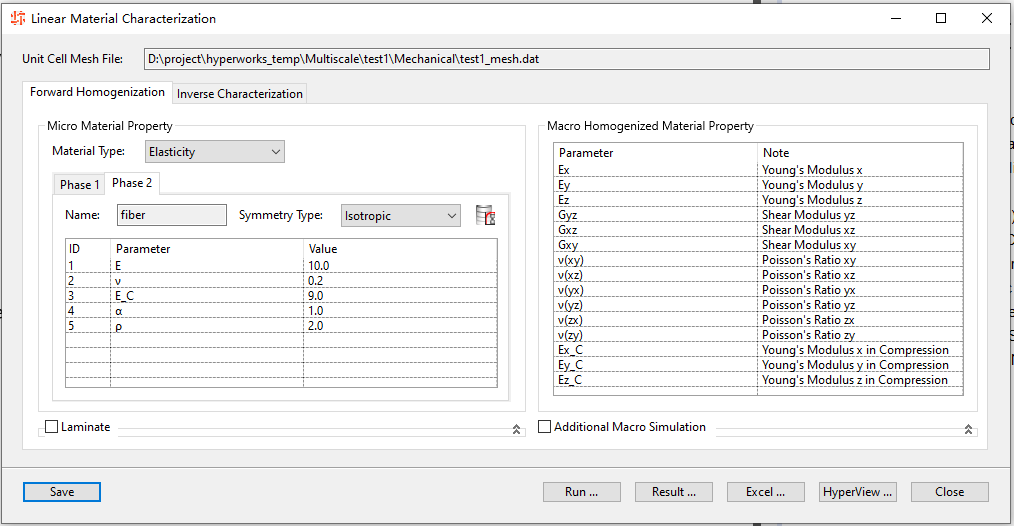
说实在的,这里的E_C指的是压缩模量。这里默认支持纤维和基体拉-压弹性模量不同还是挺让人惊讶的。就是这个参数之间的关系……非常的让人无法理解。根据MDS的帮助文档介绍,泊松比 v (其实应该是希腊字母\nu,这里暂且用v代替)的取值范围在 -1 < v < 0.5。允许负泊松比存在。而拉伸和压缩弹性模量确定以后,压缩泊松比则根据其余三个数值计算得出:

但这儿这个公式,我就不是十分理解。这是为了保证剪切模量 μ 在拉伸和压缩时的一致吗?可是其他地方的拉压不同材料,都是优先确保刚度矩阵的对称性啊。(往后看,后附解答)

忽略这些疑问,填了两相材料参数后,点击Run,即算出相应的宏观均匀化材料参数。
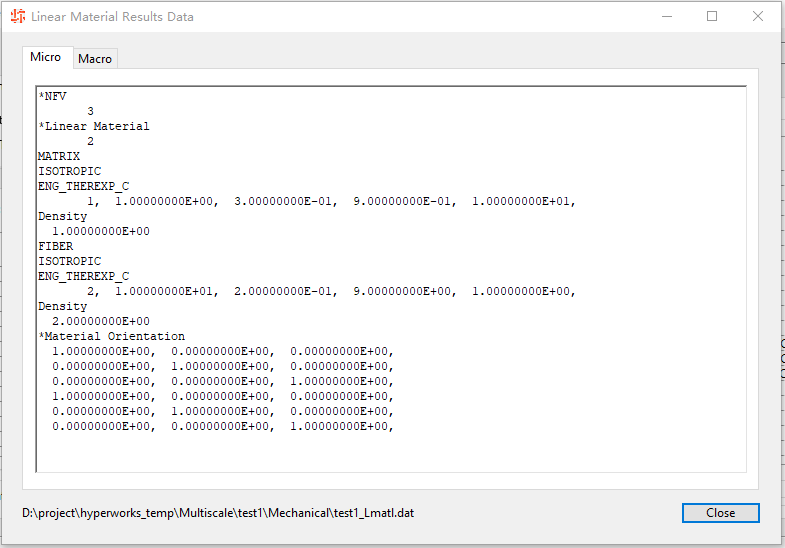
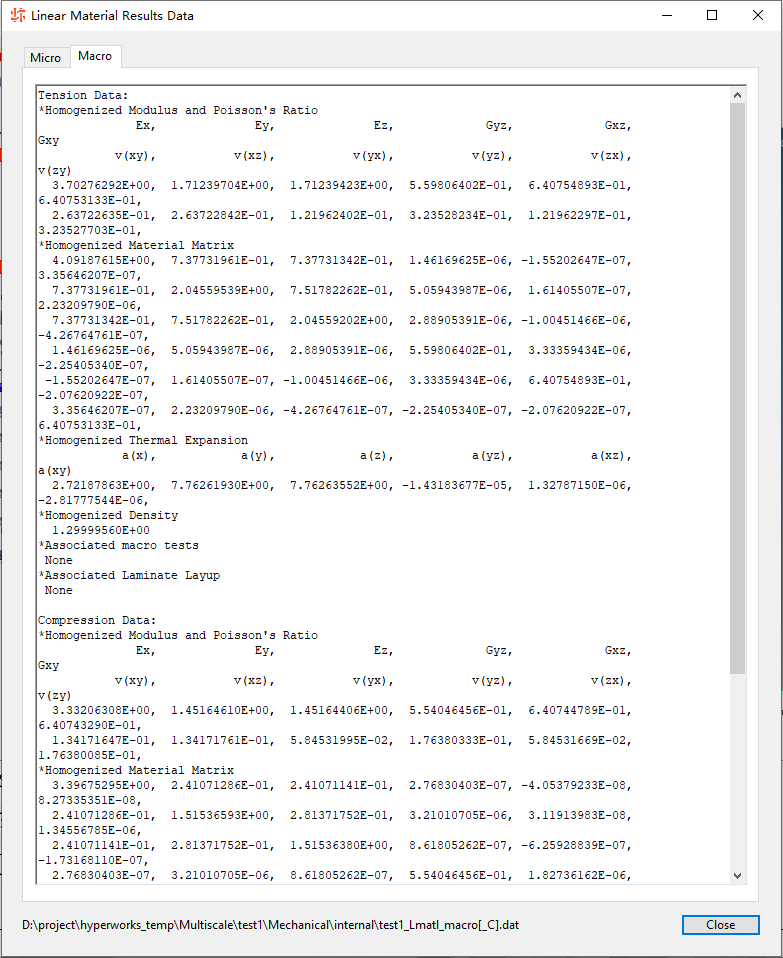
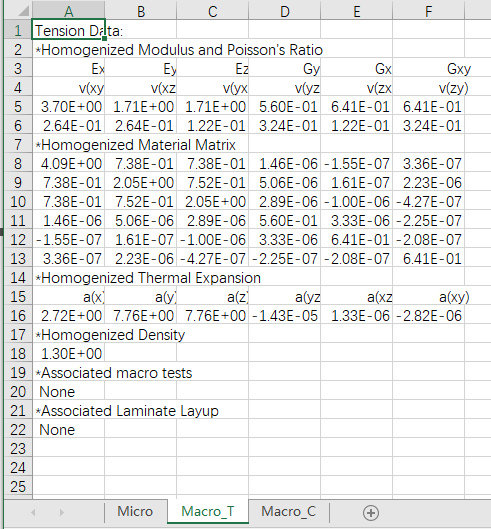
点击Excel可以将等效参数导出到Excel。点击HyperView可以打开HyperView查看OptiStruct计算的结果。

所以其实就是对这个单胞模型做了6个工况的加载,求出了各向异性的等效材料参数。
查看相关目录,可以看到一个.fem文件,是我们刚才看到的OptiStruct输入网格文件,其中没有材料参数。两个.dat文件,两个.hwascii文件。这其中,.hwascii文件可以结合fem文件,用HyperView一起打开,就是上面显示的结果。其实就是以ASCII文本编码输出的结果文件。
后缀有_C的文件指的是压缩工况。从HyperView的结果中可以看出,虽然加载工况是一样的,但末尾带_C的文件使用的是压缩情况下的材料参数。
所以,据我猜测,其实MDS软件里面根本没有实现一个真正的“拉压不同”本构模型。它只是分别使用拉伸的弹性模量、泊松比,压缩的弹性模量、泊松比作为线弹性材料,计算出了拉伸、压缩时的两套各向异性材料参数。在这两套参数之间,调节泊松比保证单个介质的剪切模量相同而已。用户在宏观分析输入材料参数时,也只是选择拉伸、压缩其中一种各向异性材料参数进行输入而已。接下来,这些各向异性材料参数,就可以输入进任意有限元仿真软件,进行宏观均质化模型的分析了。
没学会的话,MDS还支持导出为各种求解器的输入文件。例如导出Abaqus 的 .inp文件:
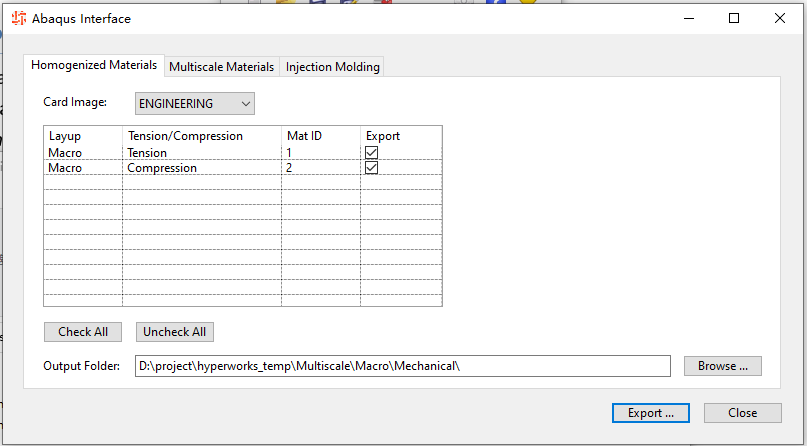
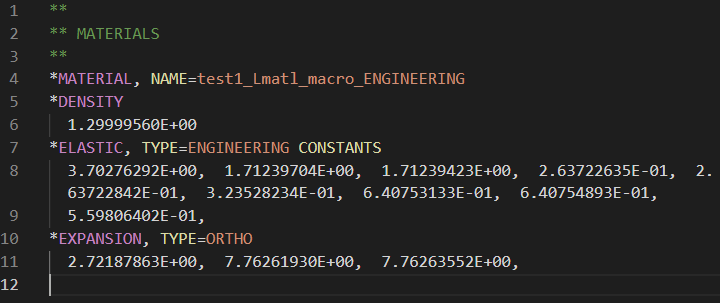
写了这么多……看上去至少在这个基础案例中,这RVE技术实际实现起来其实非常简单。就是建立一个单胞,对它进行三轴正向加载、三轴剪切加载,测出来均质化的各向异性等效材料参数,然后丢进宏观模型分析。这东西其实就相当于在传统求解器上做个二次开发,本质上没啥特别高的技术含量啊。