噪声系数在系统中的应用
(1) 噪声系数是什么?
噪声系数的定义是输入信噪比比上输出信噪比,即噪声系数是对信号的SNR下降的程度进行衡量。

其中,Si/So是指输入信号和输出信号的功率幅度;Ni/No是指输入噪声和输出噪声的功率幅度,而这里需要注意一下,噪声系数定义的温度是16.85℃,即290K。这个温度是IEEE标准设置的测量噪声系数的温度。
一般来说,Ni是指来自匹配电阻的热噪声,即:
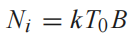
假设系统或者器件的等效噪声温度为Te,那么输出端的噪声功率No为:

而So/Si=G,所以,噪声系数的定义,又可以用下式进行表示:

因此,衡量一个系统或者器件的噪声性能的时候,可以用噪声系数,也可以用等效噪声温度来表示,两者之间有一对一的关系。
(2) 噪声系数和灵敏度之间的关系
可以看到,在噪声系数的定义公式中,Si对应的是输入信号的功率。
链路中的器件,比如放大器等,都有自己标称的噪声系数指标。因此,我们在接收系统设计的阶段,可以通过链路预算,计算出链路所对应的噪声系数。
当输出信噪比So/No为基带解调门限的时候,代入噪声系数和输入噪声功率值,求得的Si,即是灵敏度。
(3) ADC的性能与噪声系数的关系
在评估ADC的性能的时候,也会经常把ADC的SNR指标,或者NSD(噪声频谱密度)指标,换算成噪声系数。
当多个器件级联时,其对应的级联等效噪声温度和噪声系数分别为:

如果把ADC前面的电路整体看成一个器件,ADC看成一个器件,那么:
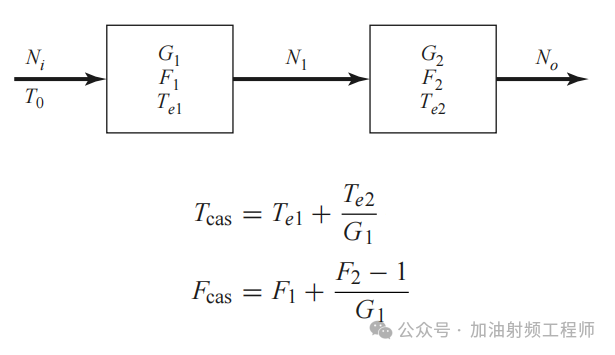
在换算出ADC的噪声系数以后,我们就可以根据整体级联噪声系数的要求,来计算出前级链路所需要的增益和噪声系数,以此作为器件选型的依据。
(4) 噪声系数与发射机宽带噪声的关系
在微波工程中,有这样一个例子。

把dB值转换成线性值 计算级联的噪声系数
计算级联的等效噪声温度
计算输出的噪声
这个例子,虽然题目中说的是接收机,但是也一定程度上模拟了发射机宽带噪声的计算过程。
因为DAC输出的宽带噪声,一般是高于-174dBm/Hz的,而链路中器件的噪声系数定义时,都是假设输入噪声功率为-174dBm/Hz,即对应的T0=290K。而上面的例子,输入噪声温度不是290K,所以就不能直接用噪声系数的公式来计算。因此,上面是做了个换算,用等效噪声温度来计算的。
或者另外一种等效的方法,就是把输入噪声分成两部分,一部分是290K下的热噪声,另一部分是除去第一部分的剩余部分,然后分别计算。

整了一个excel表格,对上面的两种方法,分别算了一下,结果表明,确实是等效的。







