裂缝发育地层井壁坍塌压力求解模型及代码分享
本文摘要:(由ai生成)
本文深入研究了裂缝地层中井壁稳定性问题,特别是弱面对其的影响。针对传统方法忽视软弱结构如裂缝的缺陷,本文基于单一弱面强度理论,分析了裂缝地层的破坏条件,并构建了斜井失稳分析模型。研究发现,裂缝地层具有强度各向异性,斜井井壁应力分布受多种因素控制。通过转换井周应力为主应力表达,可有效评估井壁稳定性。本文为裂缝地层井壁稳定分析提供了新理论和方法,有望降低钻井事故,提升工程安全与效率。井壁稳定分析中常假设岩石为弹性、均质、强度各向同性材料,然后确定维持井壁稳定的临界钻井液密度;然而针对孔洞/裂缝发育的复杂储层,当地层存在一组薄弱面,在较小的钻井液液柱压力下先于岩石本体破坏,但是传统的分析方法忽略了裂缝等软弱结构对井壁稳定影响,常常导致大量钻井事故的发生,在井壁稳定分析中考虑弱面的影响才能解决实际工程问题。
1.裂缝破坏条件
1960年,Jaeger首次提出了单一弱面强度理论,该理论描述了具有一条或一组平行弱面的各向同性岩体的剪切破坏,这是对Mohr-Coulomb准则的推广。因此,根据单一弱面强度理论,裂缝性地层岩石的破坏状态分为两种模式,如图1所示。

图1 含单一弱面碳酸盐岩岩石强度判别准则
(1)当岩体不沿裂缝面破坏,岩体强度等于岩石本体的强度,此时,破坏面与σ1的夹角为∅0=π/4+φ0/2,即岩体强度为:
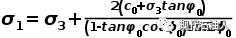 (1)
(1)
(2)当岩体沿裂缝面破坏时,岩体的强度受裂缝面强度控制,即岩体强度为:
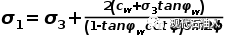 (2)
(2)
岩体沿裂缝面破坏的条件是裂缝面法线与第一主应力方向的夹角∅满足∅1≤∅≤∅2。若∅满足此条件,且应力状态满足式(2)所示的关系,则岩石破坏将沿着裂缝面产生滑移,岩体强度受裂缝面强度控制;若∅不满足此条件,则岩石破坏将沿着∅0=π/4+φ0/2的方向破坏,岩体强度受岩石基体强度控制。其中,∅1和∅2的值可通过式(3)计算。

 (3)
(3)
式中:σ1为最大主应力,MPa;σ3为最小主应力,MPa;cw为碳酸盐岩裂缝面的内聚力,MPa;φw为裂缝面的内摩擦角,(°);c0为岩石本体内聚力,MPa;φ0为岩石本体内摩察角,(°);∅为裂缝面与最大主应力夹角,(°);∅0为岩石本体破坏面与最大主应力的夹角,(°)。
根据单一弱面准则,当cw=10MPa;φw=15°,c0=20MPa和φ0=25°情况下,不同围压下井壁围岩强度如图2所示,说明在裂缝发育地层,强度存在严重的各向异性。
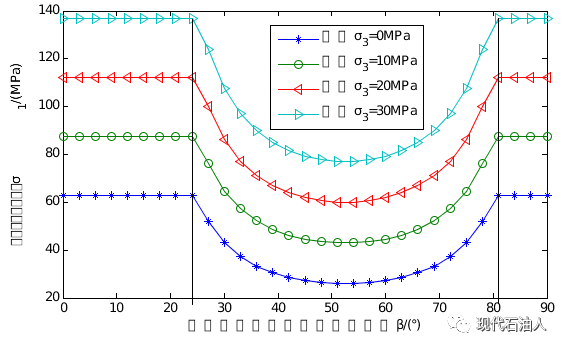
图2 井壁围岩强度与夹角β的关系
2.裂缝地层斜井失稳分析模型
2.1斜井井壁应力分布
井周地应力分布是井壁稳定分析的基础,深部地层受三大主地应力的作用,井周应力受地应力、井斜角α和方位角β控制。假设地层为孔弹性均匀连续介质,斜井井壁处应力分量:
 (4)
(4)
当井斜和方位一定时,井壁应力状态仅是θ的函数,不难看出,σθ和σz随θ变化的增减性一致,因此可在同一位置处取得最大值或最小值,令:
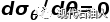 (5)
(5)
求解上式可得:
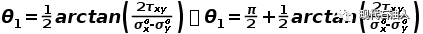 (6)
(6)
井壁周向应力在θ1或θ2处取得极值。在确定井壁应力极值点后,把计算的应力与相应的强度准则对比,可判断井壁稳定与否。
2.2模型求解
由于井壁稳定分析中采用的破坏准则大部分是以主应力来表示,因此,需要将井周应力转换为主应力表达。对于斜井,与直井问题显著不同的是要考虑井斜角α和井斜方位角β,水平最大地应力方位角HA,ω=β-HA,β,HA均以大地坐标系中的北东XX度来表示。假设井壁泥饼完好,不考虑钻井液的渗流效应,斜井柱坐标系中井壁上三大主应力可表示为:
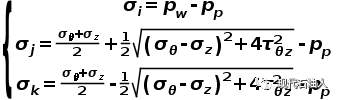 (7)
(7)
井壁主应力的大小,在具体计算中再排序,确定3个主应力的大小顺序。井壁最大主应力σ1的作用面与井眼轴线的交角:
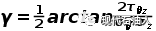 (8)
(8)
式中: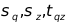 分别表示以斜井井轴为柱坐标系下的切向应力、轴向应力和剪应力。
分别表示以斜井井轴为柱坐标系下的切向应力、轴向应力和剪应力。
在大地坐标系(N,E,Sky)中,弱面地层的走向为北TR东,倾角为DIP,则裂缝面法线的方向矢量n为:
 (9)
(9)
式中:
 (10)
(10)
斜井直角坐标系中井壁最大主应力σ1的方向矢量N在大地坐标系中可表示为:
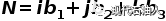 (11)
(11)
式中:
 (12)
(12)
井壁最大主应力与裂缝面法线的夹角∅为:
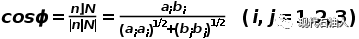 (13)
(13)
首先确定出井壁最大主应力与层理面法线夹角,若式(3)得到的井壁最大主应力与层理面法线夹角满足∅1≤∅≤∅2,则将式(7)得到的三大主应力与式(8)得到的夹角带入式(2)中,求解非线性方程即可得到井眼沿裂缝面剪切破坏的坍塌压力;若不满足,则将式(3)带入式(1)中,求解非线性方程得到井眼未沿裂缝面剪切破坏的坍塌压力;其中,非线性方程的求解采用迭代法求解。
clear;clc;close all;
a=0.492126;%0.15米(m)=0.492126英尺(ft),井眼半径
r=1*a;%井眼周围距离
Alpha_b=20/180*pi; %井眼倾向,°%
h=8000;%井眼深度,单位ft
Sv=0.9;%上覆岩层压力系数,单位psi/ft
Sh1=0.8;%水平最大地应力压力系数
Sh2=0.75;%水平最小压力系数
SV=Sv*h;
SH=Sh1*h;
Sh=Sh2*h;
Pp=0.46;%地层压力系数
PP=Pp*h;
v=0.35;%泊松比
biot=1;%Biot系数
Si=1015;%单位psi,7MPa,本体内聚力
ui=0.58;%本体内摩擦角,30°
Sw=435;%弱面内聚力,3MPa,单位psi
uw=0.466;%弱面内摩擦角,25°
%%
%%%% 原地应力坐标转换到全局坐标(即:大地坐标,Down为Z轴正向,X轴正向指向North,Y正向指向East) ICS 2 GCS %%%%%%%%%
%in-situ stress coordinatesystem (ICS)——global coordinate system (GCS)——坐标转换
Alpha_is=0; %原地应力S_H与全局坐标North轴之间的夹角,°,方位角——stress azimuth,
Belta_is=0; %原地应力S_Z与全局坐标Down轴的夹角,°,井斜角——stress deviation
E_ics2gcs=[cos(Alpha_is)*cos(Belta_is),sin(Alpha_is)*cos(Belta_is),sin(Belta_is);...
-sin(Alpha_is),cos(Alpha_is),0;...
-cos(Alpha_is)*sin(Belta_is),-sin(Alpha_is)*sin(Belta_is),cos(Belta_is)];





