IV储氢气瓶表面最大渗透氢浓度是多少?
摘要
本文研究了在特定工作压力下,IV储氢气瓶在密封空间中的氢气渗透行为。基于布朗运动和扩散理论,我们推导了氢分子在空气中的运动规律,并计算了储氢气瓶表面的氢浓度。随着氢气浓度的增加,浮力效应显著,直至与扩散达到平衡形成准稳态。通过理论计算,我们得出储罐表面的氢气浓度远低于氢气可燃下限,为氢安全工程提供了理论基础。
正文

在特定工作压力条件下,我们将IV储氢气瓶置于一个带有静止空气的密封空间。根据相关理论,我们可以精确预测氢气开始渗透的浓度。储氢气瓶中的氢分子,在布朗运动的作用下,呈现出一种随机而无规律的运动状态。这种布朗运动是受氢分子与空气中其他分子相互碰撞所驱动的。基于爱因斯坦关于布朗运动的定律,我们可以计算出粒子在x轴方向上的平均位移,或者更确切地说,其均方根位移:

其中D为空气中氢的扩散速率(25℃时的速率可以认为是7.79×10-5/m2/s);为时间(s)。当分子在时间t内位移为,面积Ar的IV储氢气瓶表面周围的所有渗透氢分子的体积为Vmix=。该体积中渗透氢的摩尔数为n=JtAr假设氢分子在体积Vmix中均匀分布,则在时间t处,IV储氢气瓶表面的氢体积分数为氢体积与总体积Vx的比率,计算公式为:
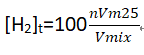
式中,Vm25为25℃下理想气体的摩尔体积(0.0244m3/mol)。该计算公式可以重写为:

随着空气中氢浓度的增加,浮力效应明显增强。因此,IV储氢气瓶表面的氢浓度随时间增加[H2]t&,直至浮力克服氢的扩散的扩散为止,当扩散和浮力相互平衡时,建立准稳态。在密度为air的空气中,密度mix的氢气-空气混合物的浮力运动所适用的牛顿第二定律可以写为F=Mmixa=(air-mix)Vmixg,从力学上讲,物体以加速度a通过距离Lx=at2/2,所以有:

因此,混合物的浮力随时间的位移为:

式中,混合物的密度定义为:

氢气随浮力位移与氢气随扩散位移具有相同的数量级,=,并且处于一下情形时过程达到准稳态:
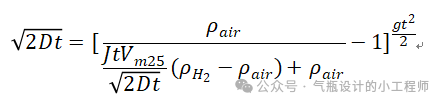
按照SAE J2578(2009),对于下一章节中描述的储氢管和车 库而言,该公式得出储罐容量的渗透率J=1Ncm3/(h·L)(容器内部每升每小时标准立方厘米)的时间为37s(场景1),得出车 库的渗透率J=45Ncm3/(h·L)的时间为16z(场景2)。
在本节的假设条件下,可用式

分别计算出这些特征时储罐表面的氢气浓度为2.4×10-4(体积分数)和1×10-2(体积分数),储罐表面氢浓度的这两个值都远远低于体积分数为4%的氢气可燃下限。《文章来源:氢安全工程基础-机械工业出版社》





