【2017 ATC 优秀论文赏析】基于OptiStruct的双弧形实心碳纤维弹翼铺层优化设计
本文摘要(由AI生成):
本文主要介绍了一种基于OptiStruct的双弧形实心碳纤维弹翼铺层优化设计方法。通过将OptiStruct三级优化设计和等效设计方法相结合,实现了双弧形实心碳纤维弹翼的优化设计,显著提高了弹翼的结构承载能力。文章还介绍了弹翼的几何参数、材料参数、边界与载荷、优化前弹翼初始计算、自由尺寸优化、尺寸优化、顺序优化等步骤,并给出了优化前后的主要参数对比和优化分析与讨论。
基于OptiStruct的双弧形实心碳纤维
弹翼铺层优化设计
孙晓博 李学峰 赵志军 肖和业
张永励 刘宇涛
摘 要:针对于小型战术导弹双弧形实心弹翼碳纤维复合材料铺层优化设计一直是工程中的难点,本文借助于OptiStruct在复合材料优化设计的优势,创新性地将OptiStruct三级优化设计和等效设计方法结合起来,实现了双弧形实心碳纤维弹翼的优化设计,由仿真分析结果表明弹翼碳纤维复合材料铺层优化设计显著提高了弹翼的结构承载能力。
摘 要:针对于小型战术导弹双弧形实心弹翼碳纤维复合材料铺层优化设计一直是工程中的难点,本文借助于OptiStruct在复合材料优化设计的优势,创新性地将OptiStruct三级优化设计和等效设计方法结合起来,实现了双弧形实心碳纤维弹翼的优化设计,由仿真分析结果表明弹翼碳纤维复合材料铺层优化设计显著提高了弹翼的结构承载能力。
1.概述
1.概述
航空航天飞行器结构关键部位复合材料应用的比例被视为飞行器结构先进性的体现。而飞行器复合材料结构的力学性能的影响因素包括:纤维的铺设角度,铺设比例和铺设顺序。通过改善铺层角的参数来调节层压板的泊松比和各个方向的强度,充分发挥复合材料的可设计性。
典型的飞机翼盒式结构的优化在工程上已经研究了很多,也取得了丰硕的科研成果。然而对于双弧形实心的异形结构来说,前缘到后缘非均匀变化,给模型有限元建模带来很大的困难,优化也因为变量的增多使得优化设计更具有挑战性。本文基于工程和学术所取得的科研成果,综合分析双弧形实心碳纤维弹翼的优化设计所应该考虑的难点,提出了将等效设计和OptiStruct相结合的方法来优化碳纤维弹翼的铺层,提高碳纤维弹翼结构的承载能力。
2.有限元模型
2.有限元模型
2.1
几何模型与材料参数
双弧形碳纤维弹翼的几何参数为:翼型NACA0010,翼弦长43mm,弹翼展长165mm。采用T700碳纤维铺设,其性能参数如表2.1所示。本文的坐标系规定是:弹翼展长方向为X轴,翼弦方向为Y轴,Z轴为垂直于XY平面的方向。该碳纤维弹翼初始铺层是:[45/-45/02/902/03/45/-45/02/45/-45/90/0]^s
表2.1 T700材料参数
2.2
边界与载荷
导弹在飞行状态下,弹翼上下翼面承受气动载荷和重力载荷;由于复合材料弹翼相对于全弹质量来讲,其质量可以忽略。本文简化载荷承载方式,有限元分析计算时仅在下翼面施加转化而来的均布压力载荷;本文设计载荷453N,安全系数为1.5,极限载荷为680N。
3.优化前弹翼初始计算
3.优化前弹翼初始计算
静力分析的目的是对双弧形弹翼的翼面应变分布规律进行预测。
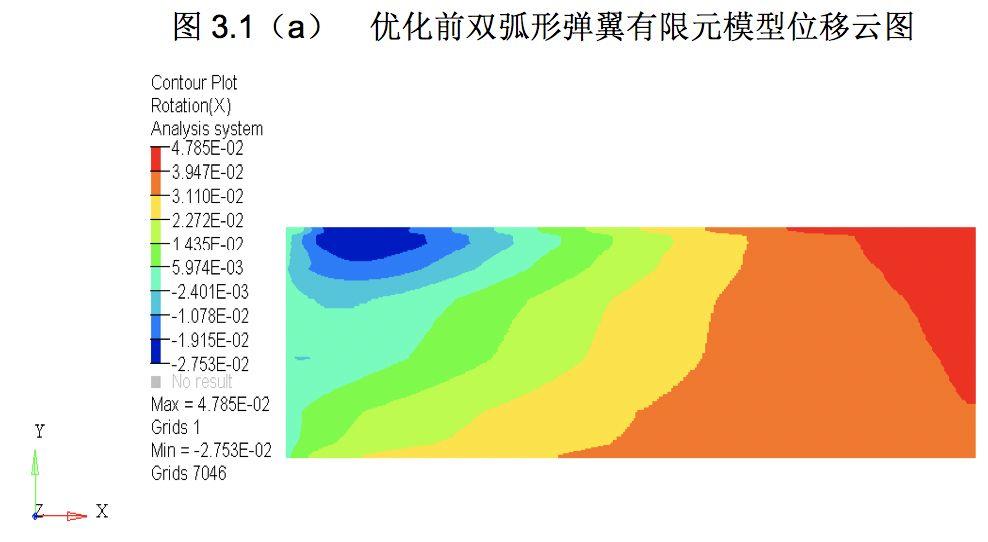
图3.1(a) 优化前双弧形弹翼有限元模型位移云图
图3.1(b) 优化前双弧形弹翼绕X轴的扭转角云图
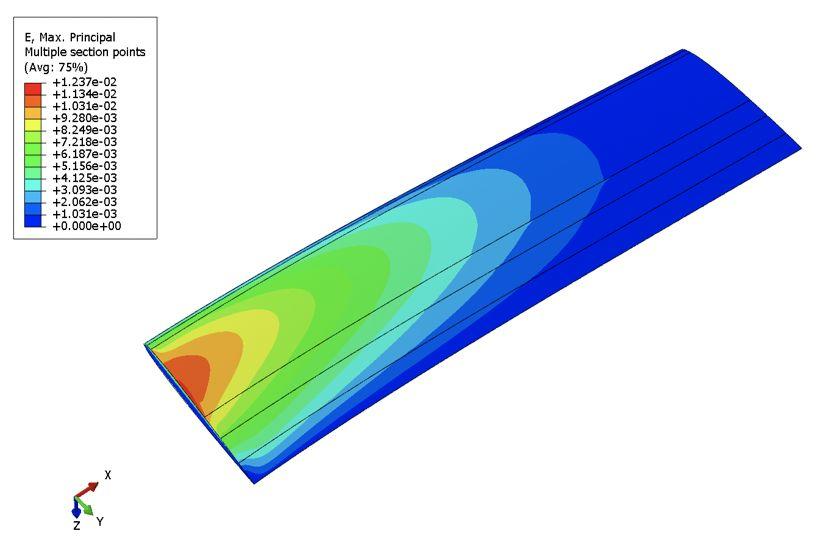
图 3.1(c) 优化前双弧形弹翼模型翼面应变云图
静力分析下双弧形弹翼有限元模型的翼尖挠度、翼尖扭转角和应变计算结果,可以总结以下观点:
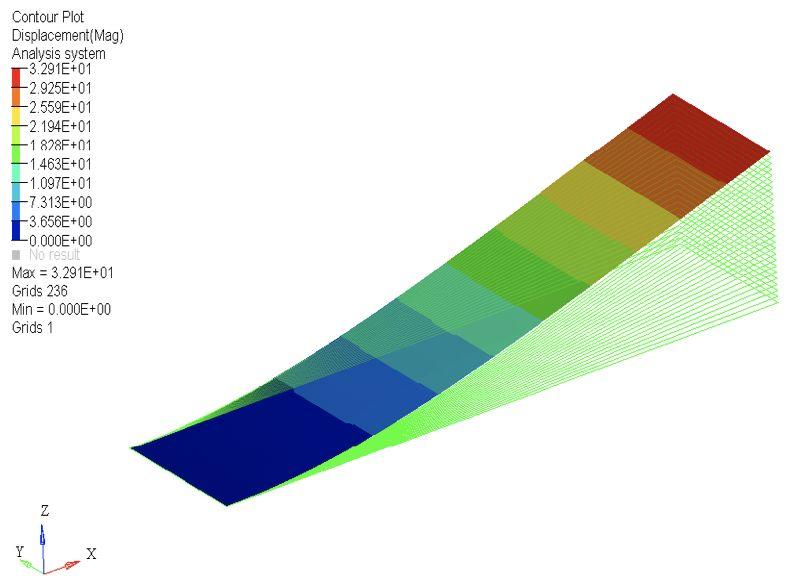
第一:在垂直于翼面的方向的挠度在气动载荷作用下是翼尖最大,由翼尖向翼根逐渐减小;翼尖挠度最大为38.21mm。
第二:以壳单元模拟优化的双弧形弹翼在偏心载荷作用下绕X轴的扭转角是0.04785 rad,对应2.742°。
第三:最大主应变发生在翼面的根部,当然也就是应力最大出现在根部。为了提高弹翼的抗弯曲能力,本文就是要通过优化铺层以减小翼尖挠度和翼面主应变,使得碳纤维弹翼的刚度和强度进一步得以提升。
4.优化设计
4.优化设计
考虑到双弧形碳纤维弹翼翼型的不规则性使得铺设弹翼层压板的每一铺层的尺寸都不相同,同时受限于OptiStruct优化软件模块的限制,我们几乎很难建立一个实体铺层的弹翼,在预定的0.125mm厚度单向板前提下来优化复合材料每一铺层的角度和顺序。本文的研究工作主要是优化双弧形碳纤维复合材料弹翼结构的铺层角度、铺层大小和铺层顺序,使得碳纤维弹翼在多边界和多约束状况下的结构力学性能最优。
基于以上所提出的双弧形复合材料弹翼优化设计的技术难点,本文创新性地提出了“等效设计法”来优化双弧形复合材料弹翼的铺层。本文思路是以尺寸为165*43*4.25(mm)等效复合材料层压板通过放大设计载荷和减小翼尖挠度与翼面主应变来优化复合材料铺层的角度和顺序。图4.1演示了本文优化思路和方法。
图4.1 双弧形复合材料优化流程
4.1
自由尺寸优化
自由尺寸优化设计约束:结构响应约束翼尖位移不大于25mm;
制造工艺约束:单层板铺设厚度0.125mm;0度铺层百分比不小于50%;其余角度铺层百分比不大于30%;层压板厚度最大4.25mm;45和-45铺层成对出现。
自由尺寸优化设计目标:应变能最小化。
自由尺寸优化之后,等效层压板的厚度云图、位移云图和应变云图如下图4.2(a-c)所示,经过分析,我们可以看出:
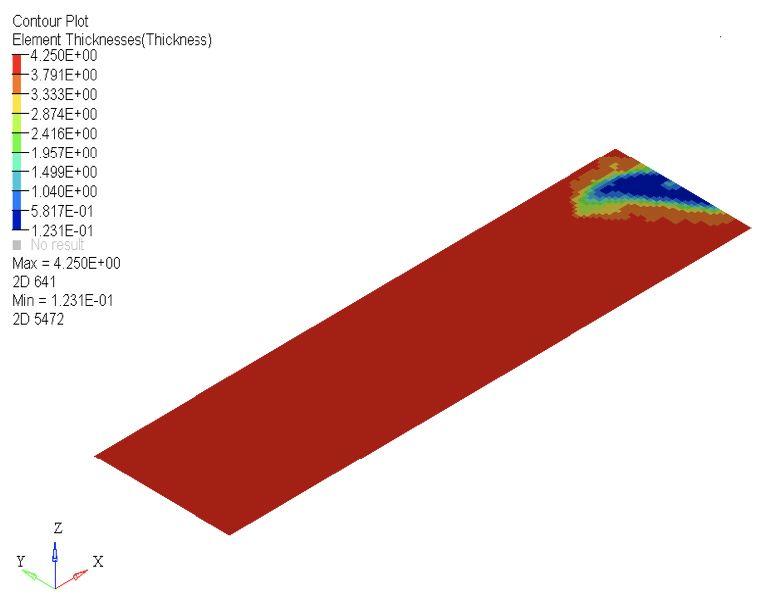
图4.2(a) 自由尺寸优化后单元厚度分布云图
图4.2(b) 自由尺寸优化后的位移云图
图4.2(c) 自由尺寸优化后的应变云图
自由尺寸优化设计之后,等效弹翼生成16个ply的层压板(每一个超级层生成4个同角度的ply)。经过自由尺寸优化之后,层压板形成了不等厚的层压板,这个时候需要进行手工剪裁设计以适应工程制造(HyperWorks14.0 设计了工业自动化剪裁,用户或者制造工程师也可以根据实际情况进行手工剪裁设计)。
自由尺寸优化需要进行剪裁设计。考虑到实心碳纤维弹翼的结构特性属性是铺层单元的铺层是规整的,所以,本文将所有的单元恢复至初始设计的尺寸,即4个超级层单元转化成16个铺层的单层板尺寸是43x165(mm)。从而该弹翼自由尺寸优化的作用则是将超级层的比例进行了优化,也就是我们通过自由尺寸优化得到了每一角度铺层的厚度比例。弹翼尺寸优化设计前,经过剪裁设计后的等效层压板有限元模型如下图4.3所示:
图4.3 自由尺寸优化剪裁后的有限元模型
4.2
尺寸优化
在尺寸优化详细设计阶段,需要对层压板laminate进行整体和局部厚度的约束,如最大和最小层压板厚度;当然,还包括由自由尺寸优化设计转化来的铺层百分比,单层板厚度和对称铺设等工艺制造约束。等效弹翼尺寸优化设计三要素:
尺寸优化设计变量:铺层厚度(16个ply);
尺寸优化设计约束:翼尖挠度不大于28mm,Hoffman失效系数小于1,最大主应变小于7900μƐ。
制造工艺约束:单层板铺设厚度0.125mm;0度百分比不小于50%;其余角度不大于30%;层压板厚度最大4.25mm;45和-45铺层成对出现。
尺寸优化设计目标:应变能最小化。
等效碳纤维层压板尺寸优化设计了位移、失效、应变和应变能四种响应,其中,将位移、失效和应变能响应转化为尺寸优化设计的约束响应,因此应变能最小化就成为了优化目标响应。同时,考虑到弹翼因为拉弯和拉剪等耦合因素造成的翘曲,本文层压板必须设计为均衡对称的层压板;所以在尺寸优化设计阶段我们需要将层压板Laminate的属性从Smear修改为Symmetric Smear,即对称铺层且忽略顺序,因为顺序是最后优化所需的工作。由于尺寸优化阶段的文件要向顺序优化过度,所以需要在control cards设置output为SZTOSH(从尺寸优化到顺序优化)。经过迭代优化计算,图4.4(a~d)为尺寸优化后的结果:
图4.4(a) 尺寸优化厚度分布云图
图4.4(b) 尺寸优化位移云图
图4.4(c) 尺寸优化应变云图
图4.4(d) 尺寸优化失效系数云图
等效碳纤维复合材料层压板尺寸优化后的结构性能大幅度提升,翼尖位移从32.91mm降低到23.67mm,由此可见层压板刚度提升了很多;最大主应变由7961μƐ降到7378μƐ,同时层压板失效系数也远小于1。等效层压板尺寸优化设计后,等效弹翼的结构强度、刚度等技术指标进一步得到提升。
4.3
顺序优化
本文在第二阶段尺寸优化的结果上添加2个工艺约束:第一,最大相同角度铺层不超过4层;第二,最外层铺设±45°铺层。并且,顺序优化阶段的Laminate属性设置为Symmetric,保证优化的铺层顺序为上下对称铺设。基于OptiStruct顺序优化阶段考虑了全局的响应和所有的约束,图4.5(a~c)展示了等效弹翼层压板最终的优化结果:
图4.5(a) 顺序优化后层压板位移云图
图4.5(b) 顺序优化后层压板应变云图
图4.5(c) 顺序优化后层压板失效系数云图
我们分析优化设计的最终结果:翼尖挠度是21.54mm,翼根最大主应变是6951μƐ。
最终我们得到层压板铺层的顺序如图4.6所示。
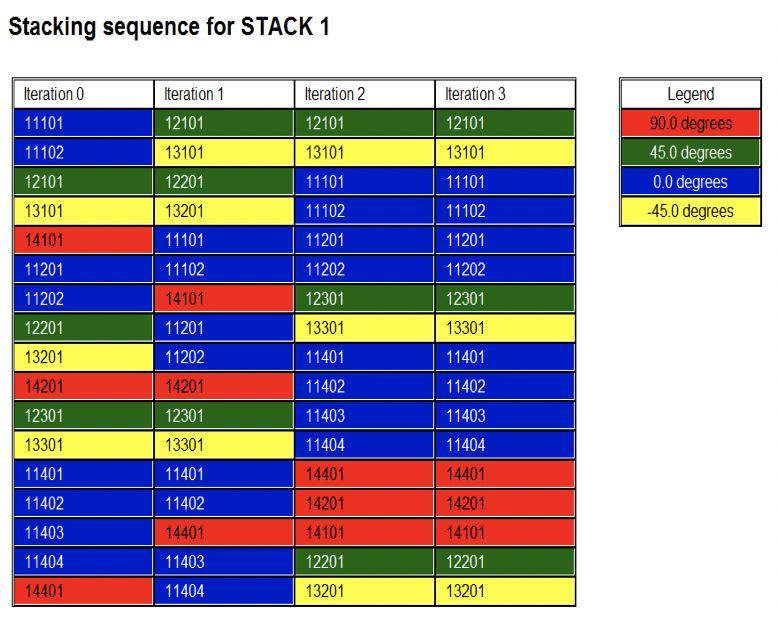
图4.6 等效层压板顺序优化后铺层角度和顺序
最终的铺层书序为:[45/-45/04/45/-45/04/903/45/-45]s。
5.优化分析与讨论
5.优化分析与讨论
该双弧形碳纤维复合材料弹翼采用上下对称铺设,总共34层,每层0.125mm。实际铺层顺序为:[45/-45/04/45/-45/04/903/45/-45]s。
图5.1(a) 优化后双弧形碳纤维弹翼翼尖挠度变形云图
图5.1(b) 优化后双弧形碳纤维弹翼绕X扭转角云图
图5.1(c) 优化后双弧形弹翼翼面主应变云图
图5.1(d) 优化前后双弧形弹翼扭转角云图对比
表5.1是双弧形碳纤维弹翼优化前后的翼尖挠度和翼面主应变的有限元计算结果。它阐述了翼尖挠度从优化前的38.21mm降低至33.71mm,减小幅度11.78%;绕X轴的扭转角位移在数值上没有多大的变化;翼面主应变由12370μƐ减小至11350μƐ,减小幅度8.25%。一阶模态提高了6.96%。对于工程设计领域来讲,这样的优化效果非常显著,从而证明Optistruct三级优化策略在双弧形碳纤维复合材料弹翼上的应用非常成功。
表5.1 双弧形碳纤维弹翼优化前后主要参数对比
分析图5.1(d)所示的双弧形碳纤维弹翼扭转角云图对比,我们从最大的扭转角变化百分比看出相差不大,究其原因是优化前影响扭转角铺层的±45°铺层总数量和优化后的总数量一致,并且都是遵循成对铺设。然而,从整体弹翼优化的角度我们可以发现,优化后弹翼的铺层发生变化,使得优化后和优化前的最大扭转角的区域发生变化,有效地提升了碳纤维弹翼的抗扭转能力。
碳纤维弹翼优化前的翼面最大主应变是12370μƐ这个应变对应的应力非常大,一般的结构部件的复合材料结构很难达到这个强度,也就是说应变不到这个强度铺层就会失效至结构破坏。所以,本文优化设计的目的主要是优化顺序和角度以达到降低结构应力应变和翼尖挠度的效果。本课题的双弧形碳纤维弹翼有限元模型经过三级的优化设计,将翼尖挠度和应变统一降低了11.78%和8.25%,提升了结构抗弯曲能力;同时使得弹翼一阶模态提高6.96%,增强了导弹弹翼的动态特性,使得飞行器结构效率和飞行品质进一步得到提升。
6.总结
6.总结
本文通过对双弧形弹翼为等尺寸碳纤维层压板,基于OptiStruct自由尺寸优化、尺寸优化和顺序优化三步走策略优化设计了双弧形碳纤维弹翼铺层的大小,角度和顺序。经验证优化后的碳纤维弹翼翼尖挠度降低11.78%,翼面应变降低8.25%,一阶模态频率提高6.96%;相对于优化前的双弧形碳纤维弹翼,结构的抗变形能力增强了许多,结构抵抗外激励的能力也增加了。由此证明,等效设计方法和OptiStruct分级优化设计方法的结合使得双弧形碳纤维的综合结构效率提升很多,这种创新性的设计方法对于工程其他复杂截面的复合材料结构铺层优化设计有很好的指导意义和参考价值。、