常见固体材料本构关系
本次推送目录如下:
线弹性各向同性材料
超弹性固体
弹塑性材料
3.1 状态方程
3.2 Johnson-Cook流量模型
3.3 损伤
1. 线弹性各向同性材料
对于各向同性线性弹性材料,应力张量表达式为:

其中λ和μ是Lamé常数。应力张量也经常用流体静力学和偏量部分来表示

体积模量 K 和剪切模量 G 表达式为:
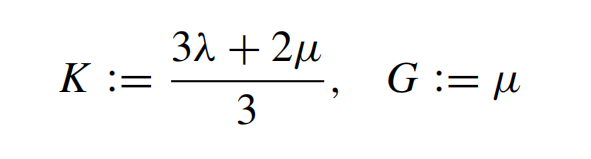
通过下列方程与杨氏模量 E 和泊松比 ν 有关

压力更新的编写方式如下
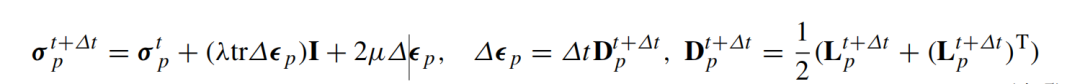
2. 超弹性固体
Neo-Hookean模型是一种各向同性超弹性材料模型,其特征可以用线弹性分析中常见的材料参数来识别
对于该材料模型,第一Piola Kirchhoff应力张量P表示为变形矩阵F和Lamé常数μ和λ的函数,如下所示
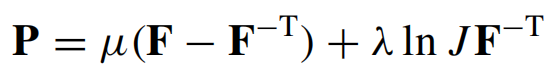

这样的公式便于与总拉格朗日格式一起使用,但J=det F。对于更新的拉格朗日格式,使用柯西应力张量σ更合适。
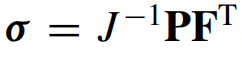
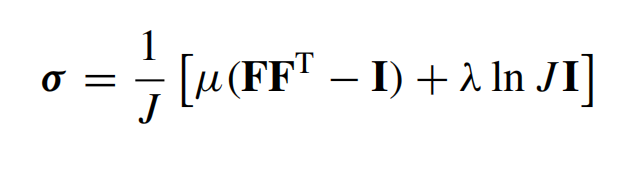
3. 弹塑性材料
材料建模可分为三个领域:体积响应,或压缩阻力(状态方程),变形阻力(本构);以及随着损伤的累积(失效)而承载应力的能力的降低。本节介绍了一个温度相关的次弹性损伤塑性材料模型。该模型适用于大应变和大旋转问题,适用于弹性变形与塑性变形相比可以忽略不计的问题。
处理刚体转动时应力速率的非不变性,刚体运动从应变率中消除,从而从应力率中消除,这是通过首先在旋转R和拉伸U部分中执行F的极性分解来实现的
F = RU 用奇异值分解。
然后从应变速率张量 D 中减去刚体转动,得到非转动应变速率张量
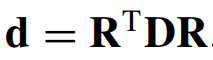
一旦未旋转的应力率被整合到未旋转应力中
,后者被旋转回当前配置,即:
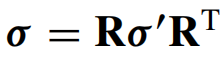
柯西应力张量 σ 表示为各向同性部分,即静水压力之和,和无迹对称偏应力,使用状态方程(EOS)来确定静水压力。
偏差响应是使用塑性流动规则结合屈服条件确定的。这里采用冯-米塞斯屈服条件。此外,当考虑断裂时,使用经典的连续介质损伤力学方法对其进行建模。也就是说,应力张量与损伤变量成线性关系。
总之,模型方程为
1. 应力分解
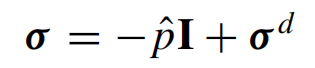
2. 状态方程

3. 应变速率分解

4. 各向同性亚弹性
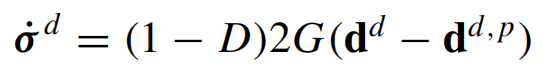
5. von Mises屈服条件

6. 相关塑性流动相关塑性流动
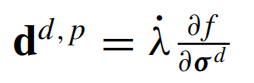
7. Karush-Kuhn-Tucker条件
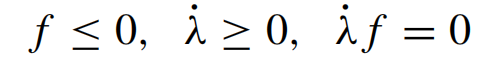
其中G是剪切模量;λ是塑性乘数,dd是未旋转偏应变速率,其中dd,e和dd,p分别是弹性部分和塑性部分;σf为流动应力,
3.1 状态方程
静水压力是使用Mie-Grüneisen EOS确定的,该EOS经过修改以考虑损坏
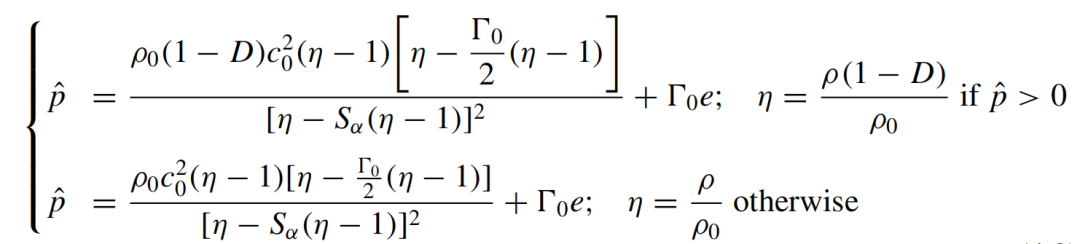
其中c0是声速,0是参考状态下的Grüneisen Gamma。Sα是线性Hugoniot斜率系数。请注意,正压是压缩。
内能 e 写成

其中Cv表示恒定体积下的比热。
对线性状态方程进行了修改,以说明损坏情况,用D表示

其中 K 是体积模量。
3.2 Johnson Cook流量模型
根据Johnson-Cook的流动应力模型,按损伤比例缩放,等效的冯-米塞斯流动应力写为

当 εp 为等效塑性应变时 ε * p 为归一化塑性应变率 a 为屈服应力 b 和 n 为应变硬化参数 c 为应变率参数 m a 为温度系数。这个模型有五个实验确定的参数,可以很好地描述许多金属的响应。
归一化塑性应变率和相应温度 T * 由以下公式给出:
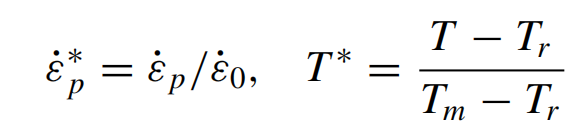
其中,*εp和*ε0分别为塑性应变速率和用户定义的参考塑性应变率;Tr表示基准温度,Tm是基准熔融温度。除非另有说明,*ε0=1.0 s−1。
塑性应变、其速率、温度和损伤的影响是通过相互相乘而耦合的。如果对损坏不感兴趣,只需省略其支架即可。同样,如果不需要热软化,则应跳过相应的括号。温度T可以通过求解热扩散方程来计算,或者它可以简单地从塑性加工中获得。对于高应变速率变形,没有足够的时间进行热传导,因此绝热条件占主导地位,温度升高可计算如下

其中0 < χ ≤1是 Taylor-Quinney 系数,它决定了塑料制品转化为热量的程度。金属常用 χ = 0.9。
3.3 损伤
每个颗粒中的损伤量(D)是使用Johnson Cook损伤模型确定的,该模型广泛用于工程应用
这是一个基于塑性应变局部积累的应变率相关的唯象模型。根据该模型,当累积等效塑性应变达到破坏时的等效应变 εf 时,损伤发生
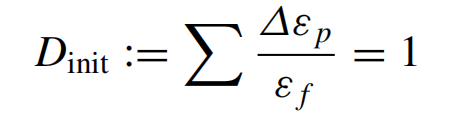
其中Δεp是等效塑性应变增量。失效时的等效应变εf由Johnson Cook的经验方程给出:

其中 D1,... ,D5是五个材料常数 σ =-p/σeq 是应力三轴性。
由于该模型仅描述损伤萌生,因此为了建立完整的断裂现象模型,需要建立损伤演化模型。这里,假设损伤变量由
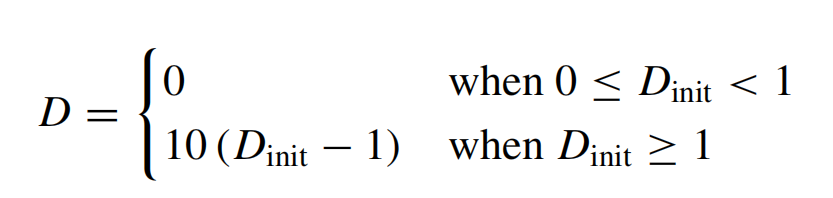
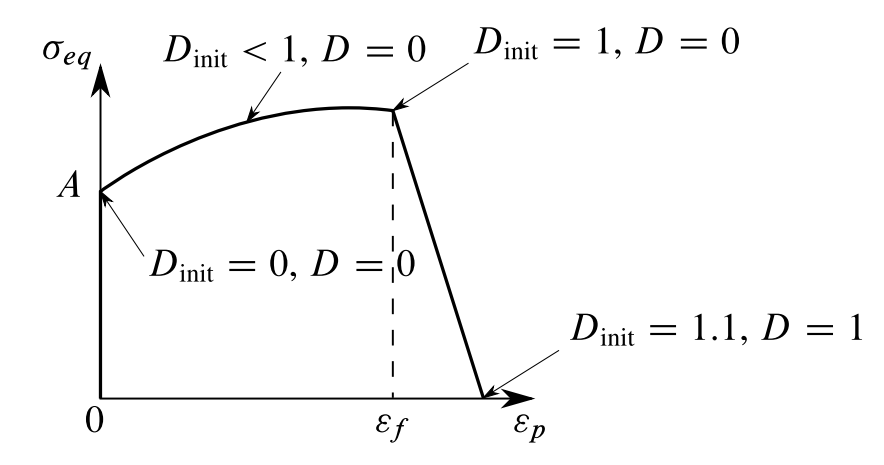
图:典型等效应力-塑性应变曲线示意图,显示了损伤起始变量Dinit和损伤变量D的演变。强调了三点:屈服应力a、损伤起始点Dinit=1和总失效点D=1
即使这种假设影响了损伤传播的细节,也不会改变实现的基本原理。可以使用其他形式的损伤演化。
需要注意的是,这是一个局部损伤模型,通常不适用于损伤建模——结果对网格分辨率敏感




