自适应网格重划分算法:最新研究
文一:

基于自适应网格细化的轴子弦暗物质
摘要:
轴子是假设的粒子,可以解释观测到的暗物质密度和未观测到的中子电偶极矩。世界各地正在进行越来越多的轴子实验室搜索,但由于轴子质量在很大程度上不受约束,这些工作变得困难。如果轴子是在膨胀后产生的,那么有一个独特的质量会产生观测到的暗物质丰度;由于非线性和被称为弦的拓扑缺陷,四十年来准确计算这个质量一直是一个挑战。最近的工作利用大型静态晶格模拟,对轴子质量进行了很大程度上不同的预测,范围从25个微电子三伏特到500多个微电子伏特。在这项工作中,我们表明自适应网格细化模拟比以前使用的静态晶格模拟更适合轴子宇宙学,因为只有串核需要高空间分辨率。使用专用的自适应网格细化模拟,我们在动态范围内获得了超过三个数量级的跳跃,并提供了证据,证明轴子串以标度不变的光谱辐射其能量,精度在~5%以内,从而在(40180)微机电伏特范围内实现了质量预测。

图:模拟快照和插图。

图:瞬时发射光谱。
文二:

Athena++自适应网格细化框架:设计和磁流体动力学求解器
摘要:
介绍了一种用于自适应网格细化计算的新框架的设计和实现。它主要用于天体物理流体动力学,但其灵活的模块化设计使其能够用于各种物理。该框架适用于笛卡尔坐标系和曲线坐标系中的均匀网格和非均匀网格。它采用了一种基于简单设计的动态执行模型,称为“任务列表”,通过重叠的通信和计算来提高并行性能,简化了各种物理的包含,甚至实现了涉及不同计算区域中不同物理的多物理模型。我们描述了在这个框架中实现的非相对论和相对论磁流体动力学(MHD)的物理模块。这些模块采用了最初为Athena MHD代码开发的成熟而稳健的算法,并包含了新的扩展:支持曲线坐标、高阶时间积分器、更真实的物理(如一般状态方程),以及可以与超时间步进算法集成的扩散项。这些模块显示出优异的性能和可扩展性,在50多万个线程上的并行效率远远超过80%。源代码已公开。

图:将 MeshBlock (顶部)及其组织标记为四叉树(底部) ,作为二维统一网格计算的示例。
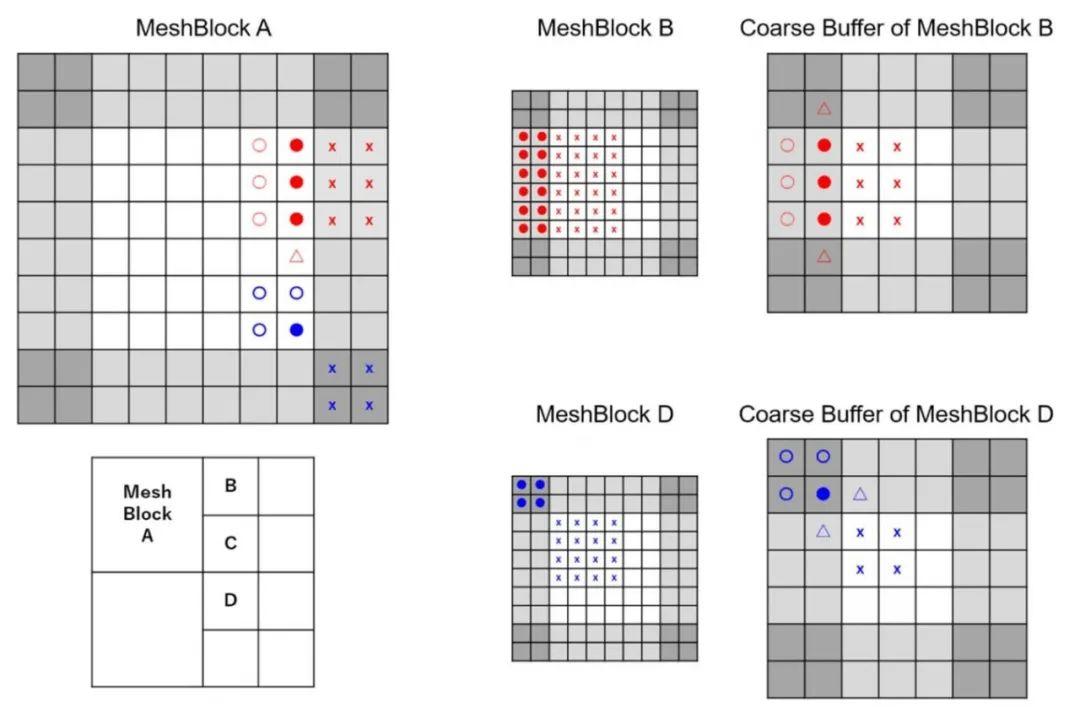
图:左面板: 以单元格为中心的数据(红点)的例子,必须在二维空间中传递给相邻的 MeshBlock。阴影细胞是鬼细胞,与八个相邻的活跃细胞重叠。右面板: 在这个例子中传达的面向中心的磁场(红色箭头)和边缘向中心的电磁场(蓝点)。

图:在各种配置中,在不同细化级别上的网格块之间的单元边缘处的EMF校正的示例。
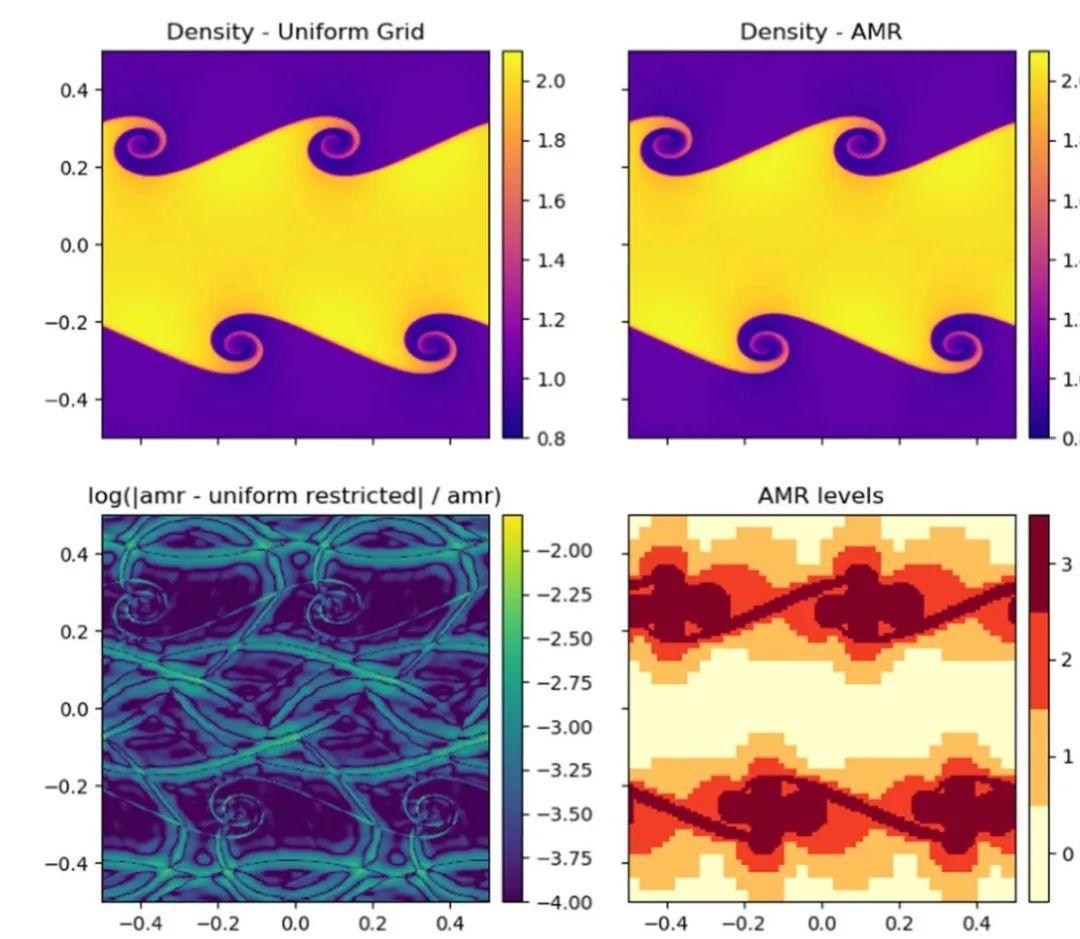
图:.AMR的流体动力学Kelvin-Helmholtz不稳定性试验。左上图显示了使用2048×2048均匀网格在t=1.2时的密度,而右上图是使用4个级别的AMR和82个网格块在相同有效分辨率下的结果.这两者无法区分。左下角显示了均匀网格和AMR运行之间密度的分数差异。右下角面板显示了AMR运行中网格块的分布。

图:Athena++和Dedalus在各种分辨率和时间下解决KHI问题的快照。
文三:

AMReX:用于多物理应用的块结构自适应网格细化
摘要:
块结构自适应网格细化(AMR)为Exascale计算项目在加速器设计、增材制造、天体物理学、燃烧、宇宙学、多相流和风电场建模领域的许多应用提供了时间和空间离散化策略的基础。AMReX是一个软件框架,它为这些和其他AMR应用程序提供了统一的基础设施所需的功能,以便能够有效地利用从笔记本电脑到exascale架构的机器。与均匀网格相比,AMR减少了计算成本和内存占用,同时在复杂的多物理算法中保留了对不同物理过程的准确描述。AMReX支持在简单或复杂几何结构中求解偏微分方程组的算法,以及使用粒子和/或粒子-网格运算来表示组件物理过程的算法。在本文中,我们将讨论AMReX框架的核心元素,如数据容器和迭代器,以及满足应用程序项目需求的几种专门操作。此外,我们将强调AMReX团队正在追求的策略,即在一系列基于加速器的体系结构中为各种不同的应用程序实现高性能代码。

图:化学循环反应器几何结构的网格修剪。此处显示的是嵌入的边界几何图形和级别为0的单个网格,用于相对粗略的模拟。由MFiX Exa团队提供。
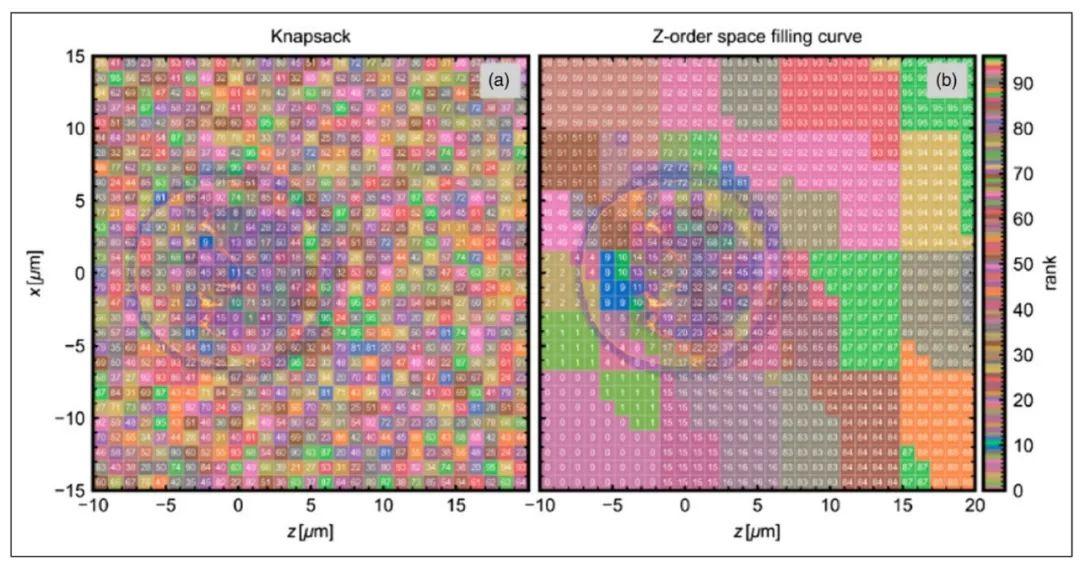
图:比较背包负载平衡算法(左)和皮亚诺曲线(右)的数据分布。

图:异步I/O可能的MPI实现的弱伸缩性研究
文四:

基于水平集方法的自适应网格细化全尺寸三维结构拓扑优化
摘要:
我们提出了一个用于全尺寸三维结构拓扑优化(TO)的并行分布式开源框架。这可以通过采用基于反应-扩散方程(RDE)的水平集方法,将并行计算和网格自适应技术适当结合来实现。离散化和优化隐式定义的曲面(级别集界面)的网格自适应性可以使我们获得具有高分辨率和清晰边界的最佳解决方案。我们的框架可以很容易地扩展到设计具有复杂几何形状的真实世界工程产品,并且可以有效地对由贴体四面体网格表示的优化结构进行后处理。此外,所提出的优化算法可以在一定程度上减轻对初始猜测和网格分辨率的依赖。我们的数值实现使用FreeFEM进行有限元分析(FEA),使用PETSc进行分布式线性代数,使用Mmg进行网格自适应。几个数字例子和3D打印的原型支持这些显著的特征。

图:水平集函数 φ (x)与特征函数 χ 的示意图

图:受刘等人启发的鸟喙实例。

图:二维悬臂梁的设计结果

图:使用自适应网格的三维悬臂梁的设计结果,从左到右依次为:等轴测视图、俯视图、侧视图和后视图。
文五:

用于离散几何组件拓扑优化的自适应网格细化
摘要:
本文介绍了一种自适应网格细化(AMR)策略,用于使用几何投影方法对由离散几何组件组成的结构进行拓扑优化。由诸如杆和板的几何形状制成的实际结构通常相对于它们所占据的设计区域的体积表现出低的体积分数。为了保持准确的分析并确保几何投影中明确定义的灵敏度,要求元素大小小于每个组件的最小尺寸。对于低体积分数的结构,这导致具有大量单元的有限元网格。为了提高分析和优化的效率,我们提出了一种策略,通过在几何组件上设置更精细的网格,并远离它们设置更粗糙的网格,自适应地细化网格并减少元素数量。细化指标非常自然地来源于几何投影,因此易于实现。我们通过对由杆和板制成的最小柔度和应力约束结构的设计进行拓扑优化,证明了所提出的AMR方法的有效性。

图:实心杆在均匀有限元网格上的几何投影。

图:基于有效密度的单构件网格细化。顶级: 第一级细化; 底级: 第二级细化

图:尺寸变量对两级自适应网格细化的影响

图:两条相交钢筋的网格细化和尺寸变量的影响
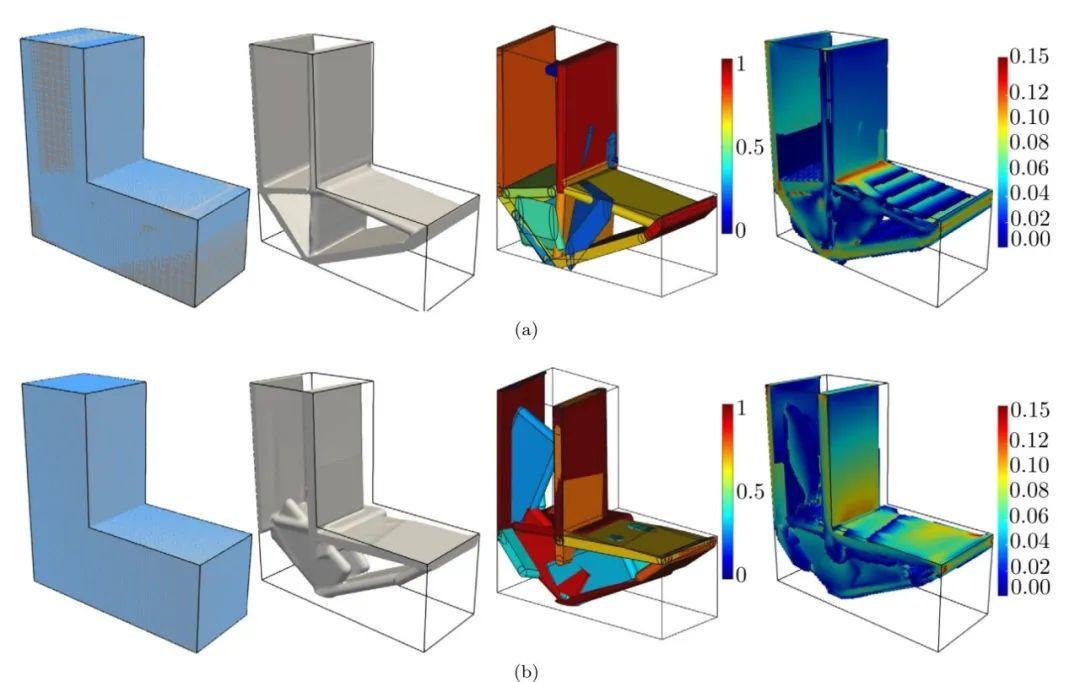
图:优化结果




