技术专题——高性能算法
算法概述
算法v.s计算机算法
其实在没有出现计算机之前,就已经有算法了。简单来说,解决某个问题的方法、步骤都可以称之为算法。

图:算法示意图
例如生活中解决某一个问题的方法,可以简单分为一系列的解决问题步骤。例如,如果要架桥,首先需要筹集资金和人员,其次需要购买原材料和机器设备,然后要开始展开施工,最后还要对造好的大桥展开性能测试。
同样的,对于烹饪,例如:红烧鲫鱼。首先是购买鲫鱼,然后是洗和切,之后在进行其他的相关步骤,如:腌制、加热、装盘等。
图:计算机程序示意图
而在计算机科学领域,用计算机程序解决问题的方法和步骤才是计算机方法。
具体而言,计算机算法包含:输入、计算、输出三个部分,当然,对于某些特定的计算机算法也可以没有输入。
计算机算法有五大特征:
有穷性:一个算法必须是执行有限步骤之后结束;
确切性:每一步都有确切的意义;
可行性:算法中的所有操作都可以通过已经实现的基本操作运算执行有限次来实现;
输入:一个或零个输入,刻画运行对象的基本信息;
输出:一个算法有一个或多个输出,没有输出的算法没有意义。
计算机是如何处理或解决问题的?
计算机中有专门的负责代数和逻辑运算的计算单元——ALU(Arithmetic Logical Unit),是CPU中的代数逻辑计算单元。ALU这一概念的提出最早可追溯到图灵于1936年在论文《论可计算及在密码上的应用》,这标志着人类真正打开了数字电路的计算和逻辑世界大门。
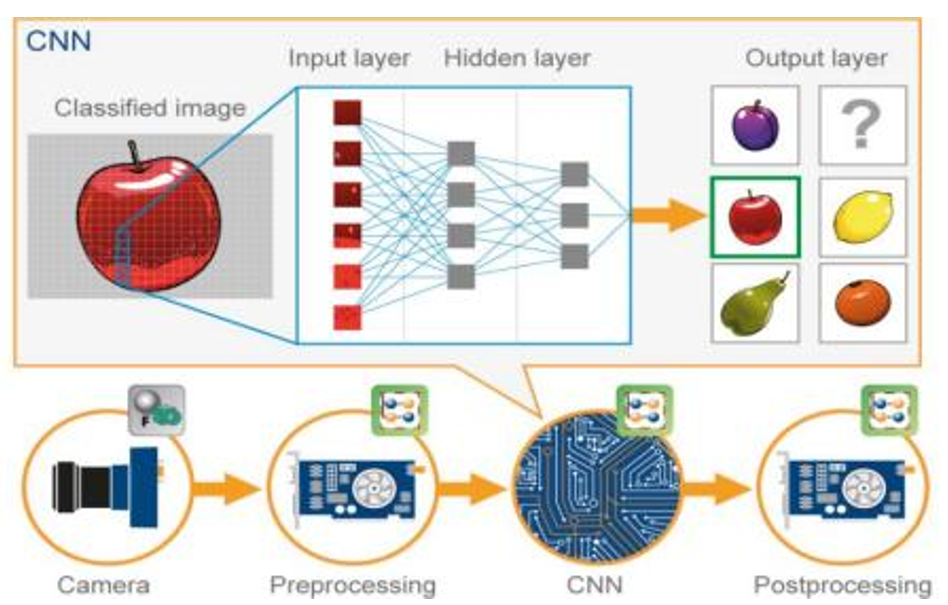
图:代数逻辑运算过程示意图
我们以摄像机处理图片作为例子,简要概述ALU的工作流程和原理。摄像机在取景后,会将图像转化为数字信号存储在摄像机中(Peprocessing,前处理),之后通过CNN(卷积神经网络)处理得到的照片,最后输出(Postprocessing)。这一过程就是图像信息提取,算法设计和输出,而图像识别的过程变成代数和逻辑运算的过程,就会使用到CPU。
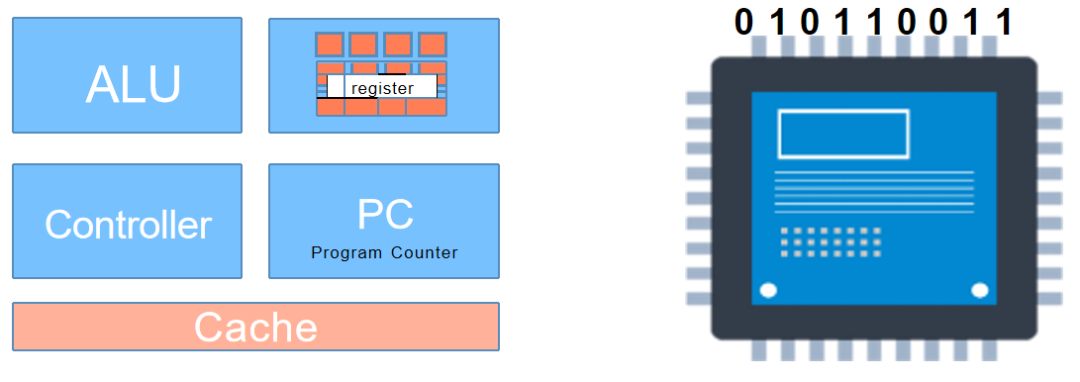
图:CPU和ALU示意图
CPU中包含ALU,缓存(Cache)等一系列的组件,数据会通过CPU不断地传输,完成对数据的输入、计算和输出。所以,计算机算法最终要落脚到代数和逻辑运算上才可以被计算机执行。
计算机算法综述研究

图:计算机应用领域的7个经典问题。
2006年UC Berkeley发表了综述文章《The Landscape of Parallel Computing Research: A View from Berkeley》,对计算机算法的分类和总结,放到现在依旧不过时。
文中提出了计算机应用领域的七个经典问题:
What are the applications?
What are the common kernels of the applications?
What are the hrdware buildblocks?
How to connect them?
How to program the hardware?
How to measure success?
英特尔:识别、挖掘和综合算法
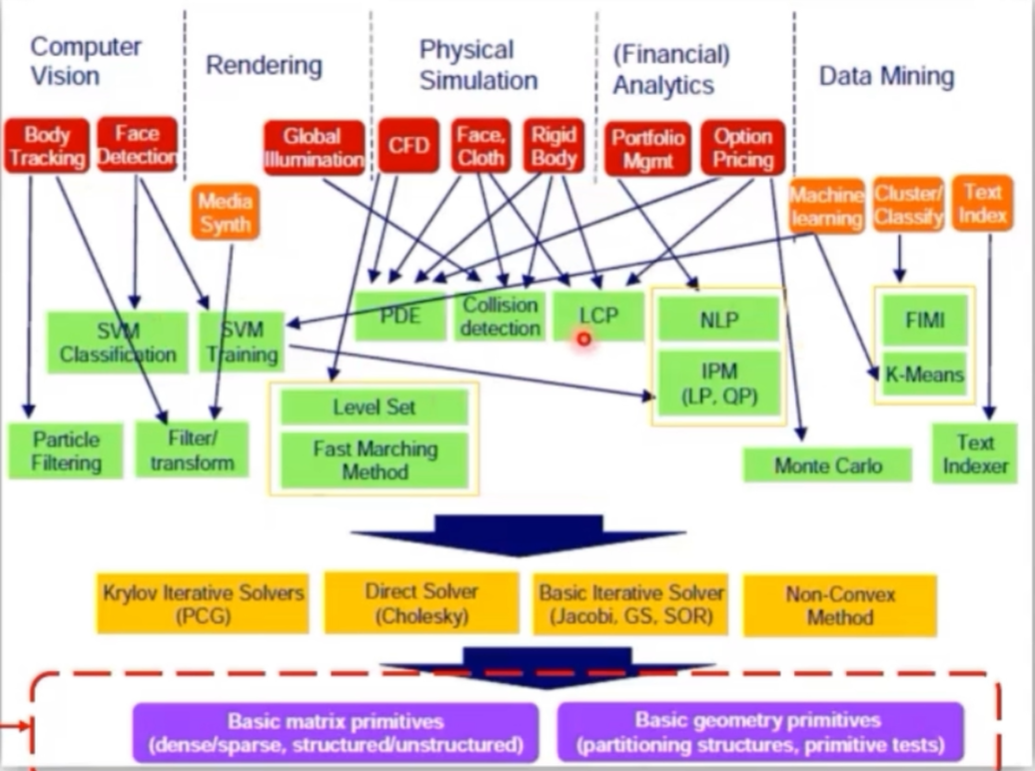
图:算法分类
2005年英特尔的Dubey将计算分为三类——识别Recgnition、挖掘Mining、综合Synthesis。
Recognition:识别是机器学习的一种形式,计算机检查数据并构建该数据的数学模型
Mining:一旦计算机构建了模型,Mining就会搜索网络以查找该模型的实例
Synthesis:合成是指创建新模型,例如在图形中。
RMS的共同计算主题是“对大型复杂数据集的多模态识别和合成”。英特尔相信RMS将在医学、投资、商业、游戏和家庭中找到重要的应用。
在应用方面,计算机应用算法可以被分类为13个“小矮人”:
稠密线性系统:BLAS,GEMM
稀疏线性系统:SPMV,HPCG
谱方法:FFT
多体方法:快速多极子算法
结构化网格:速度快,精度高;例如:jacobi
非结构化网格:适应复杂模型
MapReduce:MC(Monte Carlo)方法
组合逻辑:AES、DES等加密算法
图遍历:Graph500,搜索算法
动态规划
分支限界
图模型
有限状态机
为了测试不同的算法性能,我们可以使用Spec 2006中的科学计算程序做浮点测试的Benchmark。下表展示了部分Spec 2006的计算实例:
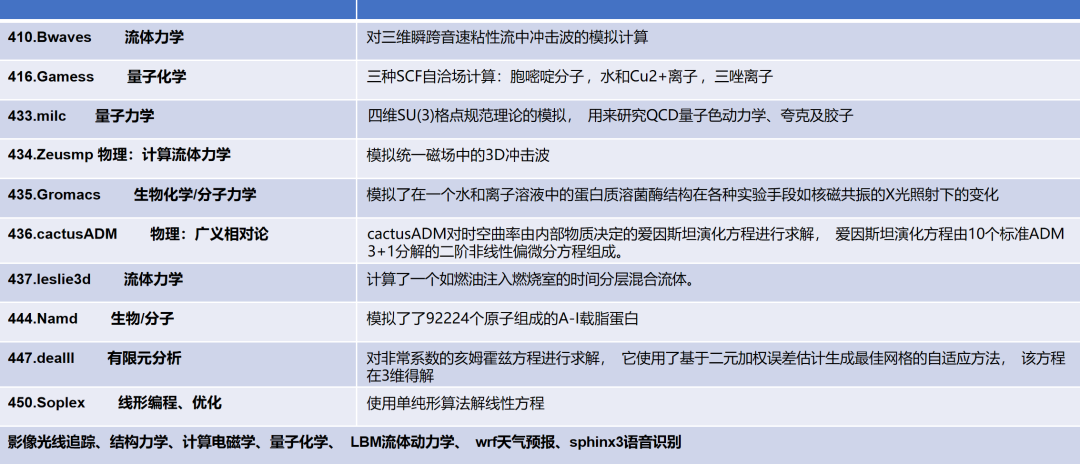
图:Spec 2006计算实例
高性能算法
摩尔定律
摩尔定律是由英特尔 (Intel)创始人之一戈登·摩尔 (Gordon Moore)提出来的。其内容为:当价格不变时,集成电路上可容纳的晶体管数目,约每隔18个月便会增加一倍,性能也将提升一倍。换言之,每一美元所能买到的电脑性能,将每隔18个月翻两倍以上。

图:服务器计算性能随时间的变化
然而,摩尔时代的黄金期就要结束,摩尔极限已经来临。一方面出现了多核的CPU,另一方面计算机的体系结构也呈现出多样化的特点。这就需要根据变化的计算机体系结构提出相对应的计算方法以适应增长的计算量。
程序=数据结构+算法,数据结构是客观对象,算法表示针对客观对象的关系及其处理。
高性能程序=数据结构+算法+体系结构,传统概念上的程序只需关注基本的数据结构及算法流程,只是我们有支撑程序运行的软硬件条件。高性能程序需要关注与体系架构相适应的数据结构,与体系架构相适应的高效算法,并且需要兼顾多体系结构平台的可移植性。

图:GPU示意图

图:FPGA的多核处理器
简而言之,高性能程序就是要能够利用好计算平台的多核处理器和高性能计算显卡,实现对程序的高性能计算。

图:MIT关于摩尔定律和计算性能的综述论文
MIT的科学家们于2020年在Science上发表了关于后摩尔定律时代,提升计算性能的综述论文。该论文提到:
“计算能力的提高可以在很大程度上归功于我们在现代生活中习以为常的许多事情: 25年前比房间大小的计算机更强大的手机,全球近一半的互联网接入,以及强大的超级计算机带来的药物发现。社会已经开始依赖性能随着时间呈指数增长的计算机。”
“计算机性能的大部分提高来自于几十年来计算机部件的小型化,这一趋势是诺贝尔奖获得者物理学家理查德 · 费曼(Richard Feynman)在1959年对美国物理学会(American Physical Society)发表的演讲中所预见的,演讲题目是“底部有足够的空间”。1975年,英特尔创始人戈登 · 摩尔(Gordon Moore)预测了这种小型化趋势的规律性,这种趋势现在被称为摩尔定律(Moore’s law)。直到最近,该定律还是每两年使计算机芯片上的晶体管数量翻一番。”
“不幸的是,作为提高计算机性能的可行方法,半导体微型化正在失去动力ーー在“底层”已经没有多少空间了如果计算能力的增长停滞不前,几乎所有行业的生产力都将面临挑战。尽管如此,计算性能增长的机会仍然存在,特别是在计算技术堆栈的“顶端”: 软件、算法和硬件架构。”
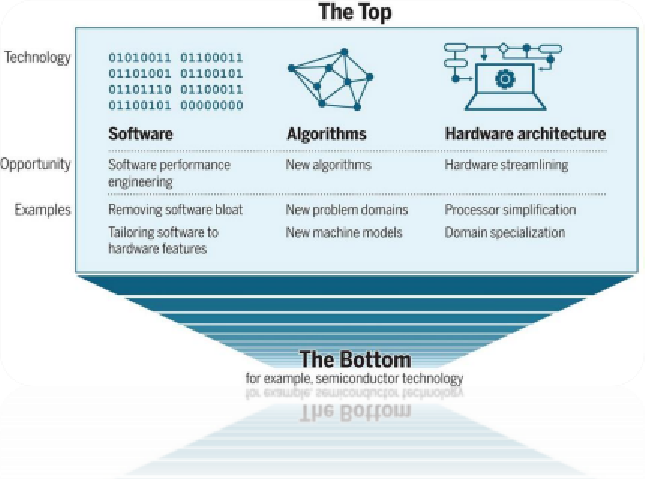
图:计算性能的上限和下限
假设用Python实现一个矩阵乘法的性能是1,那么用C语言重写后性能可以提高50倍,如果再充分挖掘体系结构特性(如循环并行化、访问优化、SIMD等),那么性能甚至可以提高63000倍。
我们为什么需要高性能计算呢?
科学计算:C919和汽车,高铁的研发,通过数值模拟可以大大缩短开发的周期;
军事需求:导弹的弹道计算;
自动驾驶:实现短时间内对数据的大量计算;
AI:大规模复杂神经网络的训练;
机器视觉:图像信号的快速处理
那么,需要什么样的技术才能实现程序移植和优化呢?——程序面向体系结构的全面匹配,以及采用各种性能优化手段
算法可以根据数据的稠密和稀疏程度简单划分为稠密类问题和稀疏类问题。稠密类问题常见于图像处理、深度学习和人工智能领域;稀疏类问题则在科学计算领域较为常见,常见算法有SPMV,HPCG等。
稀疏矩阵向量乘SpMV
稀疏矩阵向量乘法是科学和工程领域的重要核心子程序之一,其原因是在科学计算中其运行过程占据了很大比重的计算时间。例如在使用有限单元法进行结构静力分析时,其约占了70%的运算时间,在迭代求解稀疏线性方程组、代数多重网格算法中约占90%。
另外,稀疏矩阵向量乘法本身的算法特性使得其性能较差。稀疏矩阵向量乘的实现效率较低,一般为计算峰值的10%。这是存储层次的复杂性和矩阵非零元素分布特性共同决定的。由于这些特性使得数据访问的时间和空间局部性和重用性较差。
什么是稀疏矩阵?矩阵中,大量的元素值是0的矩阵,30%甚至更多的元素都是0的矩阵,称为稀疏矩阵。稀疏矩阵和相关运算广泛存在于计算机的各种应用和算法中,比如结构工程中的强度计算,其涉及到的矩阵不仅稀疏,更有对称或正定等特性,甚至计算规模越大,稀疏矩阵性越强(结构静力学的圣维南原理),此外神经网络和机器学习也大量涉及稀疏矩阵的计算。
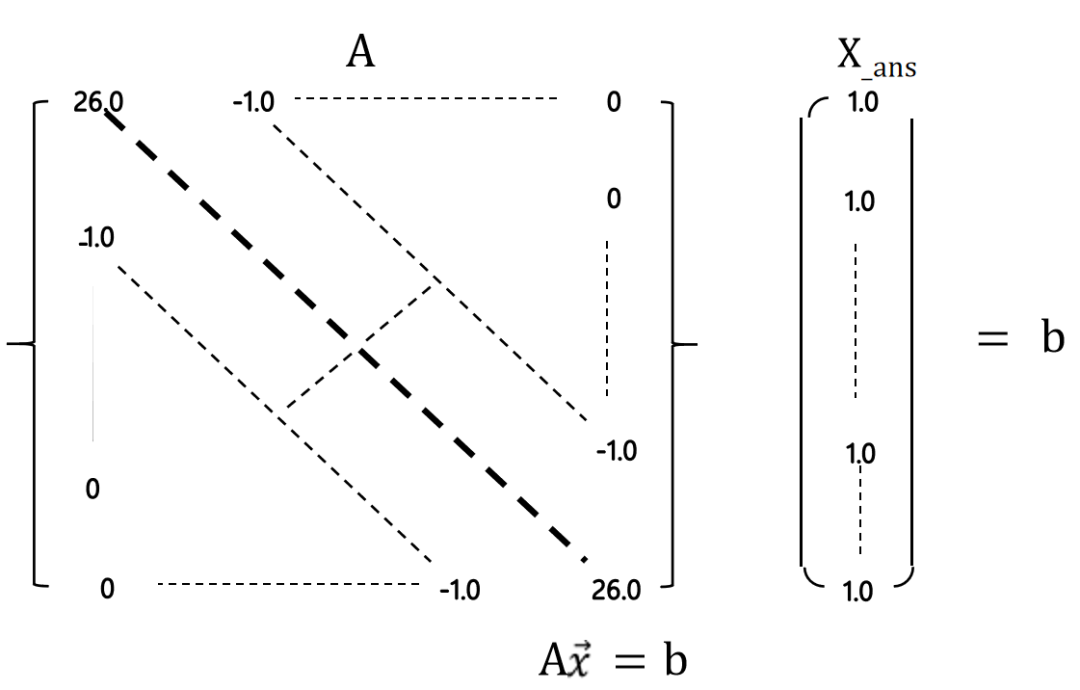
图:稀疏矩阵示意图
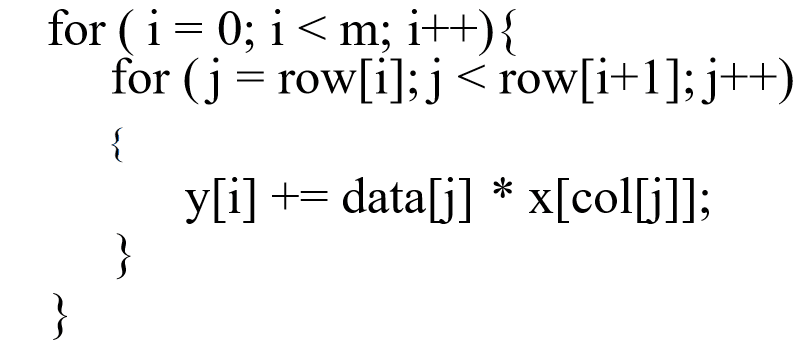
图:SpMV算法示意图(伪代码)
代码中的col[]数组为索引数组——这就引出另外一个问题:稀疏矩阵的存储(或者说数据结构)
稀疏矩阵的数据结构

图:稀疏矩阵的数据分布
稀疏矩阵的存储方法通常是采取——压缩存储。
存储矩阵的一般方法是采用二维数组,其优点是可以随机地访问每一个元素,因而能够容易实现矩阵的各种运算。但对于稀疏矩阵,它通常具有很大的维度,有时甚至大到整个矩阵(零元素)占用了绝大部分内存。采用二维数组的存储方法既浪费大量的存储单元来存放零元素,又要在运算中浪费大量的时间来进行零元素的无效运算。因此必须考虑对稀疏矩阵进行压缩存储(只存储非零元素)。
稀疏矩阵压缩存储的常见方法有:
COO方法:Coordinate Matrix坐标存储格式
CSR方法:Compressed Sparse Row Matrix压缩稀疏行格式
CSC方法:Compressed Sparse Column Matrix压缩稀疏列矩阵
BSR方法:Block Sparse Row Matrix分块压缩稀疏行格式
DIA方法:Diagonal Matrix对角存储格式
稀疏矩阵的COO存储格式
采用三元组(row, col, data)(或称为ijv format)的形式来存储矩阵中非零元素的信息,三个数组row、col和data分别保存非零元素的行下标、列下标与值(一般长度相同),故coo[row[k]][col[k]] = data[k],即矩阵的第row[k]行、第col[k]列的值为data[k]。
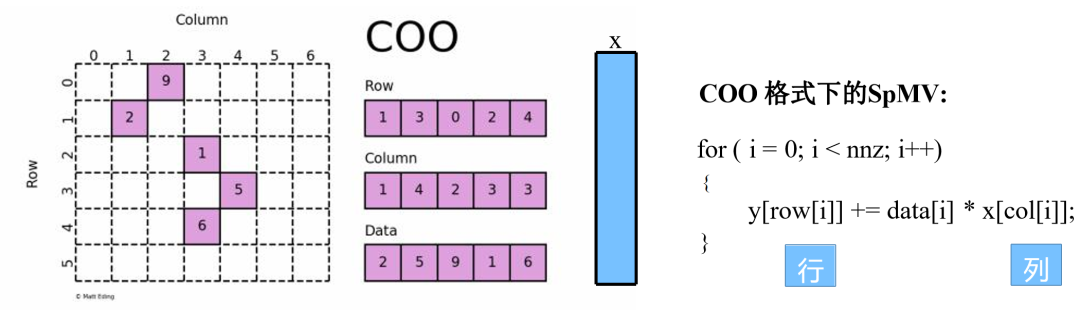
图:COO格式下的SpMV算法
稀疏矩阵的CSR存储格式
csr_matrix是按照行对称矩阵进行压缩的,通过indices,indptr,data来确定矩阵。data表示矩阵中的非零数据,对于第i行而言,该行中非零元素的列索引为indices[indptr[i]:indptr[i+1]]
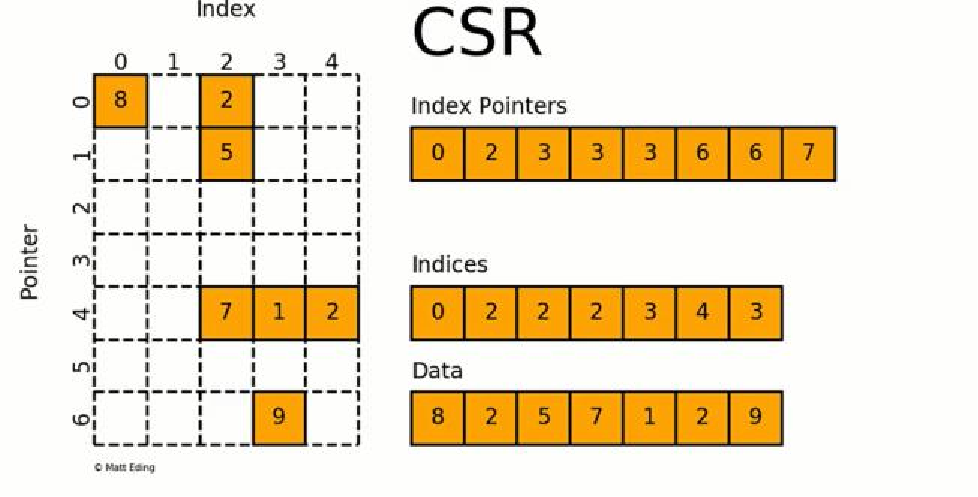
图:CSR存储格式示意图
data:用来存储矩阵中的非零元素的值;
indices:第i个元素记录了data[i]元素的列数;
index pointers:第i个元素记录了前i-1行包含的非零元素的数量
CSR格式和COO的区别:
CSR是将非零元素按照一行一行的顺序压缩,并且存了列号。
COO则无所谓,因为行列编号都存储了。

图:CSR格式下的SpMV算法
上图就是CSR格式下的SpMV算法流程,Row[]即Index Pointers[];col[]即左图的Indices[]。
稀疏矩阵的DIA存储格式
DIA最适合对角矩阵的存储方式,dia_matrix通过两个数组确定:data和offsets。data:对角线元素的值,offsets:第i个offsets是当前第i个对角线和主对角线的距离,data[k:]存储了对应的对角线的全部元素。

图:DIA存储格式示意图
DIA则是存对角线,从主对角线开始,并存下主对角线的偏移量。

图:DIA格式下的SpMV算法
不同格式下稀疏矩阵的存储效率
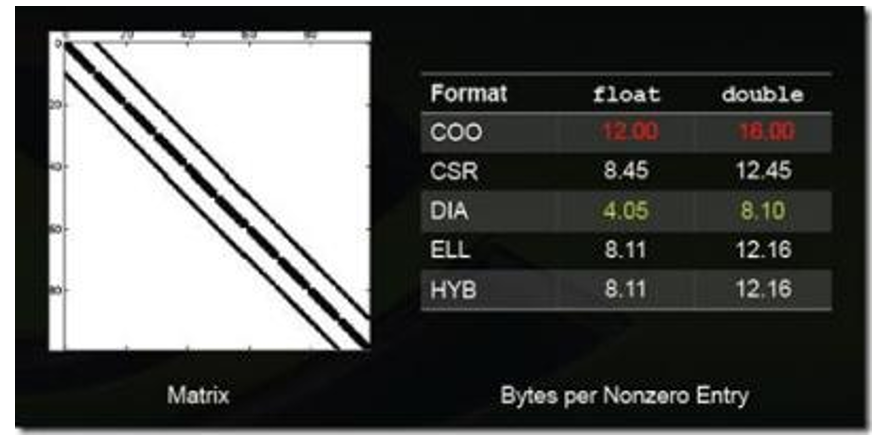
图:稀疏矩阵格式1
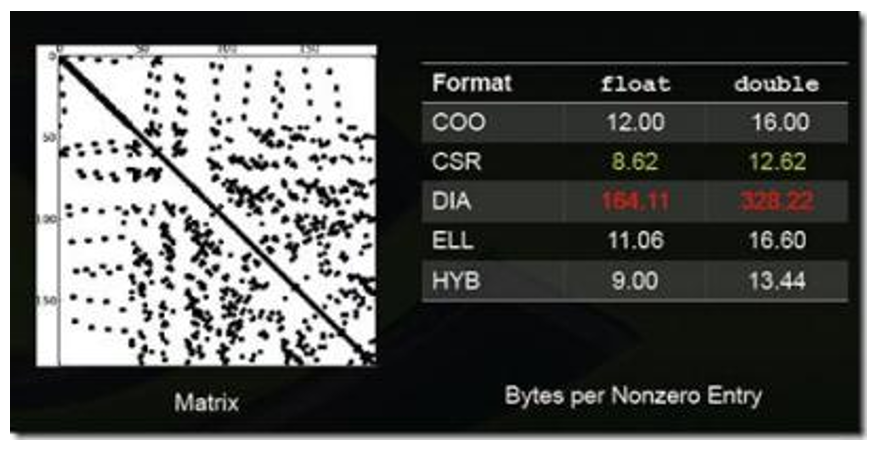
图:稀疏矩阵格式2
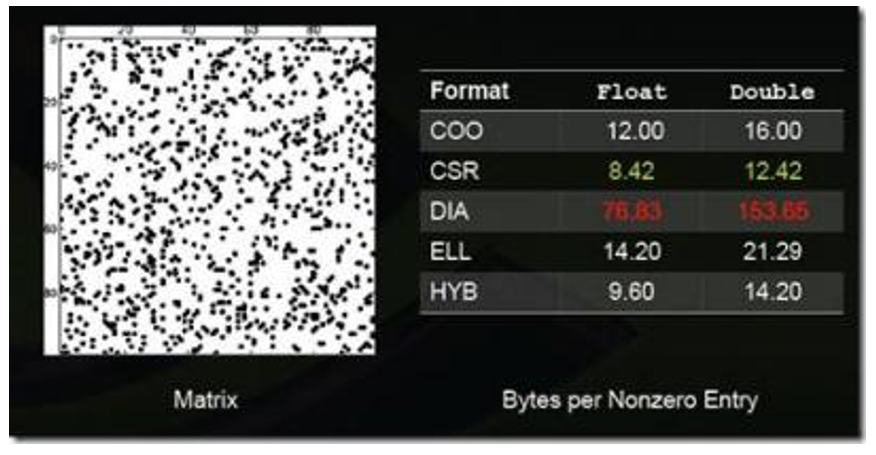
图:稀疏矩阵格式3
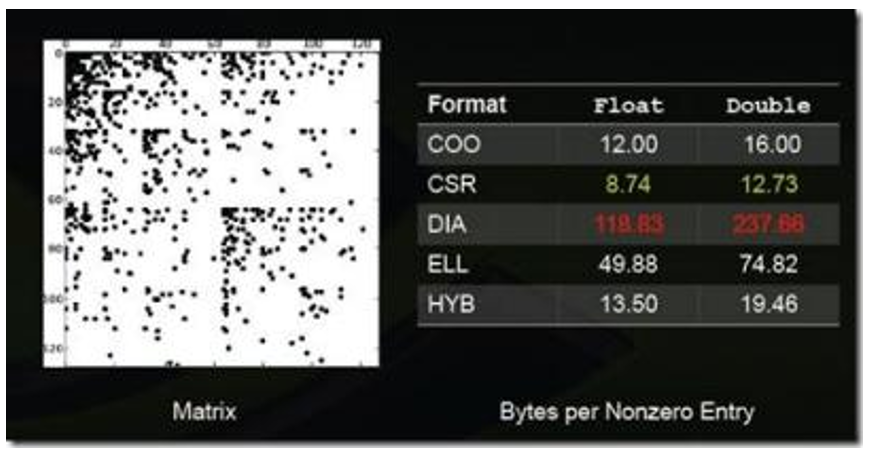
图:稀疏矩阵格式4
上述图列举了一些特殊类型矩阵的存储效率(数值越小说明压缩率越高,即存储效率越高)。
不同的压缩方法适用于不同类型的稀疏矩阵,一般而言,稀疏矩阵的结构性越强适合使用DIA、ELL类的压缩方法;若稀疏矩阵的结构性越弱,适合使用COO、HYB类型的压缩方法。

图:矩阵存储格式和稀疏度之间的关系
SpMV的优化方法
SpMV优化的重点在于改良稀疏矩阵的存储结构,提升稀疏矩阵向量乘时的Cache命中率,并充分利用CPU内部硬件特性,或者多核平台来改善效率。
1. 改良稀疏矩阵的存储格式,提升Cache命中率:
提出新的稀疏矩阵存储格式
自动选择最优存储方式
2. 充分利用CPU内部硬件特性:
向量化技术(SIMD)
管道技术(Pipeline)
预取技术(Prefetch)
3. 多核平台来改善效率:
启发式搜索最优划分块大小
多线程下自动给出划分块大小
SpMV优化方法举例:CSR储存格式下的优化——CSR-SIMD
该存储格式在CSR的基础上,将非零元进一步压缩为可变长的具有连续地址的非零元段,以段的方式对矩阵进行存储。通过这种方式, CSR-SIMD中的每个非零元段都可以进行完全的向量化计算,同时增强了稀疏矩阵A以及向量x的数据局部性,并在不同的平台上取得了很好的性能加速效果。

图:CSR-SIMD存储格式例子
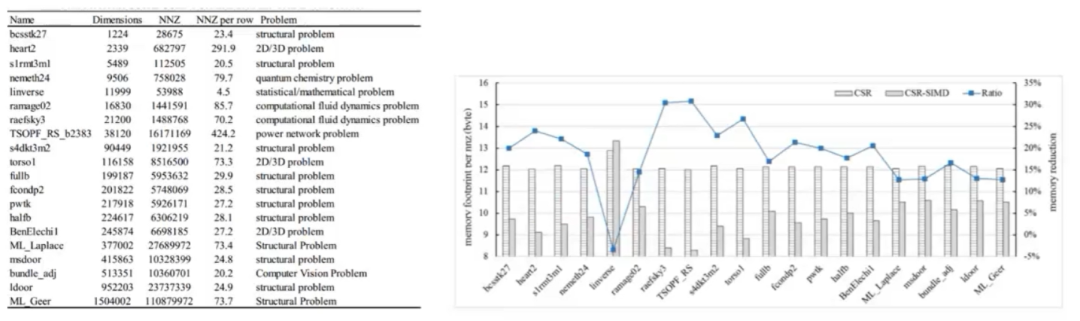
图:CSR-SIMD的优化效果
高性能算法库
算法库基本概念
算法库是计算领域的基础软件库,是发挥硬件算力的基石。
工程领域的问题(EDA、流体流动、天气预报和空气动力学...)和各种物理定律(各种守恒定律、力学定律、电磁学定律等)大部分都可以用偏微分方程(Partial Differential Equation,PDE)描述,在通过计算机求解工程问题时,通常是通过数值计算方法将偏微分方程离散为非线性方程组,再转化为线性方程组进行计算。而方程组的计算就会涉及到算法库。

图:工程问题和科学计算的求解流程
主流的硬件厂商例如Intel、AMD、NAVIDIA等都会为自身的硬件提供优化的算法库。
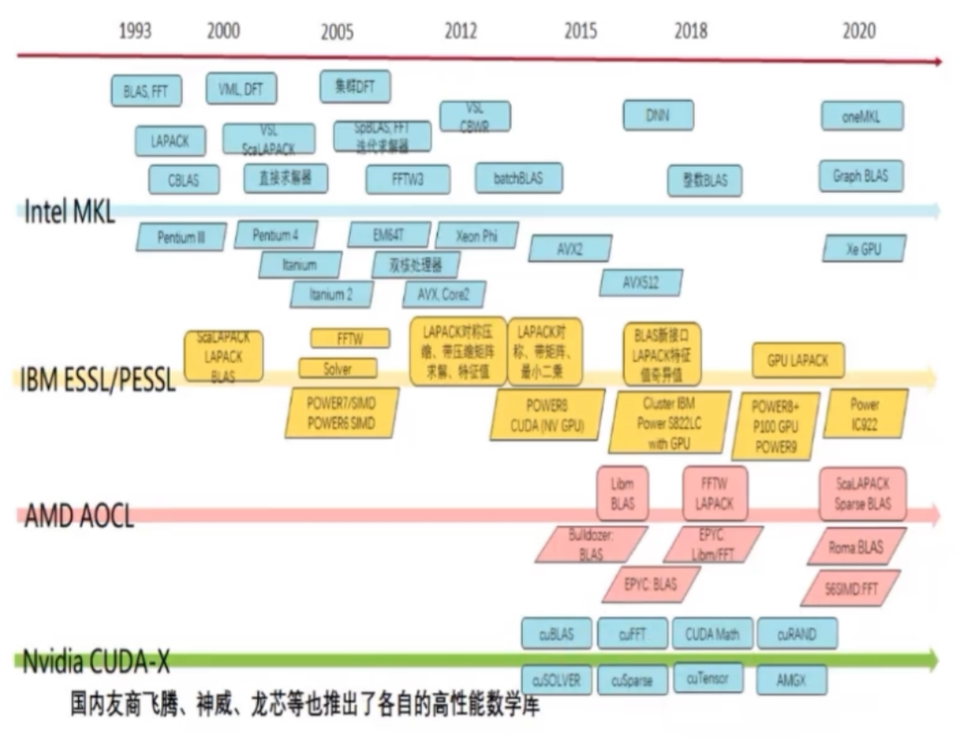
图:常见硬件厂商的算法求解库
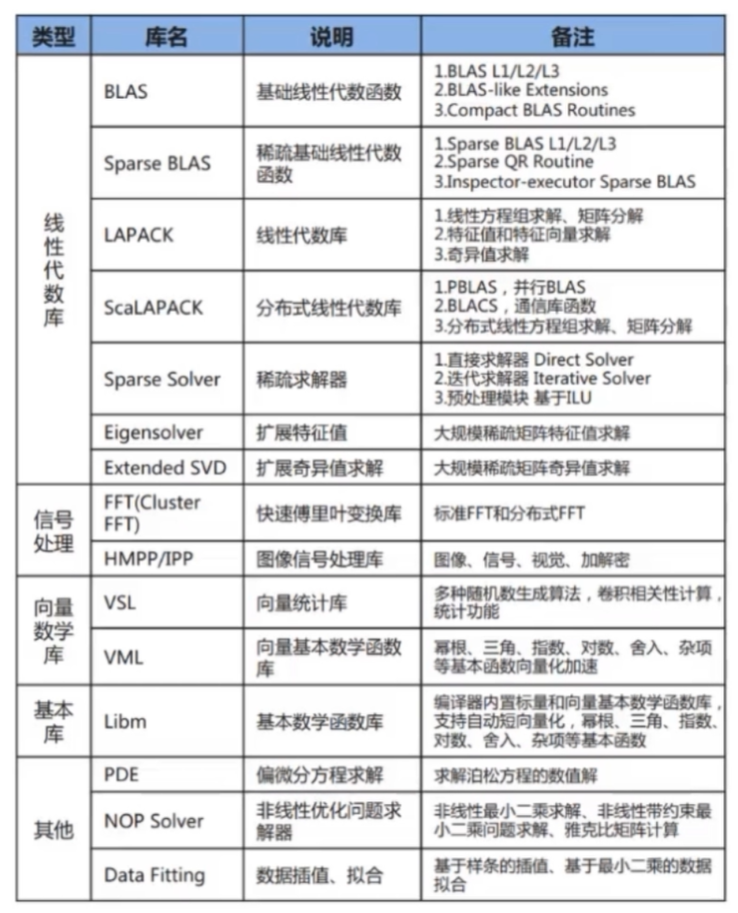
图:常见的算法库介绍
BLAS/LAPACK介绍
BLAS的全称是Basic Linear Algebra Subprograms,中文可以叫做基础线性代数子程序。它定义了一组应用程序接口(API)标准,是一系列初级操作的规范,如向量之间的乘法、矩阵之间的乘法等。
LAPACK(linear algebra package),是著名的线性代数库,也是Netlib用 fortran语言编写的。其底层是BLAS,在此基础上定义了很多矩阵和向量高级运算的函数,如矩阵分解、求逆和求奇异值等。该库的运行效率比BLAS库高。
同时BLAS、LAPACK也是很多库的基础。Intel的MKL和AMD的ACML都是在BLAS的基础上,针对自己特定的CPU平台进行针对性的优化加速。以及NVIDIA针对GPU开发的cuBLAS。

图:BLAS和LAPACK及其他库的依赖关系
PETSc
PETSc(Portable, Extensible Toolkit for Scientific Computation),是美国能源部ODE2000支持开发的20多个ACTS工具箱之一,由Argonne国家实验室Satish Balay等人开发的可移植可扩展科学计算工具箱。主要用于高性能求解偏微分方程组及相关问题。目前PETSc所有消息传递均采用MPI标准实现。
PETSc用C语言开发,遵循面向对象设计的基本特征,用户可以基于PETSc对象灵活开发应用程序。目前,PETSc支持Fortran 77/90、C和C++编写的串行和并行代码。
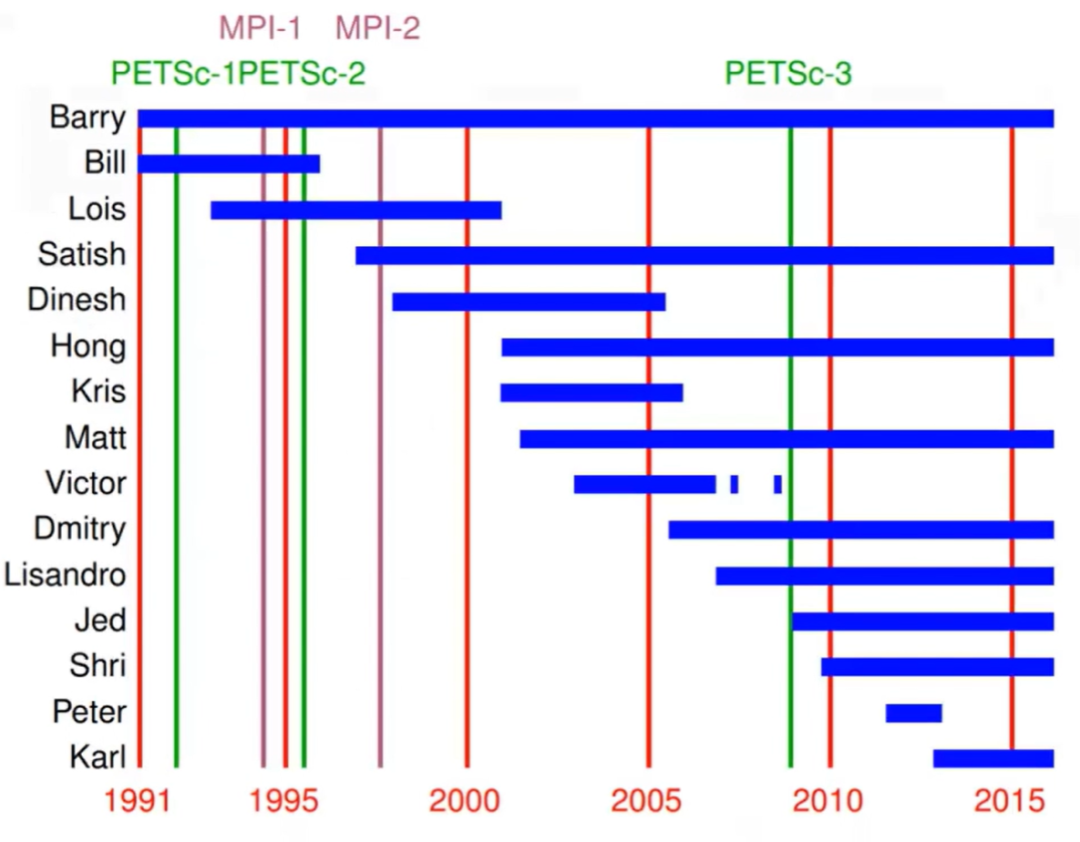
图:PETSc的开发流程
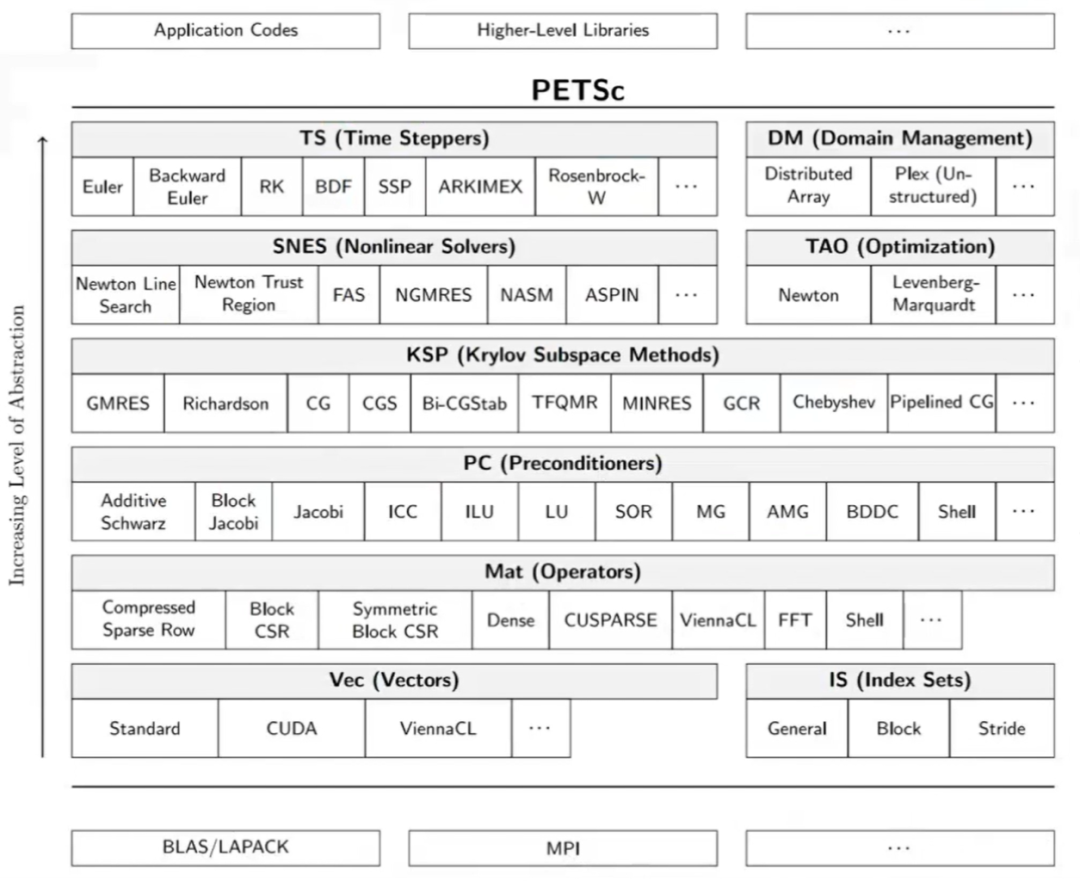
图:PETSc的体系架构
不同于其它微分/代数方程解法器,PETSc 为用户提供了一个通用的高层应用 程序开发平台。基于 PETSc 提供的大量对象和解法库,用户可以灵活地开发 自己的应用程序,还可随意添加和完善某些功能,如为线性方程求解提供预 条件子、为非线性问题的牛顿迭代求解提供雅可比矩阵、 为许多数值应用软 件和数学库提供接口等。下图表示了PETSc 在实现层次上的抽象。
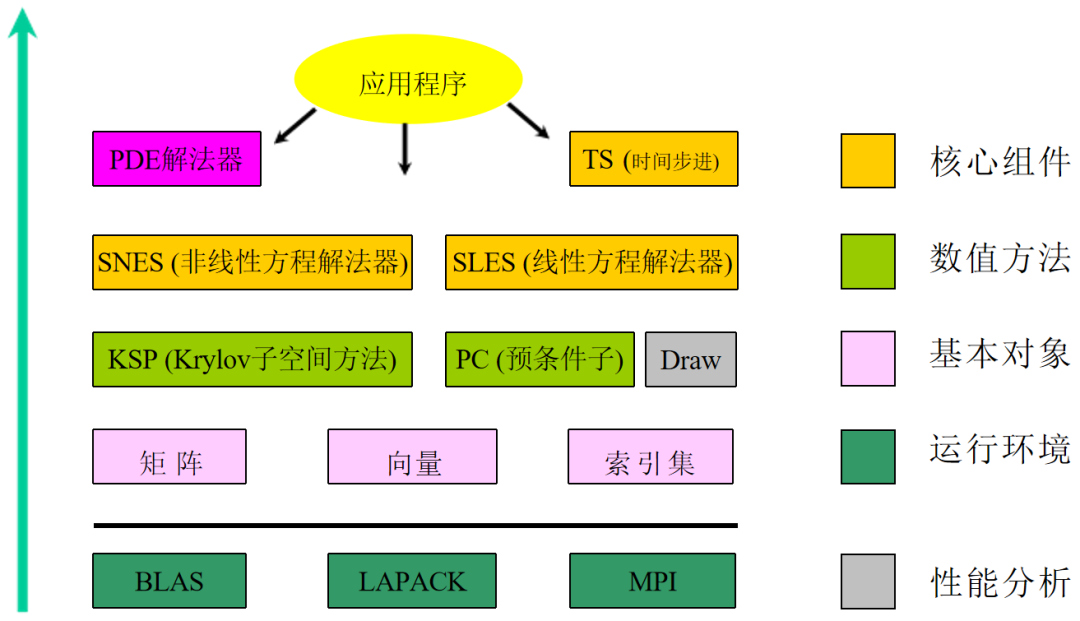
图:PETSc的实现层次
应用程序:用户在PETSc环境下基于PETSc对象和算法库编写的串行或并行应用程序。尽管PETSc程序完全在MPI上实现,但PETSc程序具有固定的框架结构,即有初始化、空间释放和运 行结束等环境运行语句。
PDE解法器:用户基于 PETSc 三个基本算法库(TS、SNES和SLES)构建的偏微方程求解器。但它却不是 PETSc的基本组件之一。
TS:时间步进积分器,用于求解依赖时间或时间演化ODE方程,或依赖时间的离散化PDE方程。对于非时间演化或稳态方程,PETSc 提供了伪时间步进积分器。TS积分器最后依赖线性解法器SLES和非线性解法器SNES实现。PETSc为PVODE提供了接口。另外,TS用法简单方便。
SNES:非线性解法器,为大规模非线性问题提供高效的非精确或拟牛顿迭代解法。SNES依赖 于线性解法器SLES,并采用线性搜索和信赖域方法实现。SNES依赖于雅可比矩阵求解,PETSc既支持用户提供有限差分程序,同时又为用户提供了依赖ADIC等自动微分软件生成的微分程序接口。
SLES:线性解法器,它是 PETSc 的核心部分。PETSc几乎提供了各种高效求解线性方程的解法器,既有串行求解也有并行求解,既有直接法求解也有迭代法求解。对于大规模线性方程组,PETSc提供了大量基于Krylov子空间方法和预条件子的各种成熟而有效的迭代方法,以及其它 通用程序和用户程序的接口。
KSP:PETSc的核心,Krylov子空间方法,广泛涉及Richardson方法,共扼梯度法(CG和BiCG),广义最小残差法(GMRES),最小二乘QR分解(LSQR)等。
PC:预条件子,包括雅可比矩阵,分块雅可比矩阵,SOR/SSOR方法,不完全Cholesky分解,不完全LU分解,可加性Schwartz方法,多重网格预条件子等。
DRAW:应用程序的性能分析和结果显示。
图:KSP的核心算法库
PETSc—PC
为什么需要预处理?
如果 A 的 性 质 不 那 么 好 , 是病态的 (ill- conditioned), 或者主对角线上的元素很 小 ,或者特征值很小 ,那么收敛起来就会 非常慢。
将一个矩阵经过预处理后划分为多个类似结构的矩阵,实现天生并行化。

图:PETSc中预处理方法和对应的指令
PETSc的基本对象是向量(Vectors)、矩阵(Matrices)、索引集(Index Sets)。PETSc向量对象主要用于存储线性方程组的解和右端向量。对于规则的正交网格,PETSc自动对向量进行划分,并通过分布式存储向量(即DA对象)来管理。通过DA对象, 用户可以简单地实现向量的分发、聚集、局部和全局之间的相互映像、边界点的通信等基本操作。DA 对象隐藏了进程之间的通信,用户只需提供全局的向量结构和数值。但对于无结构网格,用户则需通过索引集(即IS对象)来实现向量的分发、聚集、映像、边界点的通信等基本操作。
以下是向量对象的创建、赋值、聚集和释放在PETSc中的对应命令:
VecCreateSeq:创建一个串行的PETSc向量
VecCreateMPI:创建一个并行的PETSc向量
VecCreate:创建一个PETSc向量对象
VecSetSize:设置向量维数
VecSetFromOptions:通过运行参数设置向量类型
VecSet:将一个数值赋给向量的每个元素
VecSetValues:分别给向量的每个元素插入或累加数值
VecAssemblyBegin:启动一个向量的创建
VecAssemblyEnd:完成一个向量的创建
VecDuplicate/VecDuplicateVecs :复 制一个/组向量
VecDestroy/VecDestroyVecs:释放一个/组向量
其他常用的数值算法库





