岩石力学和固体破碎的前沿研究
文一:

结晶塑性与加速循环内聚区耦合模型在织构控制下AA2024合金疲劳裂纹扩展
摘要:
AA2024合金的织构是控制疲劳裂纹扩展(FCP)行为的主要因素,使用晶体塑性(CP)方法可以很好地模拟这种织构特征。此外,由于考虑了损伤演化规律,循环粘性区模型(CCZM)在模拟FCP行为时具有比粘性区模型更高的可靠性。在这项工作中,CP首次与CCZM集成,以预测AA2024合金在织构控制下的FCP行为。为了减少耗时,在XFEM框架下,在这种耦合的CP-CCZM中巧妙地实现了加速策略,试图更快、准确地预测纹理对FCP行为的影响。还进行了FCP和电子背散射衍射(EBSD)实验,为检验该模型的可靠性和准确性提供了参考。研究发现,这种耦合方法在纹理控制下模拟FCP行为时具有很强的能力和鲁棒性。然后利用这种耦合方法模拟了由鞋底强高斯、立方体和黄铜纹理引起的三种典型的FCP特征,并对相应的FCP行为进行了详细的比较分析。

图:FCP的紧凑张力样品的形状(尺寸单位为mm)。

图:多尺度模型(a)CT形状模型和(b)由156个晶粒组成的CP区。
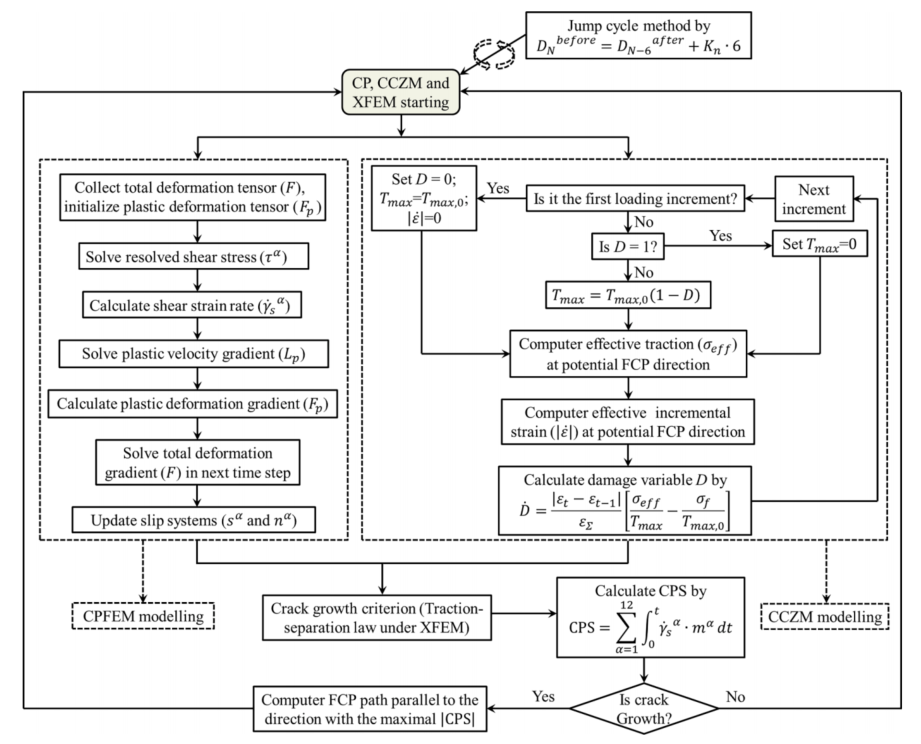
图:耦合模型集成了CP、CCZM、XFEM和循环跳跃技术的流程图。

图:模拟结果显示 FCP 在多晶体中的路径
文二:

不同尺寸煤试样中心裂纹圆盘的力学和断裂特性的实验研究
摘要:
裂缝在小范围内的传播会导致动态灾害,如煤层中大规模裂缝引起的岩爆。为了深入了解深部煤层断裂灾害的机理,本研究以不同尺寸的中心裂纹圆盘(CCCD)为特征,研究了煤样裂纹扩展的微观过程和尺寸效应。我们对不同尺寸的煤样进行了巴西劈裂试验,并采用声发射(AE)和数字图像相关(DIC)技术定量描述了裂纹的扩展过程。此外,还比较了不同直径的煤试样在拉伸破坏过程中不同断裂参数的尺寸效应特征。结果表明,随着试件尺寸的增加,准脆性破坏特征变得明显,抗拉强度逐渐降低并趋于稳定,而断裂韧性和断裂过程区长度逐渐增加并趋于稳定。煤试样中的宏观裂纹通常从试样的中心沿着预裂纹延伸到两端。大的能量事件主要集中在预裂纹的下端。随着煤样尺寸的增加,AE事件的数量减少,而大能量事件的比例逐渐增加,临界裂纹张开量随着尺寸的增加呈线性增加。通过对煤样进行断裂尺寸效应实验,我们将相关的力学参数从实验室规模的试验扩展到现场工程规模。这为基于断裂力学的原位煤大规模断裂过程分析提供了基本参数。

图:实验中使用的不同尺寸的煤试样

图:测试系统图

图:峰值拉伸应力和峰值载荷随煤样直径的变化。

图:煤样峰值载荷时刻声发射事件的空间分布。
文三:

基于真三轴分离-霍普金森压杆试验的煤岩冲击动力学行为及破坏特征研究
摘要:
充分了解煤样在真三轴条件下的动力力学特性,对防治深部煤岩动力灾害具有重要意义。研究结果表明,透射振幅随r1的增大而减小,随冲击速度的增大而增大。在真三轴条件下,煤的峰值应力和吸收能随着r1的增加而减小。在单轴和真三轴条件下,煤的峰值应力和吸收能随着冲击速度的增加而增加,并且在真三轴情况下的应力变化对动载荷的作用更敏感。与单轴冲击相比,煤样在真三轴条件下的损伤程度较低。破碎块体的分形维数随着r1和动载荷的增加而线性增加,表明破碎程度加剧。该研究有效揭示了煤在不等静载和动载作用下的破坏机理。
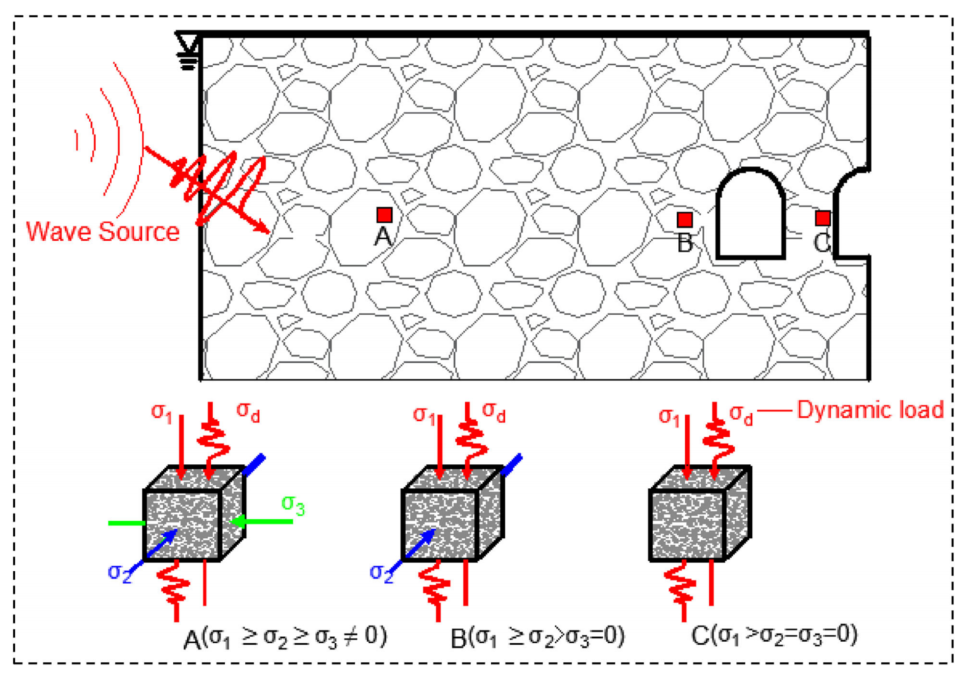
图:煤岩应力演化过程

图:煤样。

图:真三轴实验系统。

图:(a)实验设备的照片。(b)煤样装载路径
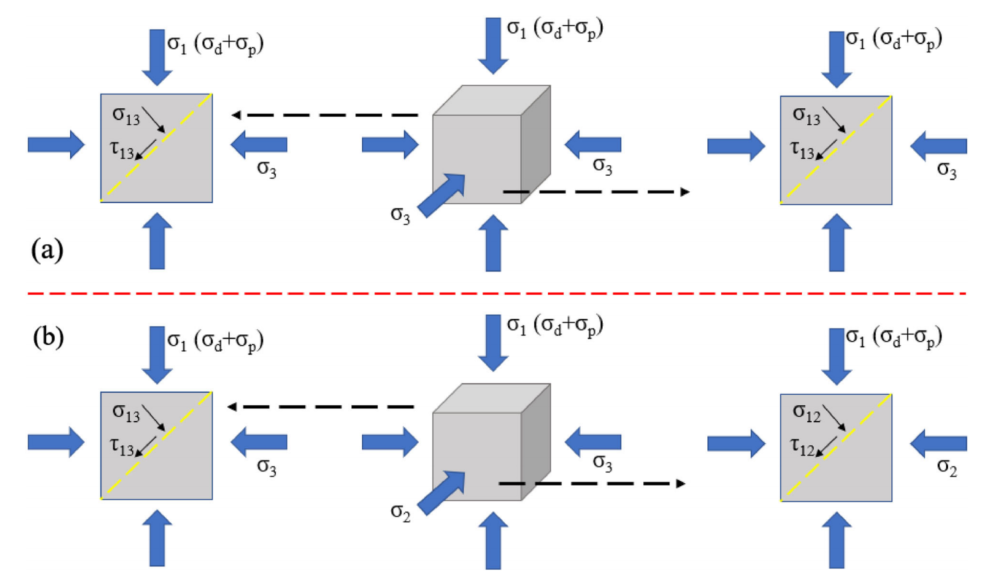
图:煤样应力状态
文四:

用于匹配脆性岩石单轴抗压强度与抗拉强度比值的改进颗粒接触模型
摘要:
商业离散元法(DEM)软件EDEM中的Hertz Mindlin with bonding(HMB)接触模型被广泛用于模拟和分析岩石的力学行为。然而,它无法与在玄武岩等脆性岩石中观察到的单轴抗压强度(UCS)与抗拉强度(TS)的高比率相匹配。在本研究中,通过充分考虑力矩对应力的贡献以及法向应力对剪切强度的影响,建立了一个改进的HMB接触模型。同时,提出了一种DEM参数反演方法,实现了对各种微观参数的快速准确标定。结果表明,修正后的HMB接触模型中的力矩贡献因子和最大抗拉强度是影响UCS/TS比值的两个关键参数。具体来说,弯矩贡献因子主要影响UCS,同时也共同影响TS和最大抗拉强度。改进的HMB接触模型成功地实现了与测试值一致的高UCS/TS比,并表现出显著的压力依赖性。该模型适用于精确模拟脆性岩石的力学行为。

图:应力-应变和应力-位移曲线:a单轴压缩试验,b巴西劈裂试验,c三轴压缩试验
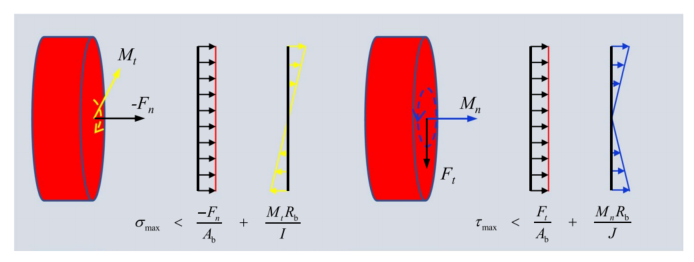
图:键的断裂条件

图:DEM参数反演方法
文五:

一种新的粗糙岩石剪切破裂非线性流动理论模型
摘要:
剪切变形显著影响岩石裂隙中流体流动的非线性。为了使用Izbash方程来估计这种非线性流动,有必要确定Izbassh系数。然而,它们的参数表达式很少被提及,尤其是当涉及剪切流过程时。本研究通过结合Darcy–Weisbach方程和摩擦因子,提出了一种改进的基于Izbash方程的模型。所提出的模型考虑了两种渐近情况。在低Re区域,流体流动区域由粘性效应主导,并且所提出的模型可以近似于三次定律。当Re达到某一阈值(Res)时,流体流动转变为完全湍流状态,其中惯性力主导流体行为。因此,所提出的模型等效于Forchheimer方程的二次项。在法向应力为0.5~3MPa的5个粗糙断裂面上进行的实验结果验证了该模型的正确性。实验曲线和分析曲线之间的良好相关性表明,所提出的具有强大理论基础的模型产生了良好的预测,归一化目标函数(NOF)和平均误差(σave)分别在0.18%和15%以内。

图:基于数据的样品S1和S2的Ta/To和Re与不同us的关系

图:剪切过程中Rec的变化




