增材制造最新研究:拓扑优化(topology optimization)和多尺度研究
文一:

用于增材制造的具有外壳层和界面层的多尺度拓扑优化
摘要:
本文提出了一种多尺度拓扑优化方法,用于同时具有壳体和晶格-晶格界面层的晶格结构设计,以增强结构的美观性、机械性和可制造性。为了提高鲁棒性,提出了一种多步算法。采用变厚度薄板(VTS)方法和基于投影的正则化机制来实现有限数量晶格微观结构的自由材料优化。然后,根据材料密度分布,采用一系列连续的滤波和投影操作来识别晶格-晶格界面层。密度相近的元素被分组成簇,对于每个簇内的元素,假设它们具有相同的周期性晶格微观结构。在第二步中,基于所获得的离散材料分布,使用基于密度的多尺度拓扑优化方法同时优化具有固体壳层的宏观结构和多个具有代表性的晶格微观结构。通过对几个基准数值例子的研究,验证了该方法的有效性。最后,进行了增材制造实验,以验证通过包括晶格-晶格界面层来增强刚度。

图:多孔复合材料的多尺度拓扑优化程序。

图:左边是不同步骤的密度场分布示意图。右图显示了相应密度场的1D物理密度函数。

图:设计域组合的概念说明:设计域(a)由一个固体界面层(b)和三个多孔填充物区域(c)组成。
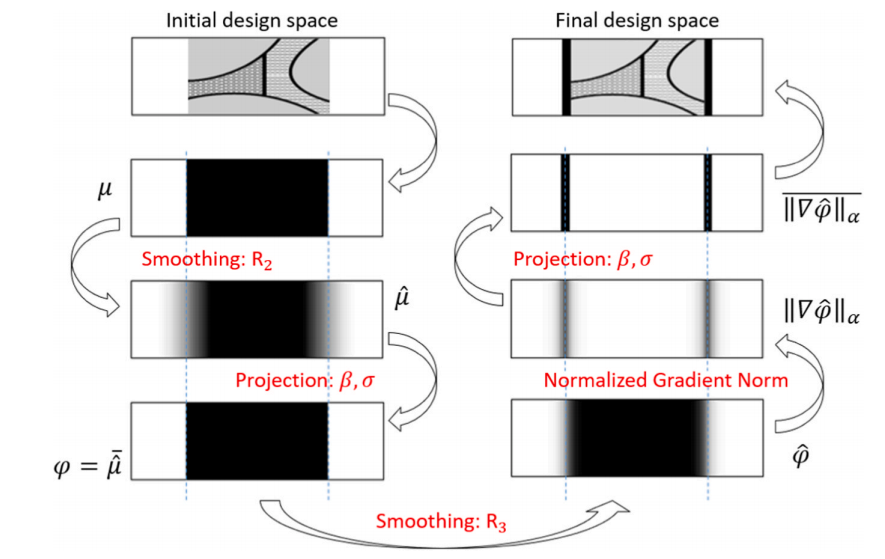
图:基本设计域与壳层分离的 DSP 方法。

图:三种材料微观结构的优化结果。

图:不同界面层和壳层厚度的优化结果。
文二:

多尺度多材料通道冷却蜂窝结构热力性能拓扑优化
摘要:
本文提出了一种并行的多尺度和多材料拓扑优化方法,用于设计包含冷却通道的蜂窝结构,以实现有效的隔热和承载能力。该结构由冷却通道、空隙和填充有隔热材料的金属晶格组成。在宏观设计尺度上考虑了具有设计相关热对流的热流体和机械力耦合模型,而在子尺度上采用基于数值均匀化和代理模型的方法来表征预定义准周期结构模式的有效热弹性特性。此外,还采用了基于惩罚多孔各向异性材料(PAMP)的多材料插值方案进行拓扑优化。该方法可用于轻型承载结构的多尺度拓扑设计,其中隔热和散热是除力学性能外的关键性能指标。由于多尺度复合材料配置具有更大的设计自由度,因此在类似的计算成本下,与单尺度基于固体的对应物相比,优化设计表现出更好的热力学性能。给出了几个设计实例和验证结果,证明了该方法的适用性。

图:多尺度通道冷却蜂窝结构:每一层(虚线)都包含由金属和隔热材料组成的次级复合晶格。

图:周期性复合晶格结构的均匀化。

图:由金属框架和隔热填充物组成的底层结构的单元。

图:复合晶格单元的可设计结构拓扑。

图:参数化复合格子有效性质的替代模型。

图:复合晶格分布。
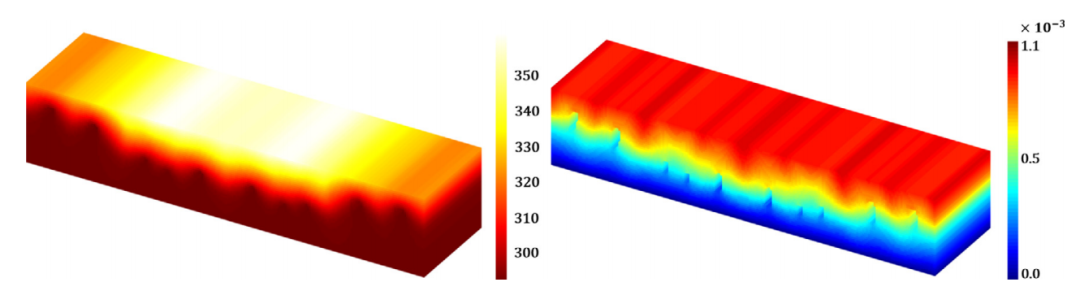
图:优化结构的温度(左)和位移(右)。

图:通过单尺度方法优化的结构和相应的温度场。

图:热保护室的几何形状和边界条件。
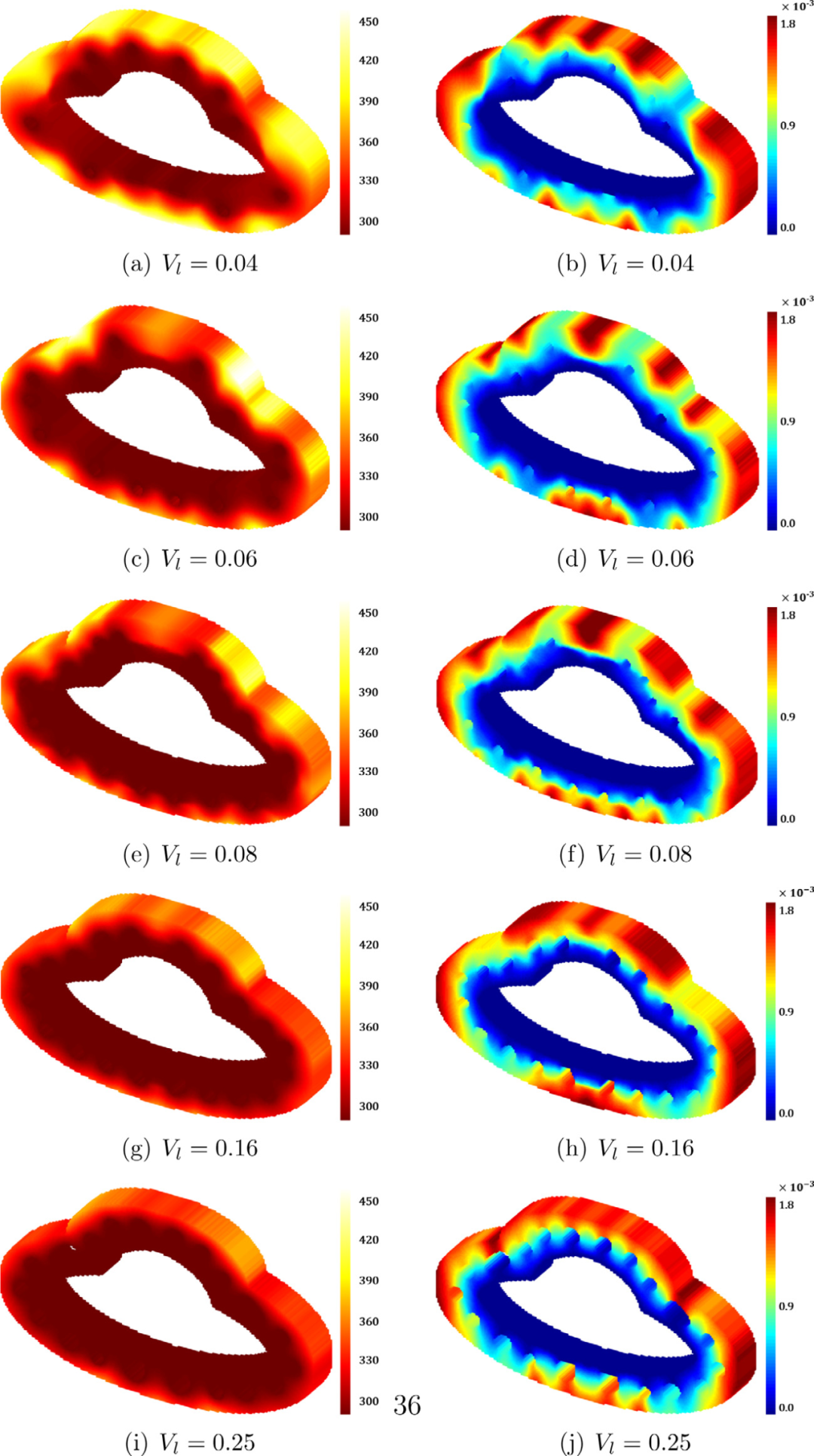
图:不同冷却液体积下优化结构的温度场(左)和位移场(右)
文三:

多尺度并行拓扑优化问题的一种有效解耦灵敏度分析方法
摘要:
并行拓扑优化问题的传统耦合灵敏度分析方法对于微型设计变量来说计算成本很高。因此,本文提出了一种基于链微分规则的并行拓扑优化解耦灵敏度分析方法。进行了两个数值研究,以证明解耦灵敏度分析方法对单个或多个多孔材料并发拓扑优化问题的有效性。从结果可以得出结论,解耦方法在计算上比耦合方法有效得多,但它们在数学上是等效的。解耦方法的突出优点有两个方面:(1)灵敏度分析对微尺度设计变量的计算效率;以及(2)适用于单个或多个多孔材料以及复合微观结构和多相材料的并发拓扑优化问题。

图:单孔材料两尺度并行拓扑优化框架

图:具有多种多孔材料的两尺度并行拓扑优化框架

图:单一多孔材料耦合法和解耦法灵敏度的比较
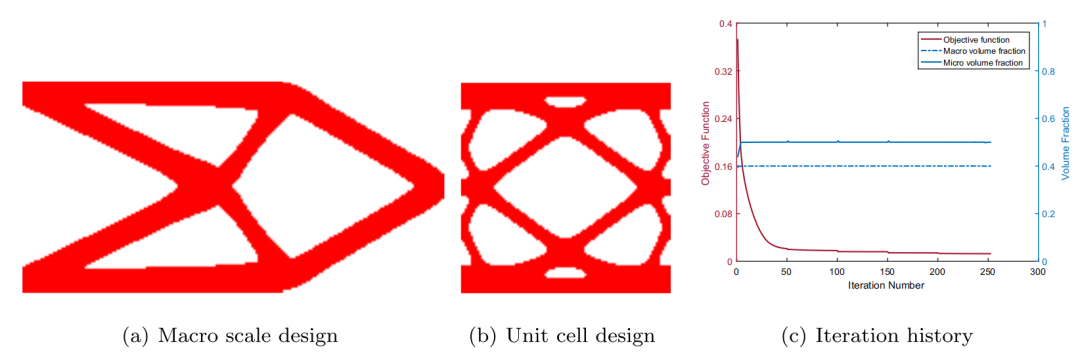
图:单一多孔材料并发拓扑优化结果

图:单一多孔材料的耦合方法和解耦方法计算时间的比较

图:三种多孔材料的并行拓扑优化结果
文四:

基于 Kriging 元模型的非均匀微结构单元结构并行拓扑优化
摘要:
本文提出了一种新的多尺度并行拓扑优化方法,用于在空间中具有连续变化微观结构的单元结构,以在可承受的计算成本下获得优越的结构性能。在微观尺度上,通过将数值均匀化方法纳入参数水平集方法(PLSM),对多个原型微观结构进行拓扑优化,以表示宏观结构中的所有微观结构,该方法的连通性由运动学连接约束方法保证。开发了一种形状插值技术来映射这些优化的原型微观结构,并生成一系列不均匀的微观结构,这些微观结构被视为样本点,用于构建克里格元模型。然后使用所建立的克里格元模型来预测宏观结构中所有非均匀微观结构的有效性质。在宏观尺度上,利用所有非均匀微观结构的预测有效特性,采用变厚度薄板(VTS)方法生成整体自由材料分布图。在形状插值技术的帮助下,宏观结构中的所有非均匀微观结构由于其界面处的拓扑特征相似而相互连接良好。使用所提出的方法,可以同时优化宏观结构拓扑以及空间变化的非均匀微观结构的位置和配置,以确保足够大的多尺度设计空间。通过算例验证了该方法的有效性和优越性。

图:图解说明级别集函数的形状映射技术的示例

图:演示形状映射技术和克里格元模型的测试示例

图:具有空间变化的不均匀微观结构的宏观结构示意图

图:提出方法的数值实施流程图
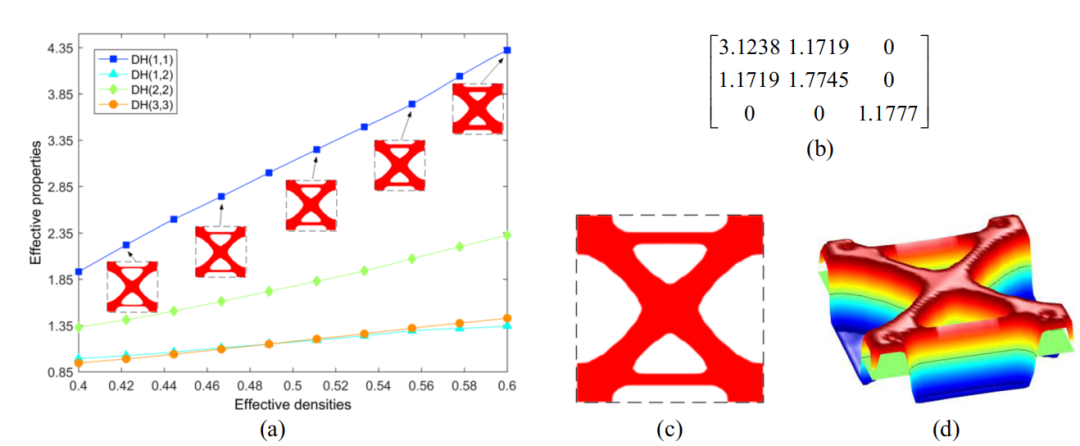
图:a. 映射的非均匀微观结构的有效性质变化与其有效密度及其配置的图表。b有效密度为0.5的优化原型微观结构的有效性质、c构型和d水平集函数

图:目标函数和全局体积约束的迭代历史

图:体积分数为30%的多尺度并行设计。合规性为702.0868
文五:

基于Matlab的多尺度复合材料结构并行拓扑优化
摘要:
本文提出了紧凑高效的Matlab代码,用于多尺度复合材料结构的并行拓扑优化,不仅在二维情况下,而且在考虑三维情况下。采用改进的SIMP方法(Sigmund 2007)来实现并行拓扑设计,并采用基于能量的均匀化方法(EBHM)来评估微观结构的宏观有效性能。本文中的二维和三维Matlab代码分别使用88行二维SIMP代码(Struct MultiscOptim 43(1):2011年1月16日)和169行三维拓扑优化代码(Strust MultiscOptimize 50(6):1175–11962014)开发。本文主要致力于以下四个方面:(1)蜂窝复合材料结构拓扑优化的代码体系结构(ConTop2D.m和ConTop3D.m),(2)计算三维等参单元刚度矩阵的代码(elementMatVec3D.m,以及(4)在两个尺度上计算目标函数相对于设计变量的灵敏度的代码。测试了几个数值示例,以证明附录中所附的Matlab代码的有效性,也为新加入者使用拓扑优化设计蜂窝复合材料提供了一个切入点。
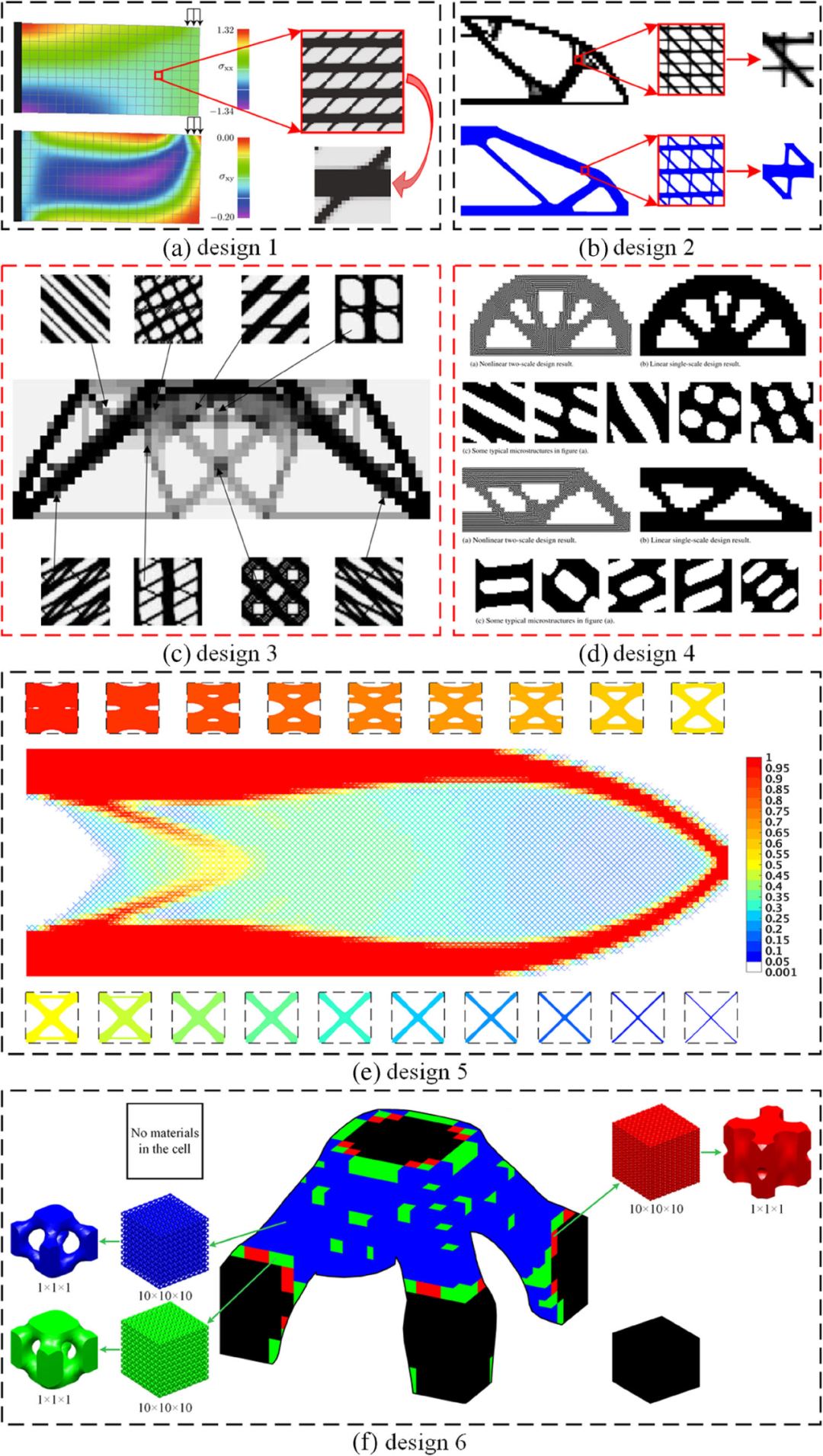
图:几种并行多尺度设计。

图:二维双比例结构。a宏观结构。b微观结构

图:多尺度复合材料结构的并行拓扑优化
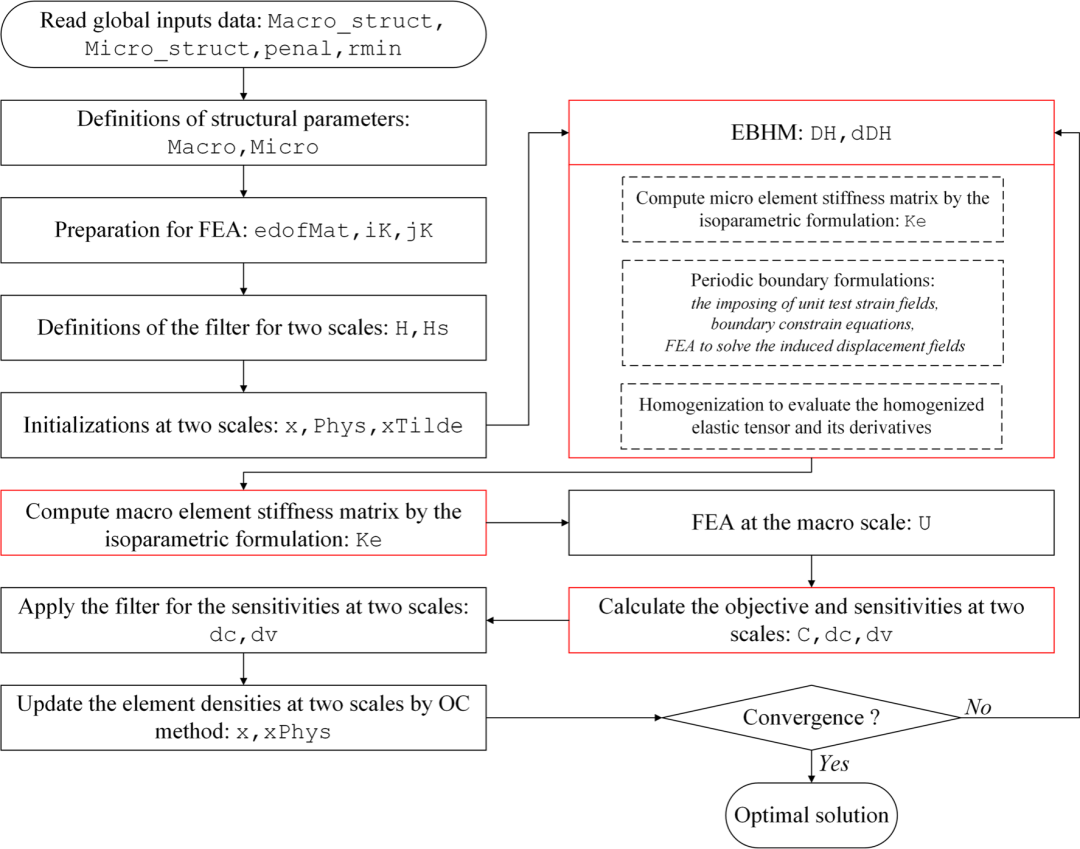
图:用于并行拓扑优化的2D和3D代码的流程图。

图:微观结构中不同类型的节点。a位于顶点的节点。b位于边缘的节点。c位于表面的节点。d位于内部的节点。

图:迭代历史。a目标和宏观体积分数。b微体积分数

图:柔顺机构的并行拓扑设计。a. 单尺度。b. 均匀的微观结构。c. 具有12个微观结构的并行设计




