湍流模拟|10 再附修正
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家
- 平台推荐
- 内容稀缺
NASA 驼峰流[46]–[48](图58)的主要关注点是评估湍流模型预测从光滑物体(由逆压力梯度引起)分离,以及随后的再附着和边界层恢复情况。自其被引入以来,这个案例已被证明对所有已知RANS模型都是一个挑战。

湍流模型往往低估了分离剪切层中的湍流剪应力和湍流动能,因此预测的分离泡过长。这是所有RANS模型共同存在的问题,也是这类模型系列的主要未解决缺陷之一。值得注意的是,在分离由几何形状决定的情况下(如在后向台阶流场中,参见图1)不会观察到这种现象。这两种情况之间的差异似乎在于驼峰流动中的分离线可能存在潜在的不稳定性,这可能导致小尺度的涡脱落。这种影响原则上超出了RANS模型的研究范畴,因为其构成了非定常流而非湍流。当然,人们渴望利用现有的RANS模型模拟此类效应,否则就需要使用成本更高的尺度解析模拟。为此,人们已经提出了各种高度临时性的RANS模型改进方法,这些方法并未被广泛使用,通常情况下不应激活。然而,在某些应用中,这些方法展现出一定的改进效果,因此这里将讨论其中的一种方法。本文所提出的模型已在CFX中实现。该方法公式也被Rumsey在NASA技术备忘录[49]中采用,但使用的模型系数不同。


通过调整GEKO模型可以改善对再附着点的预测效果。图61展示了降低 系数对再附着点预测的影响。当 取值为1.00时(如图62所示),速度和雷诺应力的预测得到了改善,但代价是分离起始点的预测会被延迟。然而值得注意的是,在分离区域中的雷诺正应力 仍然被低估,并且几乎与
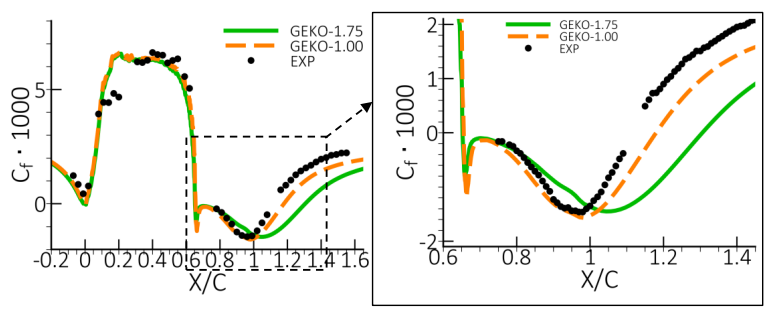


再次强调,将
注:系列翻译自《Best Practice: RANS Turbulence Modelingin Ansys CFD》,作者F.R. Mentor,2022
”
(待续)




