算例丨HyperMesh联合LS-DYNA的汽车车门刚度与强度仿真分析流程

1 引言
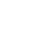
车门是车身的重要组成部分,当车门刚度不足,容易造成车门开启困难、密封不好、漏风渗雨等问题,从而导致车门产生噪声和振动,大大降低乘坐舒适性,使得人员体验度下降,降低产品质量。因此,对车门进行下沉刚度分析很有必要,有限元分析是验证车门刚度的重要手段。
Hyperworks是汽车行业广泛应用的前后处理软件,其与多个求解器软件有很好的接口,比如Abaqus、LS-DYNA、Nastran、Ansys、Optistruct等,汽车行业一般用Hypermesh为其他求解器搭建有限元模型。LS-DYNA能够模拟真实世界的各种复杂问题,非常适合求解三维非线性结构的碰撞、金属成型等非线性动力学冲击问题,以Lagrange算法为主,兼有ALE和Euler算法,以显式算法为主并有隐式算法,是通用的结构非线性有限元分析程序。
本文利用Hyperworks软件对车门建立有限元模型,在Hypermesh中搭建LS-DYNA求解器的CAE模型,在LS-DYNA中用隐式算法进行求解,对设计车前车门进行下沉分析,以了解其抵抗垂向变形的能力,为结构设计提供参考依据。

2 某轿车前车门有限元模型
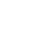
针对某新型电动乘用车前车门下沉分析所用有限元模型,如图1所示。
有限元建模过程中,对模型进行几何清理和几何简化,对薄板进行抽中面处理,铰链保留实体,划分实体单元,截取白车身部分,用铰链与其连接,白车身和车门部分用点焊和二氧化碳保护焊连接,前挡风玻璃和前车门玻璃用胶粘连接。网格采用四边形、三角形和四面体单元,用8mm大小划分网格,三角形单元总数不超过5%,该有限元模型重量为25.6Kg,节点数量为264882,单元数量为255874。

3 前车门材料属性



4 边界条件

约束车身断面处的平动自由度;约束车身与底盘连接处的全部自由度;约束锁扣处的侧向平动自由度;考虑铰链与侧围外板和车门内板之间的接触作用;考虑侧围外板和车门内板与各自加强板之间的接触作用。


5 计算结果与分析

车门在自重工况下的位移云图如图3 所示,从图中可以看出车门在自重下的最大变形量为1.78mm,发生在车门右上角。车门在自重工况下两铰链处的应力云图如图4 所示,从图中可以看出下铰链处所受应力较大,最大应力值为255MPa。


车门在保持车门自身重力,在门锁处施加沿Z 轴负向的载荷1000N 工况下的位移云图如图5 所示,从图中可以看出车门在自重下的最大变形量为9.83mm,发生在车门右上角。车门在保持车门自身重力,在门锁处施加沿Z 轴负向的载荷1000N 工况下两铰链处的应力云图如图6 所示,从图中可以看出上下铰链处所受应力相差不大,最大应力值为386MPa。

图5 门锁处施加沿Z 轴负向的载荷



车门在保持车门自身重力,移除外载工况下的位移云图如图7 所示,从图中可以看出车门在自重下的最大变形量为3.07mm,发生在车门右上角。车门在保持车门自身重力,移除外载工况下两铰链处的应力云图如图8所示,从图中可以看出下铰链处所受应力较大,最大应力值为278MPa。


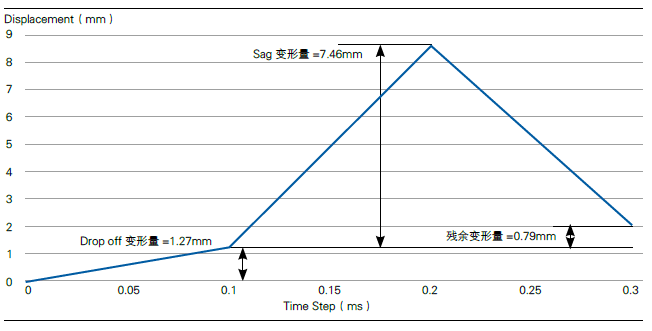
表2 门锁处垂向位移


6 结论








