用于经导管二尖瓣置换术的支架有限元评估
摘 要:
目的:提出一种经导管二尖瓣置换术支架设计,评估支架与瓣叶植入后在体内相互作用产生的变形情况并分析其力学行为。方法:应用有限元方法,建立支架瓣叶组合模型,在瓣叶上施加压强载荷模拟其在人体内闭合的过程,分析其变形情况和应力应变结果以及受此影响的疲劳寿命。结果:本支架受瓣叶牵拉产生的最大顶端位移为0.24 mm,周期性应变的疲劳寿命约为2.05×108次。结论:变形程度可接受但不可忽视,瓣叶的周期性牵拉对支架的影响可使其在人体内正常工作5~9年。
关键词:经导管二尖瓣置换术;二尖瓣支架;有限元分析;
前言
二尖瓣反流是全球范围内最常见的心脏疾病之一,根据一项针对35岁以上人群的调查研究显示,我国自然人群的二尖瓣反流检出率为18.4%,其中中重度二尖瓣反流检出率为1.2%[1,2]。常见的治疗手段包括药物治疗、外科手术治疗和介入手术治疗3种[3]。对于二尖瓣反流较重的患者,单纯药物治疗效果不佳,需要采取手术治疗。而传统的开胸外科手术对于老年患者或合并有其他疾病或手术并发症的患者有较高的危险,而这两种情况却在重度二尖瓣反流的患者群体中经常发生。近年来随着技术的成熟,介入手术逐渐成为替代传统开胸手术的新治疗选择[4]。介入手术主要有两种方法:经导管二尖瓣置换术(Transcatheter Mitral Valve Replacement,TMVR)和经导管二尖瓣修复术。其中,TMVR往往用于更重程度的二尖瓣反流患者的治疗[5,6,7]。2012年6月12日丹麦哥本哈根大学Rigshospitalet附属医院完成了世界上首例人体TMVR,此后二尖瓣病变的治疗手段迎来了新的选择[8]。目前多种TMVR瓣膜已进入临床试验阶段并初步取得了良好的随访结果[9],然而TMVR目前仍面临诸多的问题和挑战,包括二尖瓣瓣环质地松软难以固定、二尖瓣环随心动周期收缩变化带来的瓣叶和支架耐久性问题等[10]。支架的耐久性不足可能出现支架失效、移位、漏斗状变形等情况,甚至对病人造成生命威胁。
二尖瓣支架植入后需要长期承受血流压力和冲击力等不同形式负荷,在有限元模拟中也需要考虑多种相互作用。冒鹏志等[11]研究了二尖瓣支架受心脏搏动的影响,Tanimura等[12]研究了支架与动脉之间的接触作用,Kumar等[13]在支架上施加均匀压力载荷以研究瓣叶负荷。总的来说,在过去的研究中,前人往往将支架、瓣叶两者分开研究[14,15],或者在组合模型中将支架视为刚体,不讨论其变形。然而实际中的瓣叶由于受跨瓣压差作用产生周期性的开闭,会对支架产生一定的牵拉变形,支架在体内变形可能会导致置换的二尖瓣无法紧密地关闭或开启,从而影响心脏的正常功能。这可能导致血液回流和心脏扩大,甚至增加心脏负荷,导致心力衰竭等严重后果,因此建立一个考虑其相互影响的支架-瓣叶组装模型将对后续的研究有重要意义。本文提出了一种用于TMVR的二尖瓣设计模型,该设计由镍钛合金支架和生物材料瓣膜组成。瓣叶采取三瓣式设计,有良好的闭合效果。支架内部缝合生物瓣叶,经导管压缩植入人体,与成形环缝合固定。
本文的研究目的是:(1)建立支架-瓣叶组装模型,评估其可行性和安全性;(2)计算其在正常心动周期中受跨瓣压差变形的结果,分析其应力、应变等分布情况。这一模型可以帮助支架设计者直观感受支架受瓣叶周期性牵拉带来的影响,辅助其优化支架的结构设计,避免产品在植入人体后产生瓣周漏等问题。
1 材料与方法
1.1 支架设计与材料选择
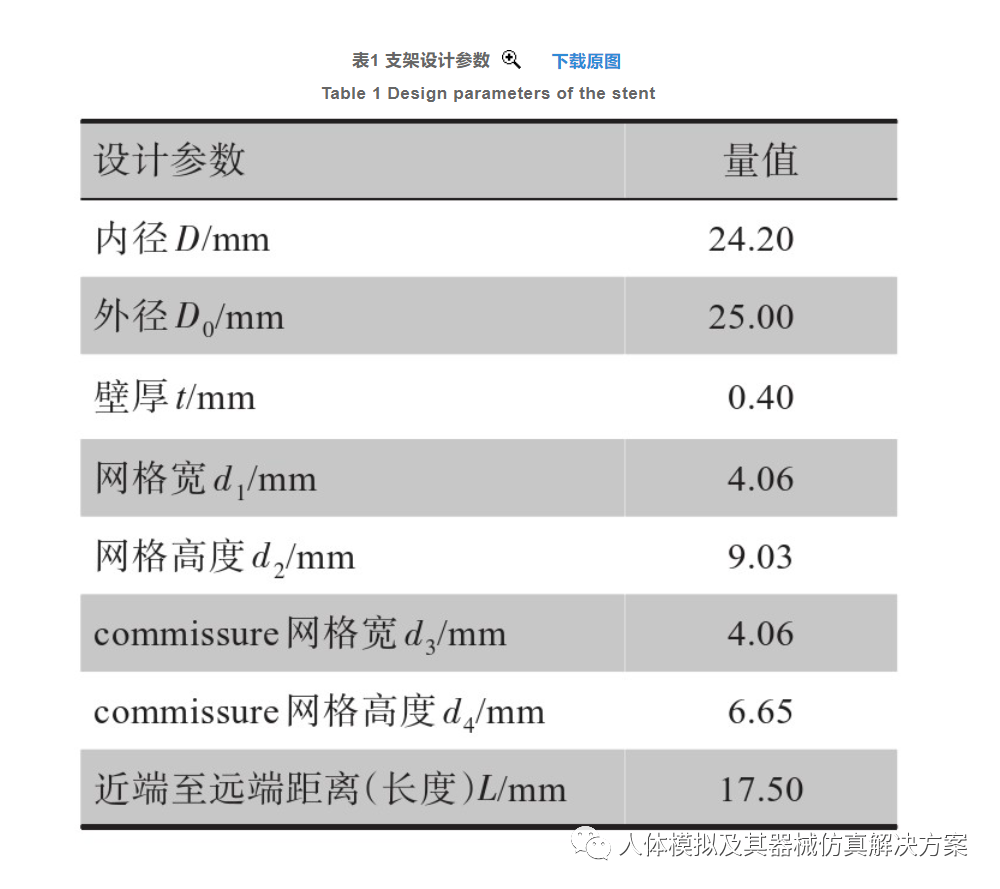
支架的设计基于二尖瓣环组织的几何形状,设计满足支架压缩进入导管的尺寸要求,同时保证其应力分布相对均匀,对应力较大的区域进行加厚设计。支架底部与3片人造瓣叶的几何轮廓线相匹配,便于定位与缝合,同时和底部支架、成型环结构相对应,具体尺寸如表1所示。通过Solidworks软件绘制支架、瓣叶模型图,导入到Hypermesh中进行有限元网格划分,之后使用Abaqus进行模拟计算以及完成后处理工作。
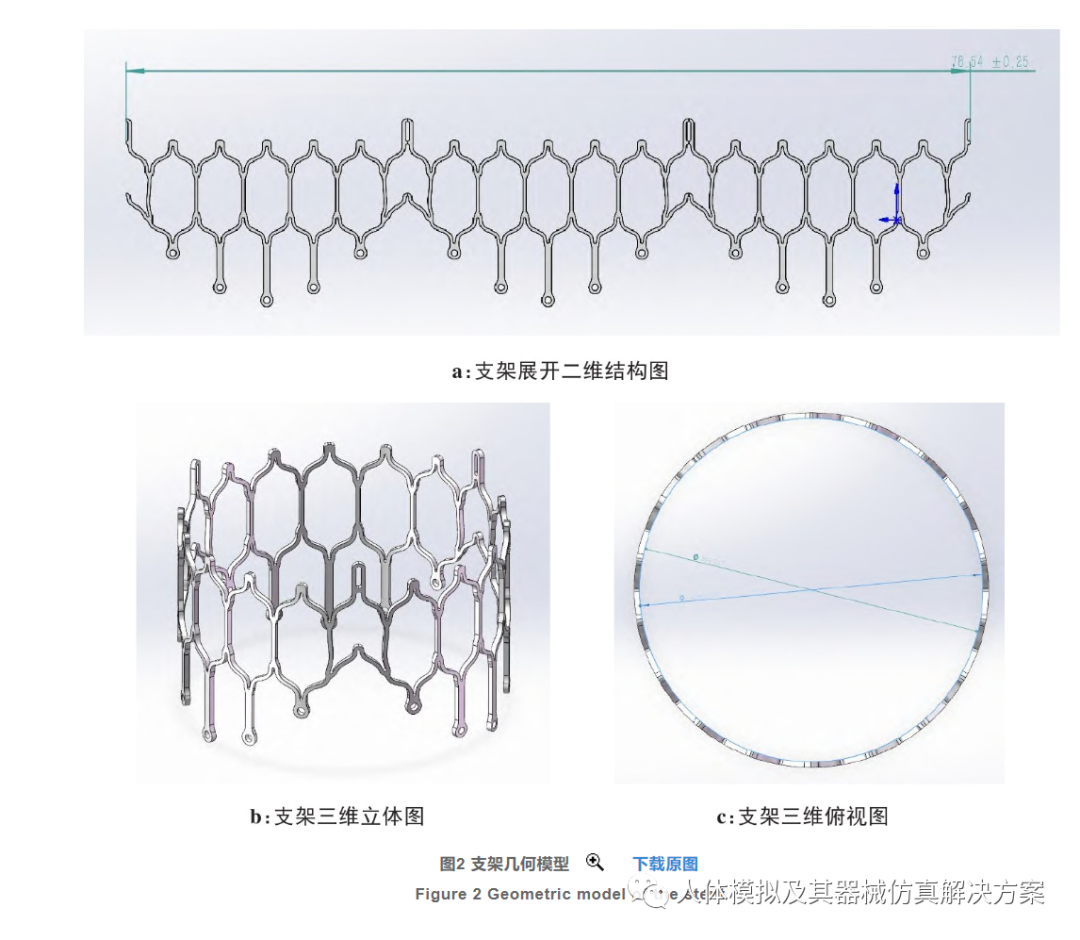
通过CAD建模软件Abaqus建立二尖瓣支架的几何模型,首先绘制1/6支架的草图,如图1所示。这一设计的主体结构可以满足TMVR对支架压缩扩张能力的要求,下方高低不平的尾端设计方便与底部起到固定作用的底座相配合。然后拉伸0.4 mm厚的实体,经过一次180°的镜像和两次120°的阵列组合,最终弯曲形成外径25 mm的支架实体(图2)。

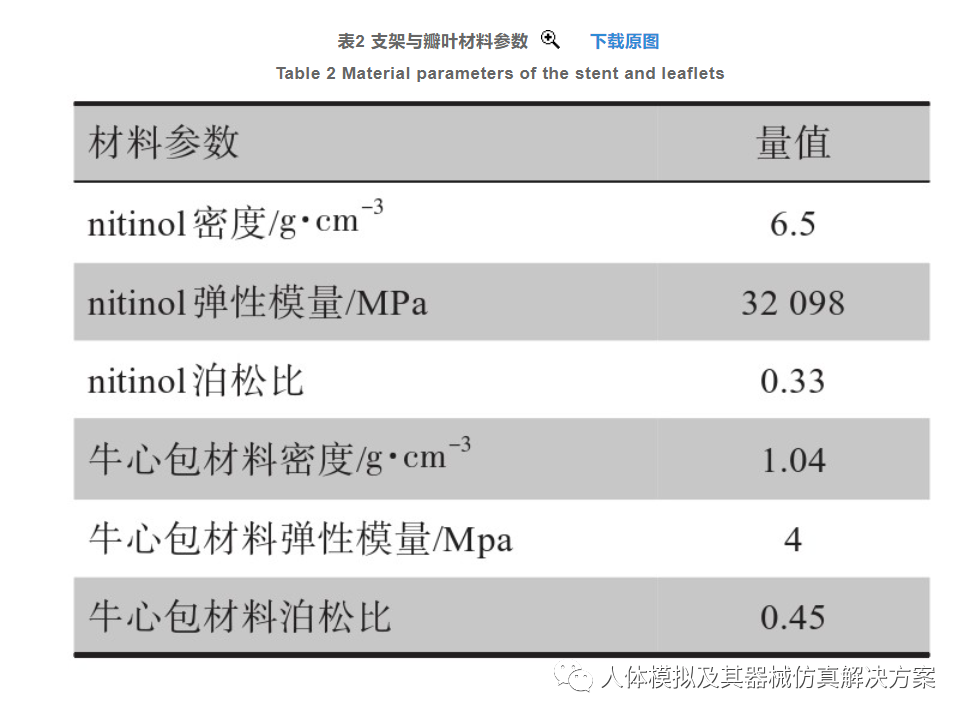
支架材料因为其应用情景的特殊性,需要满足许多苛刻的条件。目前大多数的医用血管支架可选择的材料有医用不锈钢、金属钽、镍钛合金以及可降解的高分子聚合物等。由于本支架旨在用于TMVR,因此需要有优秀的超弹性和形状记忆能力[16]。因此本设计中选用nitinol合金材料,具有良好的形状记忆能力和生物相容性,瓣叶采用牛心包材料,其材料参数如表2所示。对于nitinol材料,在Abaqus中还需设置其超弹性参数(Super Elasticity),如表3所示。
1.2 有限元分析
支架与瓣叶的组装模型如图3所示,瓣叶在支架内部与其共轴,底部接触部分在实际手术中需缝合在一起,因此在Abaqus软件中设置面与面接触,接触类型为罚函数接触,不考虑接触面的摩擦。瓣叶厚度0.2 mm,底边长度为33.93 mm,与支架底部轮廓线一致,上边长度为22.81 mm,自由展开,在闭合时三瓣叶可以完全封闭。
在本模型中,边界条件的设置主要考虑以下两点:(1)在实际应用中,支架下方有一硬质底座起到固定、支撑支架的作用,因此在支架底部15个圆环处设置固定约束,三个维度的位移:U1=0、U2=0、U3=0。(2)瓣叶底部与支架底部紧紧缝合,因此将瓣叶下边缘设置为:U1=0、U2=0、U3=0,使其位置固定但保留偏转自由。

载荷的设置需要与实际瓣叶受到的压力情况相吻合,瓣叶同时承受心房和心室两侧的压力,心房、心室压在一个心动周期内的压力值数据如图4a所示[17]。图4b是由图4a计算得到的跨瓣压差曲线,由图可知,瓣叶闭合阶段瓣膜受到的房、室压差近似为:在初始的0.1 s内线性增长,由0增长到16 kPa;在随后的0.1 s内,保持16 kPa恒定。
本模型由于瓣叶在短时间内产生较大变形,因此需要选择动力学分析步,并为其设置质量缩放来加快计算速度。根据图4b所示曲线,时间长度设置为0.2 s,与实际相符。本模型由于本身计算时间成本较高,需要设置质量缩放以加快计算速度,在经过调试后,选择引入值为20的质量缩放系数,此时计算结果显示动能约为系统总内能的0.14%,远低于衡量标准的5%,因此可认为这一质量缩放系数是合理的,即在提高计算速度的同时并未影响模型准确性。
2 结果
2.1 支架结果云图
如图5所示,支架-瓣叶组装模型中支架的应力最大值为133 MPa,其对应的应变值最大为0.175%。支架位移云图中位移最高的点位于支架顶端,大小为0.235 3 mm,达到支架厚度(0.4 mm)的一半以上,这说明瓣叶周期性开闭对支架的变形影响不可忽视。


2.2 支架应力应变
使用Origin 2019对应力数据进行分析,以10 MPa为一个区间,统计频数,计算相对频率,如图6所示。应力最大值是133 MPa,占比最多(70.0%)的应力节点在0~10 MPa区间,绝大部分应力节点(96.3%)在30 MPa以内,仅有极少数应力节点(1.35%)在40 MPa以上。以0.01%为一个区间统计应变频率分布,最大应变值为0.175%,占比最多(43.8%)的应变在0~0.01%的区间,大部分节点(75.5%)的应变在0.03%以内,仅有极少数节点(1.15%)的应变值在0.1%以上,结果如图6所示。
二尖瓣支架设计必须符合相应的规范和要求,以确保安全和有效性。在生产过程中,支架的尺寸、形状、重量、结构和力学特性等都需要进行精确控制,如果一个直径25 mm的二尖瓣支架的顶端向内偏移0.23 mm,可能会对其性能产生一些影响。在血流动力学方面,支架的顶部偏移可能会增加血流动态的复杂性,导致更多的涡流、扰流和接触压力,增加血栓和栓塞的风险。在密封性方面,支架的偏移可能会影响二尖瓣的密封性,导致更多的反流和漏出。在使用寿命方面,支架的某个部位向内偏移可能会增加与其他器械或组织接触的机会,并产生额外的机械磨损,加速在手术后使用寿命中的疲劳循环。因此,即使是微小的二尖瓣支架顶部偏移也可能导致严重的并发症,这需要医生通过详细的评估确定其对患者的健康影响是否达到治疗或更正的程度。如果支架的偏移超过正常范围,则需要重新操作或更换支架来确保二尖瓣能够正常工作。
2.3 瓣叶结果云图
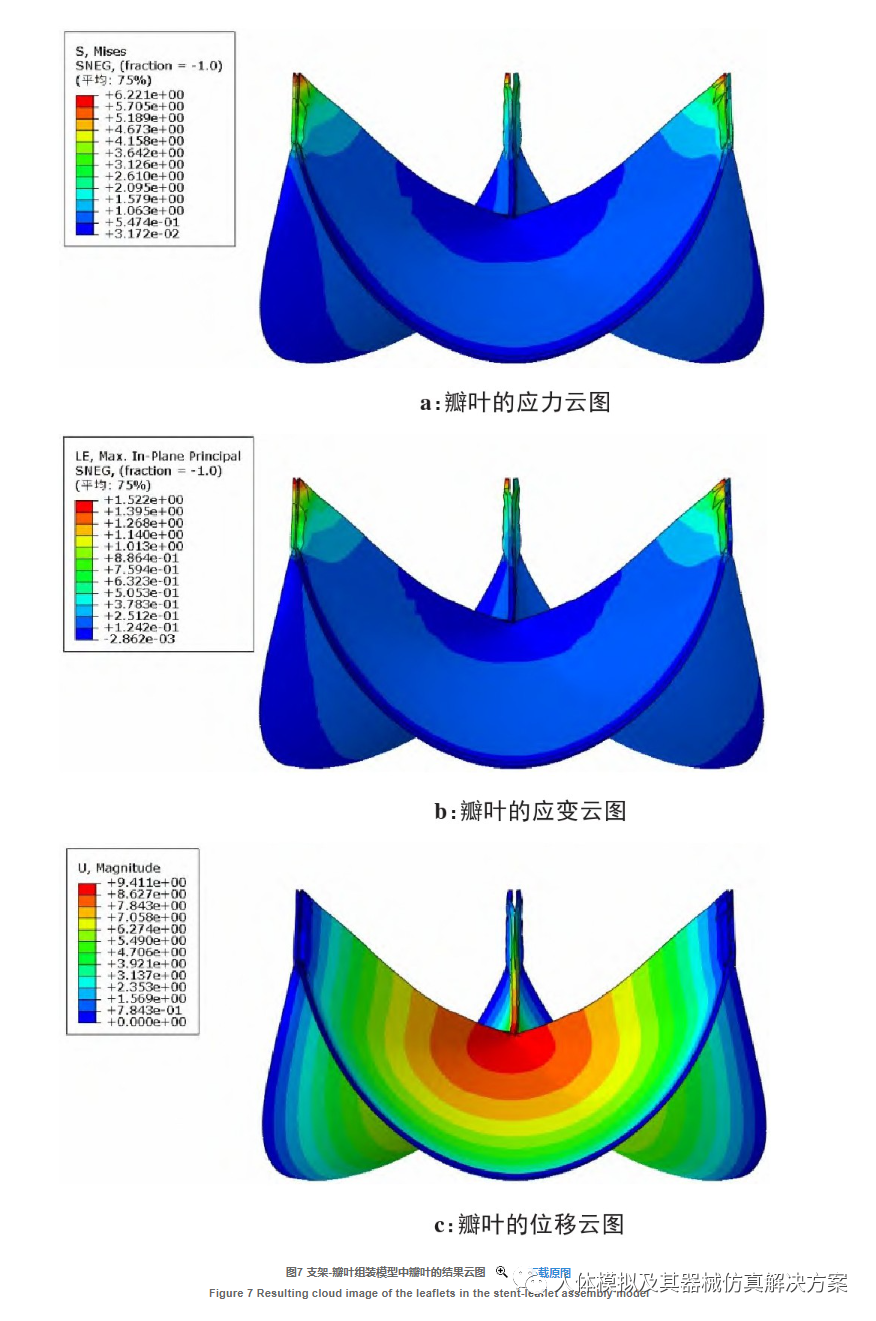
本模型同时考虑了支架和瓣叶两者在跨瓣压差作用下的变形情况,图7是支架-瓣叶组装模型中瓣叶的应力、应变和位移云图,其中最大应力为6.221 MPa,对应的最大应变为152.2%。王野峰等[18]的研究表明,牛心包组织经不同处理方法处理后,极限抗拉强度最少能达到11.66 MPa,因此本模型中瓣叶不会被损坏。


2.4 瓣叶应力应变
同样使用Origin 2019对瓣叶各节点的应力应变结果进行统计分析。以0.5 MPa为一个区间进行应力频率统计,相对频率最高(64.6%)的应力区间为0.5~1 MPa,大部分(93.5%)的节点应力值在1 MPa以内,仅有极少数(1.09%)的节点应力值在2 MPa以上。以10%为一个区间对应变进行频率统计,与应力对应的是,相对频率最高(68.8%)的应变区间是10%~20%,大部分(95.6%)节点的应变值在0~30%区间,极少数(1.93%)的节点应变值在40%以上,应变值最大的节点应变为152.2%,具体结果如图8所示。
由瓣叶的应力应变云图可以清楚看到,瓣叶上的应力由于其结构的对称性,呈对称分布,最大的应变、应力区域处在瓣叶与支架commissure部分接触的两个角区域。
3 讨论
在本文的研究中,提出了一种全新的支架-瓣叶组合模型,即充分考虑了瓣叶的周期性闭合过程对支架产生的牵拉作用。对于过去的研究,有些考虑支架与心肌组织的作用、支架与血流的作用、支架受心脏搏动影响,却忽视了瓣叶对支架的牵拉。但实际应用过程中,瓣叶牵拉使支架变形的情况客观存在,建立相应的有限元模型可以帮助支架设计者提前完善支架的几何结构,节省实验后修改设计所消耗的时间成本和经济成本。
3.1 疲劳寿命
材料力学疲劳寿命公式:

其中,K是材料的疲劳强度,Δσ是应力振幅,可以通过哈钦斯基-格林应变公式来计算:

其中,E为材料的杨氏模量,镍钛合金在37℃时的疲劳强度可以达到1 100 MPa左右,可以通过材料力学疲劳寿命公式来计算镍钛合金的疲劳寿命。材料的疲劳指数n通常由其S-N曲线给出。在没有更具体材料信息的情况下,n的值可以根据经验公式进行估算。一些研究表明,大多数金属在高周疲劳区(如在104级以上的循环寿命区域)的n值为0.1~0.6。对于镍钛合金,一些研究表明,在高周疲劳区,n值通常为0.3~0.4。因此本文选取n=0.3进行计算,将数值带入公式计算得N=2.05×108。
因此,在0.175%应变下,本文支架疲劳寿命约为2.05×108次。这个估算值仅考虑了材料的疲劳强度和弹性模量等基本性质,实际疲劳寿命还需要考虑支架结构的特性、应力分布、外界环境以及使用条件等。成年人的正常心率范围是60~100次/min。因此,一个成年人一年的平均心跳次数为2 500~4 000万次,因此该支架在仅考虑自然心动周期中瓣叶牵拉的作用下,可以正常工作5~9年。

3.2 后续工作
本文将血液对瓣叶的作用视为周期性均匀施加的跨瓣压差,后续的研究可以考虑血液、人造瓣叶、支架与心原生组织之间的耦合作用,模拟左心室涡流等使模型更加真实可靠。还可以在此模型的基础上研究不断发生周期性变形后的支架,在植入人体多长时间后产生反流等失效情况,以预测不得不再次进行介入治疗的时间。
4 结语
本文提出了一种用于TMVR的支架设计,并以此为例,提出了一种全新有限元仿真模型的建立方法,其特点在于充分考虑了支架在二尖瓣开闭过程中受其牵拉作用而产生的变形。这一变形会随着每一次心动周期而产生,在其长久的作用下将显著影响支架在体内的形态,进而会影响瓣叶的关闭状况,影响支架-瓣叶系统的正常工作。建立有限元模型对其进行研究可以为支架设计修正提供指导。有限元分析结果表明:(1)支架受到瓣叶的牵拉会产生一定的形变,大小约为支架厚度的一半,这一变形在长久积累下会对支架结构产生不可忽视的影响。(2)支架变形集中在接合处的支架单元,修改此处的几何结构可以降低牵拉应变的程度。(3)牵拉产生的周期性应变的疲劳寿命约为2.05×108次,可正常工作5~9年。本模型不仅可用于二尖瓣支架,也可为其他支架与瓣叶的相互作用研究提供参考。
参考文献:[1]陈一然,贺照明.用于经导管二尖瓣置换术的支架有限元评估[J].中国医学物理学杂志,2023,40(10):1302-1308.
免责说明:文章仅供交流学习,版权归原作者所有。如有涉及版权,请联系删除!




