湍流射流中示踪粒子的跟随性数值模拟分析
国内外学者从数学分析和数值计算的角度对示踪粒子的跟随性问题进行了大量的研究工作,发现:对于简单流场以及一些速度空间分布比较均匀而随时间剧烈脉动的复杂流场,密度与流体接近的、小粒径(小于10μm)的粒子对流动具有较好的跟随性。目前对于示踪粒子在速度分布非均匀的比较复杂的流场(如射流流场)中的跟随性的研究较少。
流场测量新方法研究及流场测量,单帧单曝光方法和单帧多曝光方法都采用示踪粒子的速度来表征射流流场速度,需要对其跟随性进行分析,尤其对于背光式示踪粒子三维速度测量方法,为实现颗粒的三维定位,该方法下示踪粒子的尺寸越大,越有利于图像识别与处理,而跟随性要求又希望其尺寸尽量小,对这种经典流动结构中的粒子跟随性进行研究,可以对示踪粒子的选取和实验数据的分析进行指导。
本文从数值模拟角度对实验条件下水射流流场中聚苯乙烯颗粒的跟随特性进行研究:
大涡模拟求解射流流场
首先,采用大涡模拟方法求解射流流场,并与实验结果进行对比,验证流场模型的可行性。
验证离散相模型的准确性
然后,定义了密度与水相同的5种不同粒径的虚拟颗粒,将其响应时间的理论分析结果与数值模拟结果进行对比,验证了离散相模型的准确性。
数值模拟及分析
最后,利用上述模型对11种不同粒径的聚苯乙烯颗粒进行数值模拟,并将其轨迹与质点轨迹进行对比分析,提出了聚苯乙烯颗粒粒径选取的推荐范围。
1
数值方法
在湍流流场中,起主导作用的是大尺寸的漩涡,大涡造成了湍流的混合与脉动,而小尺寸的漩涡主要引起湍流动量的扩散。大涡模拟(LES)方法的主要思想是通过滤波处理将大尺度的涡和小尺度的涡分离开。对大涡进行直接数值求解,对小尺度的涡建立相应的模型(亚格子模型)来封闭。虽然大涡模拟方法对计算的要求较高,但是,其与直接数值模拟相比,计算量要小很多,且比雷诺平均方法(RANS)求解精确,因此,大涡模拟方法的应用较为广泛。
1.1 连续相控制方程
将N-S方程无量纲化并进行过滤运算,可以得到湍流大涡模拟的连续方程和动量方程为:

过滤后的亚网格应力是未知的,需要建立专门的模型对上述方程封闭。封闭模型采用基于涡黏性假设的Smagorinsky-Lilly模型,网格过滤尺度Δ=1/3V,V 为计算单元的体积。
1.2 离散相控制方程
采用离散相模型(DPM),通过积分拉氏坐标系下的颗粒作用力微分方程来求解离散颗粒的轨迹。在求解过程中,仅考虑颗粒重力及相间曳力,其控制方程为

计算中采用球形曳力模型:

式中:Re为雷诺数;a1,a2,a3为实验常数。
2
模型选择
2.1 几何模型
实验系统示意图如图1所示。数值模拟对象为形成射流的入口细长圆管段(内径1.6mm,外径2.0mm,长70mm)、长方体水槽(40mm ×40mm×200mm)和出口圆管段(内径1.6mm,外径2.0mm,长20mm),入口圆管段伸入水槽长度为50mm,如图1中标号3所示。几何模型如图2所示。

图1 实验系统示意图

图2 计算区域几何模型图
采用结构化网格对计算区域进行网格划分,横向和高度方向采用非均匀网格,计算区域由内向外的网格由密变疏,如图3所示。最大与最小网格尺度比为1.2,纵向采用均匀网格.计算域中心的网格约为0.3mm×0.3mm×0.5mm,网格总数约为329万,网格过滤尺度Δ=0.35mm。

图3 计算区域网格示意图
2.2 计算模型
连续相采用LES方法和Smagorinsky-Lilly亚网格尺度模型进行求瞬态求解,在进行流场模型验证以及聚苯乙烯颗粒的跟随性分析时,连续相和离散颗粒相时间步长均为10-4s.在进行颗粒模型验证即虚拟颗粒运动模拟时,考虑到响应时间的长短,连续相和离散颗粒相时间步长均设置为10-8s。进、出口边界条件分别设置为速度入口和压力出口,由于入口处为管内层流,因此,速度入口湍流参数设置为无扰动。离散相模型设置颗粒注射方式为单点注射,瞬态追踪,时间步长与连续相一致,并设置所有颗粒的初始状态都相同,只考虑重力和曳力作用,颗粒与流体间的耦合方式为双向耦合。
3
模型验证
3.1 流场模型验证
在图1所示的实验系统中,采用IDS公司的3240cp-m黑白数字相机,镜头为可调焦远心镜头,激光器是波长650nm、功率200MW 的半导体激光器。实验时镜头的放大倍率为1倍,相机拍摄帧率为60fps,曝光时间为5ms。射流喷管直径D=1.6mm,射流雷诺数Re=886,射流管内平均速度为0.5m/s。示踪粒子为聚苯乙烯颗粒,颗粒直径为1-10μm,其Stokes数为1.8×10-5~1.8×10-3,可以认为,颗粒相的扩散率几乎等于流体相的扩散率,能够很好地跟随流体的运动。在实验中,采用移动相机的方式来拍摄射流流场的不同区域。
由于实验拍摄和数值模拟的分辨率存在差异,数值模拟无法和实验所拍摄到的流场完全一致。但是,在射流流场发展演变过程中,两者的流场结构具有相似性,流场模拟时间tf=0.1\0.5\1.0s 时两者流场结构对比如图4所示。可以认为,这里采用的大涡模拟方法能够用于圆管淹没水射流的数值模拟计算。

图4 射流流场实验结果与数值模拟结果对比图
3.2 颗粒模型验证
为了对所选取的计算模型进行验证,定义了一种与水的密度相同的虚拟颗粒,并对粒径分别为1,3,5,8,10μm的5种虚拟颗粒的速度随时间的变化规律进行理论分析和数值模拟。
当粒子由静止达到主流速度的0.99时(即粒子完全跟随流体)所用时间为
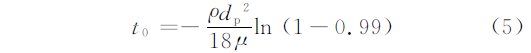
在流场模拟时间tf=1.0s时,分别将上述5种粒径的虚拟颗粒置于入口圆管段内距离入口45mm的截面中心(图2中的位置1处),颗粒初始速度为0,颗粒与流体相互作用力仅考虑曳力,连续相与离散相计算的时间步长均设置为10-8s。基于模拟结果,提取了5种不同粒径的虚拟颗粒由静止达到流场速度的99%时所用时间t′0,与采用式(5)计算得到的t″0进行对比,如表1所示。
表1 不同粒径的虚拟颗粒的响应时间

由表1可以看出,粒径为1,3μm 的颗粒的模拟结果略大于理论值,粒径为5μm及以上的颗粒的模拟结果略小于理论值。在推导理论式(5)的过程中,阻力系数Cd=24/Re,而本文在数值计算中所采用的阻力系数表达式为Morsi and Alexander的经典计算公式。当颗粒粒径较大、颗粒雷诺数大于1时,模拟采用的阻力系数比理论计算所采用的数值大。因此,模拟得到的响应时间比理论值要小。而对于小颗粒,一方面,由于计算误差造成模拟值和理论值的不完全一致;另一方面,模拟中考虑了颗粒对流体的反作用力,即考虑了颗粒对流体的影响,而在理论计算时没有考虑,因此,模拟值略偏大。但总体而言,数值模拟结果与理论分析结果基本一致,说明数值模拟结果的准确性。
由于在射流流场等存在大尺度漩涡的复杂流场中,空间位置不同,示踪粒子的速度变化程度会不同,跟随性问题也会变得复杂.本文的数值模拟选取了射流发展过程中tf=1.0s时的一个漩涡区,在漩涡周围的某一空间点处加入无质量颗粒(可视为质点)和粒径范围为1-400μm 的11种粒径的聚苯乙烯颗粒作为示踪粒子,并以该时刻作为颗粒的初始时刻,对其进行数值模拟(下文中出现的时间均为颗粒停留时间).模拟得到的不同颗粒速度和当地流体速度的偏差如图5所示.图5(a)~5(l)分别为不同时刻质点与粒径为1,5,10,15,25,50,75,100,200,300,400μm的聚苯乙烯颗粒的速度与当地流体速度的速度偏差。

图5 颗粒速度与当地流体速度偏差随时间的变化
图6为不同颗粒在不同时刻的颗粒位置及周边流场分布。

图6 不同时刻不同粒子的空间位置及周边流场分布
图5可以看出,对于较小粒径的聚苯乙烯颗粒,甚至1μm的颗粒,某些时刻的速度偏差依然会达到20%左右,而对应这些时刻(如0.9s和1.2s)的颗粒周围的局部流场区域(见图6)正是流场空间分布极不均匀的区域。这一现象说明,在剧烈变化的复杂流场中,颗粒的跟随性会变差.因此,在复杂流场中,需要对具体的流场结构进行具体分析,以了解示踪粒子在一定时间和空间内的跟随特性。
随着颗粒粒径的增大,颗粒与流体的速度偏差也呈现出增大的趋势.由图5可知,粒径范围在1-200μm的聚苯乙烯颗粒在整个运动过程中的速度偏差整体在20%以下;而当聚苯乙烯颗粒的粒径在300μm甚至更大时,速度偏差整体较大,甚至大部分时刻的速度偏差在20%以上。由图6也可以看出,在计算初始时刻,所有颗粒的空间位置和初始流场是完全一样的;随着时间的推移,小粒径的颗粒还能保持和质点接近的轨迹,而对于300,400μm的颗粒,在0.9s以后的轨迹已经和质点轨迹相差非常大,未能跟随射流的卷吸运动进入主流区。
考虑到示踪特性主要表征的是颗粒与局部周围流体速度的一致性,且在实验测量中所采用的单帧长曝光图像方法是在较短时间内(微秒至毫秒的量级)获取颗粒速度,另外,结合背光成像测量方法对示踪粒子粒径选取应尽量大的需求,对于介质为水的射流流场的示踪,若采用聚苯乙烯颗粒,推荐颗粒粒径范围选择在200μm以内.
对不同粒径的聚苯乙烯颗粒在射流中的跟随特性进行数值模拟研究,得出以下结论:
构建的大涡模拟流场模型和离散相模型能够准确地模拟出示踪粒子的响应时间,能够用于示踪粒子跟随特性的研究.
复杂流场的剧烈变化会使颗粒跟踪效果变差,需要对局部的射流流场结构进行具体分析,从而确定颗粒的跟随特性.
考虑到背光成像测量方法要求示踪粒子粒径的选取应尽量大,但跟随性要求又希望其尺寸尽量小的情况,因此,对所研究的介质为水的射流流场工况,若采用聚苯乙烯颗粒,推荐颗粒粒径范围选择在200μm以内.
参考文献
[1]崔尔杰,洪金森.流动显示技术及其在流体力学研究中的应用[J].空气动力学学报,1991,9(2):190-199.
[2]金光,焦晶晶,吴晅.典型流场测速技术应用研究进展[J]矿山机械,2015,43(12):10-15.
[3]PAFFEL M,WILLERT C E,KOMPENHANS J.Particleimage velocimetry:apractical guide[M].Berlin:Springer-Verlag,1998.
[4]梁桂华,赵宇.内燃机燃烧室流场PIV测试中示踪粒子跟随性分析[J].大连理工大学学报,2004,44(5):662-665.
[5]刘洪,陈方,励孝杰,等.高速复杂流动PIV技术研究实践与挑战[J].实验流体力学,2016,30(1):28-42.
[6] HJELMFELT A T J R,MOCKROS L F.Motion ofdiscrete particles in a turbulent fluid[J].Applied Scientific Research,1966,16(1):149-161.
[7] 沈钧涛,陈十一.球形粒子在流体中的跟随性[J].空气动力学学报,1989,7(1):50-58.
[8] 黄社华,魏庆鼎.激光测速粒子对复杂流动的响应研究—Ⅱ典型流场中粒子跟随性的数值分析[J].水科学进展,2003,14(1):28-35.
[9] 李恩邦,李志平,李淳,等.湍流中示踪粒子跟随性的数值分析[J].仪器仪表学报,2009,30(2):225-231.
[10] 王宜,顾伯勤,邵春雷.基于Lagrange算法的熔盐泵叶轮内稀疏颗粒的跟随性分析[J].南京工业大学学报(自然科学版),2016,38(1):50-55.
[11] 张乐禄.示踪粒子跟随性在离心泵内流场PIV测试研究[J].中国高新技术企业,2015(29):18-19.
[12] 张晶晶.基于单帧单曝光图像法的多相流速度场和粒度分布测量研究[D].上海:上海理工大学,2011.
[13] 陈晶丽,李琛,蔡小舒,等.流动多参数场的单帧图像法测量方法研究[J].实验流体力学,2015,29(6):67-73.
[14] 王汉青,王志勇,寇广孝.大涡模拟理论进展及其在工程中的应用[J].流体机械,2004,32(7):23-27.
[15] 苏铭德,黄素逸.计算流体力学基础[M].北京:清华大学出版社,1997.
[16] ZANG Y,STREET R L,KOSEFF J R.A dynamic mixedsubgrid-scale model and its application to turbulent recirculating flows[J].Physics of Fluids,A:FluidDynamics,1993,5(12):3186-3196.
[17] 朱赠好,周骛,蔡小舒.射流卷吸微米级结构的图像可视化研究[J].工程热物理学报,2014,35(6):1123-1126
[18] MORSI S A,ALEXANDERAJ.An investigation ofparticle trajectories in two-phase flow systems[J].Journal of Fluid Mechanics,1972,55(2):193-208.
[19] FAN Q L,ZHANG H Q,GUO Y C,et al.Studies on theeffects of stokes number in a twophase round turbulent jet[J].Journal of Combustion Science andTechnology,1999,5(4):435-440.
[20] 李志平.激光粒子图像测量中示踪粒子特性及实验方法研究[D].天津:天津大学,2007.




