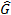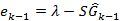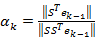气固流化床反应器广泛应用于多个过程工程行业,但由于涉及的气固两相流动复杂,迄今为止,其操作和放大还依赖于经验,这不可避免地带来了效率低、高能耗及高污染的问题。因此,研究气固流化床反应器内流体力学行为对深入理解其流动规律,进而指导操作和放大具有十分重要的意义。
通常,研究气固流化床两相流动的方法可分为理论分析、数值模拟和实验测量三大类。尽管理论分析和数值模拟可以在多尺度范围揭示流化床内的流体力学规律,其正确性需要可靠的实验测量进行验证。另外,对于开车运行的流化床反应器,测量其内部流动状态以达到故障诊断的目的对于确保生产过程的顺利进行十分重要。
伴随着气固流态化技术的发展,衍生出了多种测量气固流化床流体力学行为的技术。根据所使用的传感器是否会侵入到所测量的反应器内部,这些技术可以分为侵入式和非侵入式两类。
侵入式测量技术典型应用有压力或压差测量技术、电容探头测量技术及光纤探头测量技术等。这些技术的优点是测量速度快、成本低廉且容易实施,但由于基于单点测量,只能提供局部流动信息。另外,侵入式特性也使得传感器会对周围的流场造成一定的干扰。 非侵入式测量技术,如光学摄影技术和过程层析成像技术等,可以不与反应器内物料直接接触而提供关于流场更为丰富的信息,但价格昂贵,并且需要较为复杂的后处理过程。源于医学层析成像的过程层析成像技术,可以通过不同的“视角”“透过”不透明的反应器内部从而以图像的形式重现气固两相分布,在流化床及其它多相流系统中有广阔的应用前景,并得到广泛关注。 根据测量频率的不同,过程层析成像技术可以分为:
高频段:
X射线成像(X-CT)
核磁共振成像(Magnetic ResonanceImaging, MRI)
……
低频段:
电容层析成像(Electrical CapacitanceTomography, ECT)
电阻层析成像(Electrical ResistanceTomography, ERT)
微波层析成像(Microwave Tomography,MWT)
……
高频段的过程层析成像技术往往具有较高的空间分辨率,但这些技术时间分辨率较低,难以用于流化床实时在线测量。相反,低频段的过程层析成像技术具有较高的时间分辨率,适宜于流化床等多相流的动态特性,但缺点在于图像的空间分辨率较低。两类测量技术的差异主要源于发射场性质的不同:高频段的过程层析成像技术采用的是波束均匀且波长很短的粒子场,可以直接穿过被测介质,因此其测量敏感性不受物质分布的影响,一般称之为硬场测量技术;而低频段的过程层析成像技术采用的是波长较长的电磁场,这类软场信号在遇到测量介质时无法直接穿透,而是会发生散射或反射,因此,其测量敏感性会随着分布的不同而发生变化。总体而言,电容层析成像是目前过程层析成像技术中最为成熟的一种,且具有无辐射、成本低廉、测量速度快、耐高温高压及可适应反应器的不同尺寸和形状等优点,堪称气固流化床反应器流动状态测量的“利器”。
电容层析成像(ECT)测量气固流化床的原理是流化床反应器内的气相和颗粒相具有不同的介电常数,通过在被测反应器外部布置阵列式测量电极,当所测区域介质浓度或分布发生变化时,会引起等效介电常数的变化,从而导致传感器测得的各电极对之间的电容值发生变化,利用相应的图像重构算法,即可由测得的电容数据投影反算得到所测区域中心位置处的介质分布情况。
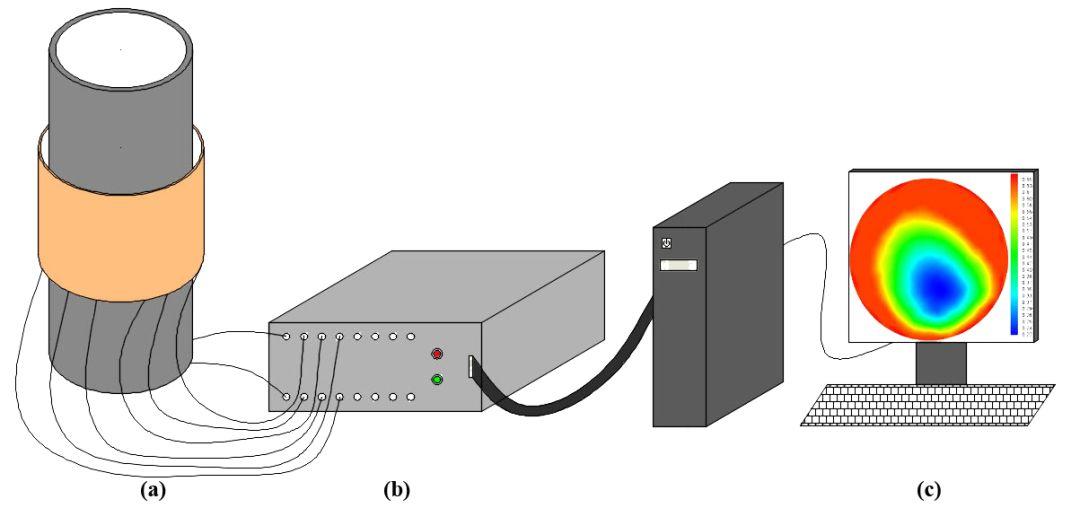
图1 电容层析成像测量系统: (a)传感器;(b)测量硬件;(c)成像计算机图1展示了一套完整的电容层析成像测量系统,由三部分组成,分别是传感器、测量硬件及成像计算机。
传感器根据测量要求布置在所测流化床反应器外壁或内壁,形成外置式或内置式传感器。传感器电极数量通常为8、12、16及24等。
图2(a)展示了典型的外置式12电极传感器示意图,其横截面视图如图2(b)所示。传感器由阵列式测量电极、轴端屏和外屏组成,其中阵列式测量电极获取由所测截面处介质浓度或分布变化而引起的电极对之间的电容值的变化,轴端屏和外屏则用于消除测量截面外的电磁信号干扰。测量硬件用于给激发电极提供激发信号,然后将其余电极与激发电极组成的电极对之间的电容值转换为电压信号,之后经过信号调节及模数转换等过程完成数据采集。成像计算机用于信号控制、数据处理及图像重构和显示等。
所谓正问题指的是在特定的电容层析成像传感器下,对测量截面特定的流型分布求解传感器各电极对之间的电容值。以图2所示的12电极电容层析成像传感器为例,在一个完整的测量过程中,首先1号电极被激发以某一电压信号,然后1-2,1-3一直到1-12电极对之间的电容值被测得;接着,2号电极被激发,2-3,2-4一直到2-12电极对之间的电容值被测得;以此类推,一直到11号电极被激发,测量得到11-12电极对之间的电容值,这样就组成了66个电容值。一般地,假设电容层析成像传感器的电极数量为l,则电容层析成像测得的独立电容数量M为M= l (l -1)/2。以上激励模式称为单电极激励。除此之外,还有多电极激励模式。比如,在双电极激励模式下,首先,1和2号电极被联合激发以某一电压信号,然后测量获得1和2号联合电极和3至12号电极组成的电极对之间的电容值;之后,2和3号电极被联合激发,然后测量获得2和3号联合电极和1号及4至12号电极组成的电极对之间的电容值;以此类推,一直到12和1号电极被联合激发,然后测量获得12和1号联合电极和2至11号电极组成的电极对之间的电容值,这样就组成了120个电容值。对于多电极激励模式,假设每次激励电极数量为l1,则电容层析成像所测得的独立电容数量M为M= l (l- l1)。根据Maxwell方程,传感器内的电场控制方程可以表述为:

其中,εr(x,y)和φ(x,y)分别为传感器测量截面内的介电常数和电势分布。公式1的边界条件为: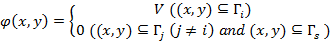
其中,Γ代表电极表面,该边界条件指当i号作为激发电极时,其表面电势强度为激发电压V,而其余电极及屏蔽均处于接地状态,即电势强度为0。通过采用高斯散度定理,各电极对之间的电容值可以按方程3计算:

其中,ε0是真空环境下的介电常数。
方程3涉及微积分,比较复杂,在实际应用时中通常将其简化为如下线性方程:

其中G是传感器测量截面内每个像素点位置的归一化介电常数值,λ是所有电极对之间的归一化电容值,G和λ分别由方程5和6计算获得:


其中,εH 和εL分别为所测固体颗粒相和气相的相对介电常数,CM 为任一分布下的原始电容值,CH 和CL 分别为当传感器测量截面内充满具有高介电常数的固体颗粒相和具有低介电常数的气相时的各电极对之间的电容值。获得CH 和CL 的过程称之为系统校准。对于流化床反应器的测量,二者分别对应固定床状态和空管状态各电极对之间的电容值。方程4中的S指归一化敏感场矩阵,其中矩阵中的每个元素表示当传感器测量截面内某像素点位置的介电常数由低变高时,所引起的每个电极对之间的归一化电容值的变化。敏感场的构建需要对传感器测量截面进行离散化,并通常划分为n × n的方形网格。
传感器通常是圆形的,因此,测量截面内的有效像素点个数N小于n × n。n或者N的选择需要权衡重构图像的分辨率和电容层析成像图像重构逆过程需要求解的未知变量的数量。对于12电极传感器而言,通常使用的网格是64 × 64的方形网格,其保留在圆形测量截面内的有效像素点数量为3228,如图2。
一种根据定义直接依次将传感器测量截面内每个像素点的介电常数由低变高,并通过仿真或者实验获得每一次变化引起的所有电容值的变化,该方法模拟耗时,对于实验测量,因为涉及到每个像素点位置的精确调控,难度较大。
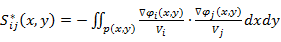
其中, 是编号为i 和j 的电极组成的电极对在位置为p(x,y)处的像素点的敏感度,φi (x,y)和φj (x,y)分别是编号为i 和j 的电极分别被大小为Vi 和Vj 的电压激发时测量截面内的电势分布。通过公式7获得的S*需要根据下式进行归一化:
是编号为i 和j 的电极组成的电极对在位置为p(x,y)处的像素点的敏感度,φi (x,y)和φj (x,y)分别是编号为i 和j 的电极分别被大小为Vi 和Vj 的电压激发时测量截面内的电势分布。通过公式7获得的S*需要根据下式进行归一化:

这里的Smn和  分别表示S和S*在第m行和第n列的元素。M个电极对都有相对应的敏感场,但对于一般的圆形传感器,只有
分别表示S和S*在第m行和第n列的元素。M个电极对都有相对应的敏感场,但对于一般的圆形传感器,只有  个不同的敏感场,其余敏感场可通过旋转或者镜像这
个不同的敏感场,其余敏感场可通过旋转或者镜像这  个敏感场获得。
个敏感场获得。由于电容层析成像的软场特性,敏感场会随着测量截面内介电常数分布的不同而发生变化,但一般真实分布是未知的,所以为了方便,通常将在传感器内不含有任何物质,即真空环境下计算获得的敏感场作为标准敏感场进行使用。
图3(a)和3(b)分别展示了12电极电容层析成像传感器相邻和相对电极对的敏感场分布,所有电极对的平均敏感场如图3(c)所示。可以看到,敏感场的分布极不均匀,尤其在中心测量区域,敏感场很低,甚至有负值的出现。
和正问题过程相反,电容层析成像的逆问题指在已知传感器各电极对之间的电容值的情况下,通过一定的图像重构算法重构出测量截面内的介电常数分布,即G=S-1λ。然而,电容层析成像的图像重构过程有两个难点。首先,测得的电极对之间的电容值的数量远少于重构图像的像素点数量,比如,对于12电极传感器单电极激励模式,电容值的数量为66个,而需要重构的像素点的数量有3228个,因此该过程属于典型的不适定问题,即S-1不存在。另外,电容层析成像重构过程的病态特性使得重构的图像质量对测量值的噪音敏感。为解决这些问题,研究者们提出了很多不同的算法,可分为两大类,即单步法和迭代法。其中最常用的单步算法有线性反投影算法和Tikhonov正则化算法,最常用的迭代算法是Landweber迭代算法。线性反投影算法是电容层析成像领域提出的最早的算法,其原理是以S的转置代替其本不存在的逆,如方程9所示:

其中, 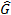 是重构的介电常数分布,uλ 是元素全部为1并且维度和λ一致的向量。
是重构的介电常数分布,uλ 是元素全部为1并且维度和λ一致的向量。 线性反投影算法中的归一化相当于每个像素点的灰度值先后由分子及分母部分分别算一遍,然后分子获得的灰度值在每个像素点处被分母获得的相应位置处的灰度值除以重新调整缩放其值。
Tikhonov正则化算法方程如下:

其中,μ 是取值为较小正数的正则化参数,I是维度为N× N的单位矩阵。μ 的取值在很大程度上会影响Tikhonov正则化算法求解逆问题的解的准确性。理论上,L-曲线法及广义差分原理可以用于确定对特定的流型分布较适宜的μ值。但一般来讲,这些方法都比较复杂,实用性较差。因此,μ 通常通过试错的方法获得。
一般来讲,要获得高质量的图像,必需使用迭代类算法。Landweber迭代算法是迭代类算法中最常用的一种,其方程如下:


其中,k是迭代步数,α是迭代步长,一般取值1~2,ek−1是实际测得的电容与通过在第(k−1)次迭代中重构的介电常数分布由正问题计算获得的电容之间差值,即
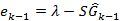
Landweber迭代算法的初步估计值通常由方程9所示的线性反投影算法获得。Landweber迭代算法最大的缺点在于它的半收敛特性,为了提高其收敛速度,步长因子依据下式进行改变:
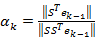
Landweber迭代算法的终点判据有两种方法,第一种是预设迭代次数,如200次;另一种是通过公式15判断相邻两次重构图像之间的距离是否小于预设的值,如0.01,需要说明的是该值并非越小越好。

在获得测量截面的介电常数分布之后,还需要经过浓度模型转换为测量截面的各相浓度分布图像。目前常用的有四种浓度模型(定义下表所示),分别是:
表中,  是重构图像中的归一化固体颗粒相体积浓度,且在流化床处于空管状态时取值为0,在流化床处于固定床状态时取值为1。Kr是流化床内固相颗粒和气相相对介电常数的比值。
是重构图像中的归一化固体颗粒相体积浓度,且在流化床处于空管状态时取值为0,在流化床处于固定床状态时取值为1。Kr是流化床内固相颗粒和气相相对介电常数的比值。
图4展示了当Kr=3时不同浓度模型计算的归一化颗粒相体积浓度。可以看到,四种浓度模型中,并联模型计算的归一化颗粒相体积浓度的数值与归一化介电常数相同,逆Maxwell模型计算的归一化颗粒相体积浓度小于归一化介电常数,而串联模型和Maxwell模型计算的归一化颗粒相体积浓度大于归一化介电常数。一般在流化床的测量中,并联模型使用最广。获得归一化颗粒相浓度分布后,结合满管状态即固定床下的固相体积分数,即可获得测量截面的颗粒相浓度分布,即: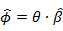
其中,θ是固定床状态下的固相体积分数。
未 完 待 续
以上主要介绍了电容层析成像测量原理及成像模型,后续将继续介绍电容层析成像测量流化床关键流体力学参数及相关应用。


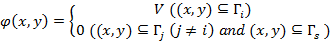




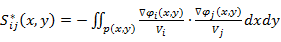
 是编号为i 和j 的电极组成的电极对在位置为p(x,y)处的像素点的敏感度,φi (x,y)和φj (x,y)分别是编号为i 和j 的电极分别被大小为Vi 和Vj 的电压激发时测量截面内的电势分布。通过公式7获得的S*需要根据下式进行归一化:
是编号为i 和j 的电极组成的电极对在位置为p(x,y)处的像素点的敏感度,φi (x,y)和φj (x,y)分别是编号为i 和j 的电极分别被大小为Vi 和Vj 的电压激发时测量截面内的电势分布。通过公式7获得的S*需要根据下式进行归一化:
 分别表示S和S*在第m行和第n列的元素。M个电极对都有相对应的敏感场,但对于一般的圆形传感器,只有
分别表示S和S*在第m行和第n列的元素。M个电极对都有相对应的敏感场,但对于一般的圆形传感器,只有  个不同的敏感场,其余敏感场可通过旋转或者镜像这
个不同的敏感场,其余敏感场可通过旋转或者镜像这  个敏感场获得。
个敏感场获得。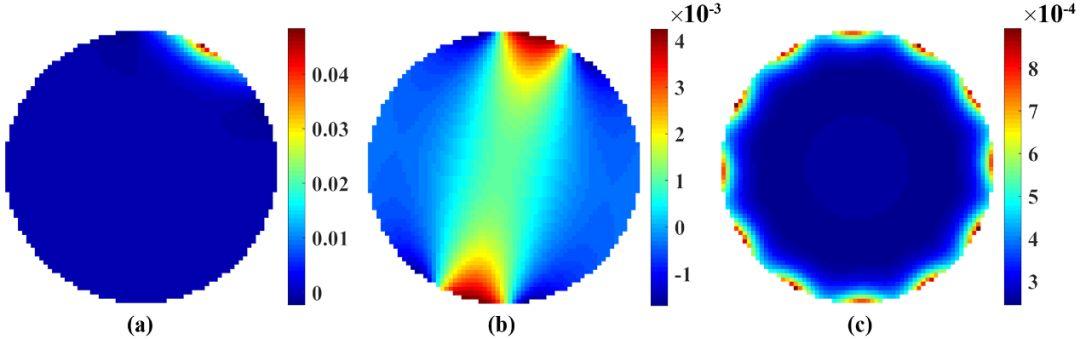
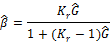

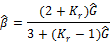

 是重构图像中的归一化固体颗粒相体积浓度,且在流化床处于空管状态时取值为0,在流化床处于固定床状态时取值为1。Kr是流化床内固相颗粒和气相相对介电常数的比值。
是重构图像中的归一化固体颗粒相体积浓度,且在流化床处于空管状态时取值为0,在流化床处于固定床状态时取值为1。Kr是流化床内固相颗粒和气相相对介电常数的比值。
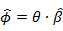
![]()