清华笔记：计算共形几何讲义 （8）狭缝映射（Slit Map）的存在性

顾险峰 纽约州立大学石溪分校

计算机与应用数学系 终身教授

我们用较为初等的复变函数方法证明一种共形映射的存在性：狭缝映射（slit mapping）。如图所示，给定亏过为0的多连通曲面，存在共形映射将其映射到平面区域，每个边界的联通分支都被映成一条狭缝（slit）。这里所用的数学证明方法比较巧妙，令人赏心悦目。真正的计算和需要应用全纯微分的方法。这篇笔记和罗锋教授讨论过。

在复平面上，复数，平面的Lebesgue测度为，面元为

。

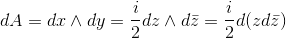引理：假设J是一条Jordan曲线，是某个Jordan区域的边界，解析映射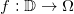为1-1映射，那么

。

证明：Jordan区域的面积为

，

代入，我们得到

。

定理（Gronwall）假设平面区域包含无穷远点，解析映射为1-1映射，并且具有Laurent级数表示，

,

令，那么

。

证明：假设，令，应用上面引理，

由于，我们得到

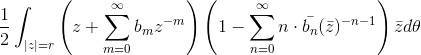
进一步化简，得到

直接计算得到：

，

然后，令，得到结论。证明完毕。

推论 1：假设平面区域包含无穷远点，解析映射为1-1映射，并且具有Laurent级数表示，

,

那么 。极值情况，当且仅当

这等价于的补集是一条长度为的水平线段。

证明：令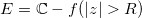，解析映射为1-1映射，因此。由以上定理，我们得到。极值情况，直接计算可得。证明完毕。

定理（Breberbach）解析函数（1-1映射）族

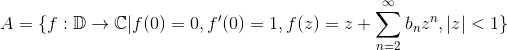
中所有的函数都有。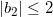

证明：给定，构造

,

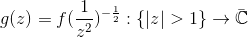那么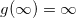，在单位圆外是解析1-1映射。我们计算的Lauren展开，

由上面推论，我们得到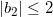。证明完毕。

定理 （Koebe - 1/4）解析函数（1-1映射）族

，

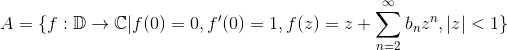如果，那么

。

证明：设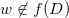，考虑

,

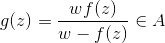考虑在0点的Tayler展开:

,

直接计算表明

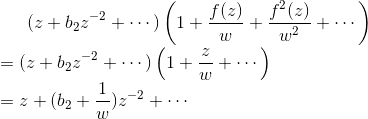
由Breberbach定理，我们得到

由此，所以。证明完毕。

推论2：假设解析1-1映射

,

那么

。

证明：考虑，证明完毕。

定义：复平面上的区域被称为是狭缝区域（slit domain），如果其边界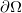的每个联通分支或者是一个点，或者是水平闭区间。

引理1：在点附近，解析函数

那么

。

定理（Possel-Gronwall）： 复平面上的一切区域都和平面狭缝区域共形等价。

定理（Hilbert）： 复平面上的一切区域，其边界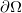具有有限个联通分支，都和平面狭缝区域共形等价。

证明：给定一个平面区域，我们用Mobius变换，可以假设并且， 令解析1-1映射族

，

令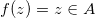，所以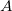是非空集 合。由推论2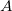，是一个正规函数族，（normal family）。由正规函数族的紧性，函数序列的极限也在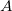中。所以，存在，使得

,

我们欲证明 是一个狭缝区域。

图1. 构造狭缝映射（slit map）。

若反之，则存在的一个联通分支，既不是一个点，也不是一条水平线段。我们可以构造一个映射，构造方法如下：

如图1所示，我们构造黎曼映照的逆映射：

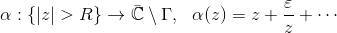
和狭缝映射：

。

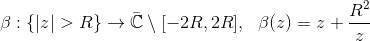则复合映射：

由推论1，比较，它们将圆盘的补集映到平面区域，狭缝映射的实部取到最大，因此

,

由引理1，，我们得到：

,

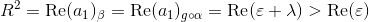由此，我们得到。

由此，由引理1，在上，复合映射

由，我们得到,  这和的取法矛盾，因此假设错误，结论成立。证明完毕。

后面我们会详细解释狭缝映射（Slit Map）的算法，主要的理论工具是全纯1-形式。