基于权函数法的应力强度因子计算

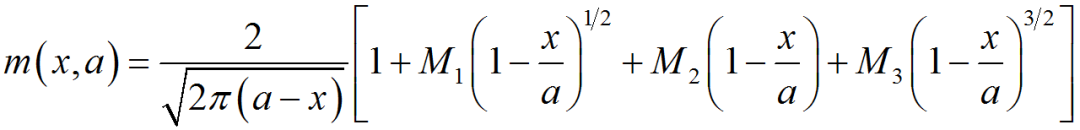
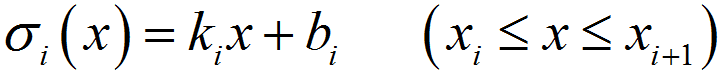
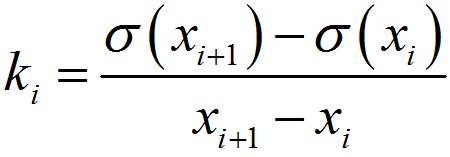
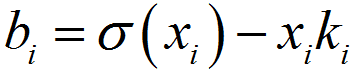
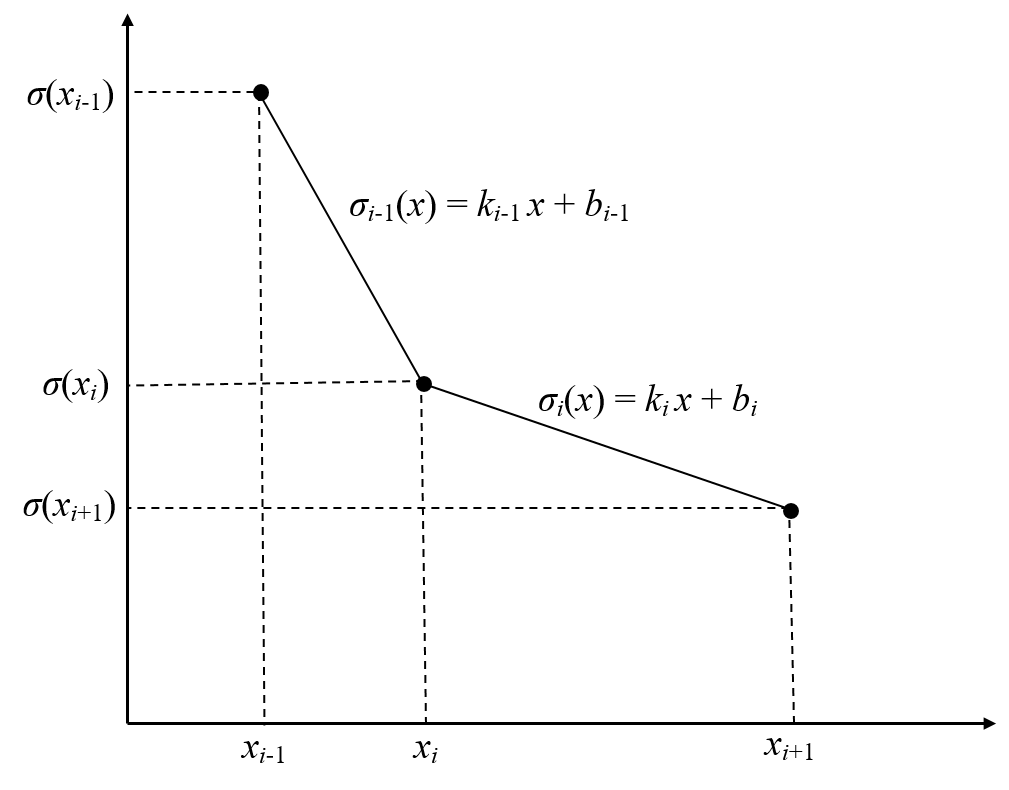
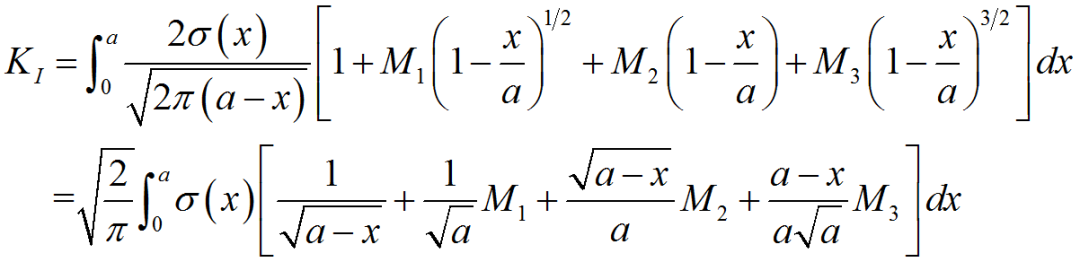
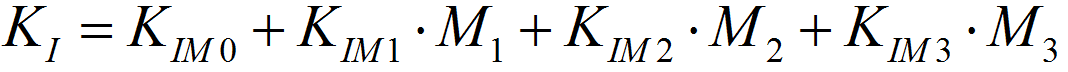
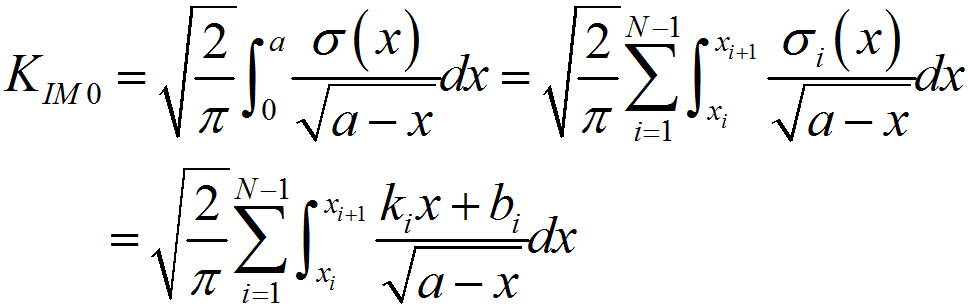
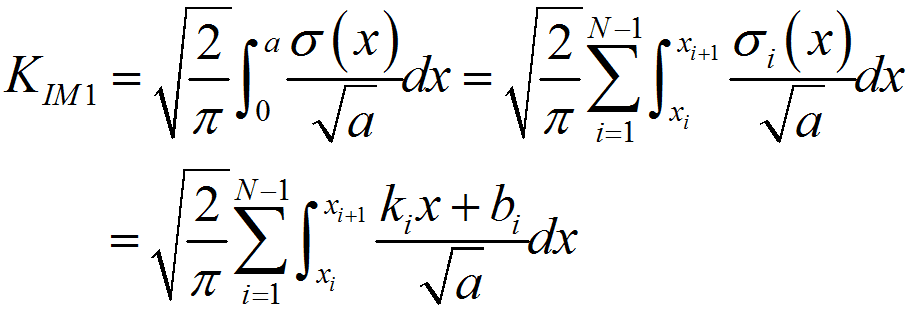

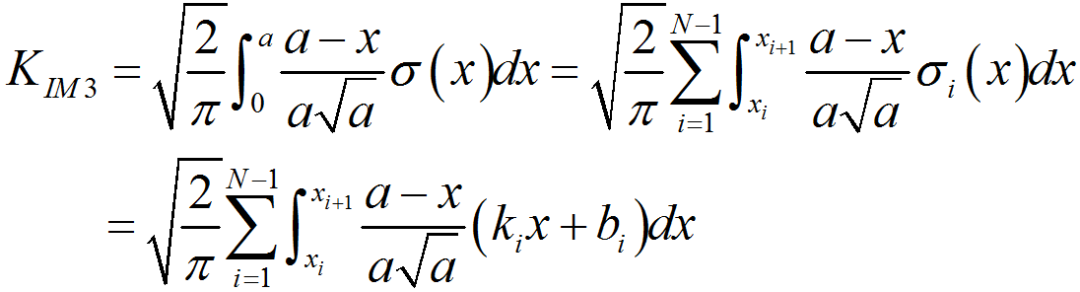

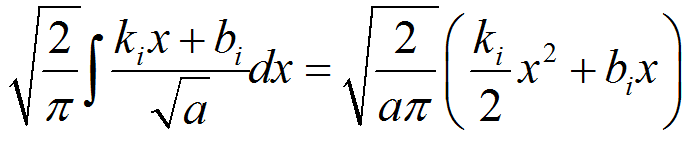

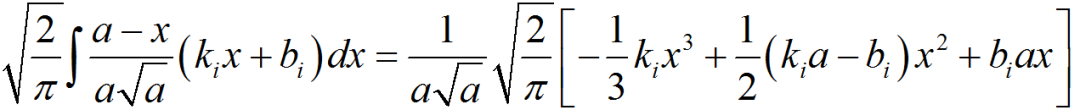
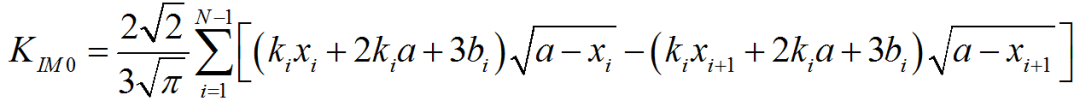
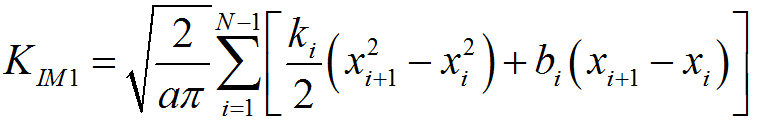
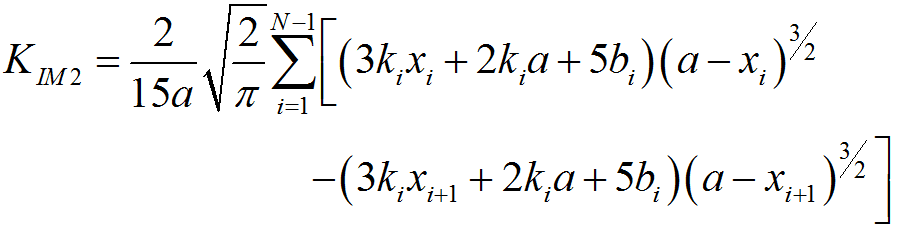
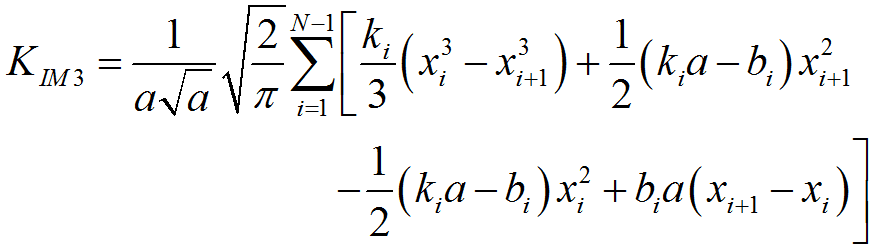



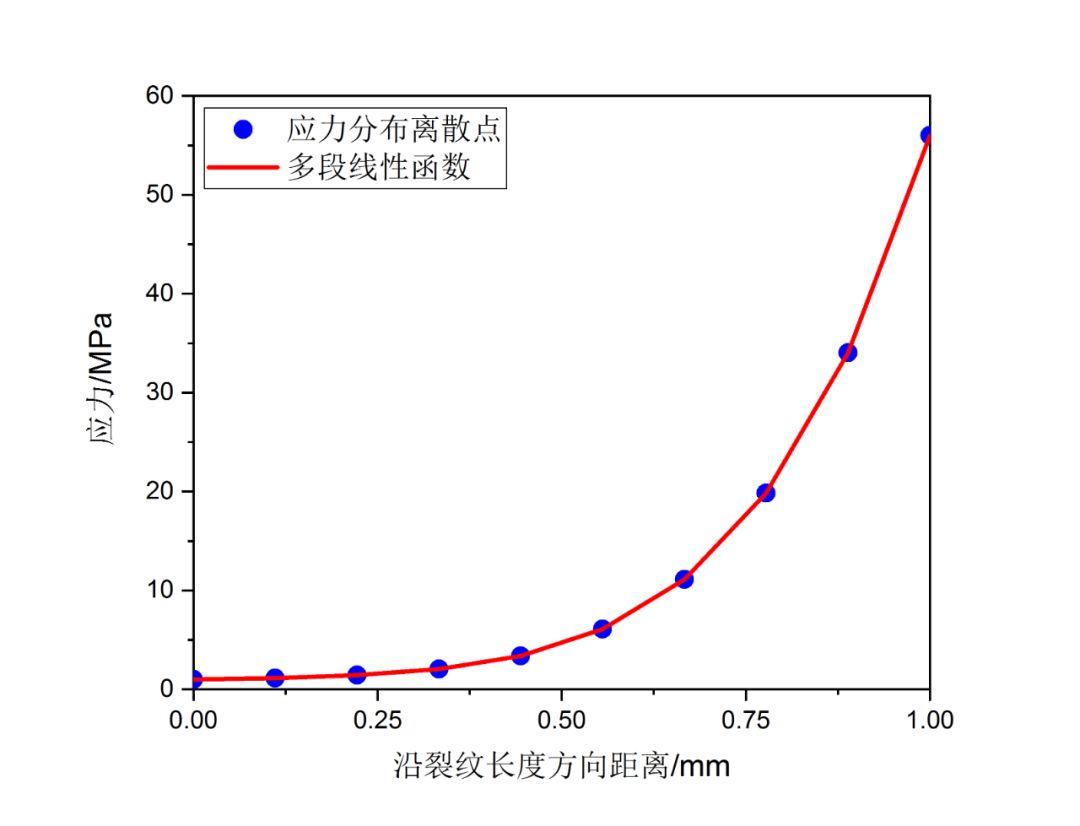
%程序用于计算半无限大平板中角裂纹的应力强度因子clear,clca=1; %裂纹长度stress0=1; %远场应力discrete_num=500; %离散积分点数x=linspace(0,a,discrete_num);stress=stress0*(1+x./a+2*(x./a).^2+4*(x./a).^3+16*(x./a).^4+...32*(x./a).^5);%采用多段线性函数离散化应力分布stress_discrete=zeros(discrete_num,1); %存放离散化后的应力line_func_k=zeros(discrete_num-1,1); %多段线性函数系数kline_func_b=zeros(discrete_num-1,1); %多段线性函数系数bfor i=1:discrete_num-1 %计算多段线性函数系数line_func_k(i)=(stress(i+1)-stress(i))/(x(i+1)-x(i));line_func_b(i)=stress(i)-x(i)*line_func_k(i);end%验证多段线性函数正确性stress_discrete(1)=stress(1);for i=2:discrete_numstress_discrete(i)=line_func_k(i-1)*x(i)+line_func_b(i-1);end%绘制应力分布及多段线性函数表示的应力分布figurescatter(x,stress)hold onplot(x,stress_discrete)title('应力分布及多段线性函数表示的应力分布');xlabel('沿裂纹长度方向距离/mm');ylabel('应力/MPa');legend('应力分布离散点','多段线性函数');%计算应力强度因子weight_func_M1=0.0719768; %权函数系数weight_func_M2=0.246984;weight_func_M3=0.514465;KIM0=zeros(discrete_num-1,1);KIM1=zeros(discrete_num-1,1);KIM2=zeros(discrete_num-1,1);KIM3=zeros(discrete_num-1,1);for i=1:discrete_num-1KIM0(i)=2*sqrt(2)/(3*sqrt(pi))*((line_func_k(i)*x(i)+2*line_func_k(i)*a+...3*line_func_b(i))*sqrt(a-x(i))-(line_func_k(i)*x(i+1)+...2*line_func_k(i)*a+3*line_func_b(i))*sqrt(a-x(i+1)));KIM1(i)=sqrt(2/(a*pi))*(line_func_k(i)/2*(x(i+1)^2-x(i)^2)+...line_func_b(i)*(x(i+1)-x(i)));KIM2(i)=2/(15*a)*sqrt(2/pi)*((3*line_func_k(i)*x(i)+2*line_func_k(i)*a+...5*line_func_b(i))*(a-x(i))^(3/2)-...(3*line_func_k(i)*x(i+1)+2*line_func_k(i)*a+...5*line_func_b(i))*(a-x(i+1))^(3/2));KIM3(i)=1/(a*sqrt(a))*sqrt(2/pi)*(line_func_k(i)/3*...(x(i)^3-x(i+1)^3)+1/2*(line_func_k(i)*a-line_func_b(i))*...x(i+1)^2-1/2*(line_func_k(i)*a-line_func_b(i))*x(i)^2+...line_func_b(i)*a*(x(i+1)-x(i)));endKIM0_sum=sum(KIM0);KIM1_sum=sum(KIM1);KIM2_sum=sum(KIM2);KIM3_sum=sum(KIM3);K=KIM0_sum+KIM1_sum*weight_func_M1+KIM2_sum*weight_func_M2+...KIM3_sum*weight_func_M3;

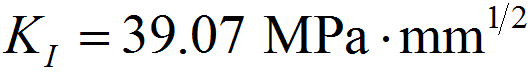
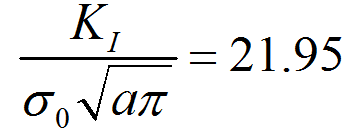

登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2023-05-30
最近编辑:1年前
还没有评论
相关推荐
最新文章
热门文章




