利用Abaqus UEL开发自定义单元2
本文是关于利用Abaqus UEL开发自定义单元系列的第二篇,这里我们将继续以线性3节点三角形平面单元为例,讨论平面单元在Abaqus UEL用户子程序中的实现方法,并利用Abaqus内置单元CPS3进行验证。
1. 线性3节点三角形平面单元的构造
1.1 单元的几何和节点描述
3节点三角形单元如图1.1所示,3个节点沿逆时针分别编号为1,2,3,各自的位置坐标为 ,i=1,2,3,各个节点的位移(分别沿x方向和y方向)为 ,i=1,2,3。因此,每个节点有2个位移自由度,整个单元共有6个位移自由度。
将所有节点上的位移组成一个列阵,记为 ;同样,将所有节点上受到的节点力也组成一个列阵,记为 ,因此:

1.2 单元位移场的表达
如果将x方向和y方向的位移进行分别表达,则每个方向的位移将由3个节点位移来确定,即每个方向的位移可设定为3个待定系数。考虑到简单性、完备性(completeness)、连续性(Continuity)及待定系数的唯一确定性原则,分别选取单元中各个方向的位移模式为:
注意,在构造位移模式时必须考虑位移模式的完备性以及连续性,否则单元的结果是不收敛。单元收敛意味着随着单元尺寸的减小,有限元法给出的近似解应该是趋近于真实解。
由节点处 的位移值 ,有:
将其带入上式可以解出待定系数。随后可以将位移函数重新以三个节点处的节点位移的形式表示出来:
其中 被称为形函数(shape function)。
将上式表示为矩阵形式有:
其中 为形函数矩阵,即:
而
其中系数 , , 和A分别为:
可以看到,这里的A实际上为三角形的面积。
这里解释一下形函数的作用。从上式可以看出,只要给出了单元三个节点处的位移值,则该单元区域内任意位置处的位移值都可以通过形函数与节点位移的乘积之和来获得,因此形函数实际上起到了与插值类似的作用。同理,如果知道了节点处的应变值 (或其它的单元基本变量),则单元任意位置处的应变值ε同样可以通过形函数来获得:
此外,形函数还具有一个非常重要的性质:在形函数下标对应的节点处取值为1,而在其余所有节点处的取值均为0,例如在图1.2中,在节点1的形函数N1在节点1处取值为0,而在其他节点处取值为0。换句话说,这意味着形函数具有Kronecker delta函数的性质,即:

此外,从图1.2中还可以看出,在单元区域内形函数的取值构成了一个平面,这显然是由于形函数中仅包含了x和y的线性项,这意味在单元边上,形函数的取值呈线性变化。
1.3 单元应变场的表达
由弹性力学平面问题的几何方程(矩阵形式)有:
其中[∂]为几何方程的算子矩阵。
将位移场表达式带入上式可得到应变的表达式为:
其中 被称为几何函数矩阵,可表示为:
带入形函数表达式,可以将几何函数矩阵 以节点坐标的形式表示出来:
其中:
1.4 单元应力场的表达
由弹性力学中平面问题的物理方程,将其写为矩阵形式为:
其中 为平面应力问题的弹性系数矩阵:
对于平面应变问题,弹性系数矩阵D可表示为:
带入应变矩阵 ,有:
其中S为应力函数矩阵:
1.5 单元势能的表达
通过上面推导,单元的三大基本变量 均以基于节点位移列阵 的形式表达了出来,将其带入单元势能的表达式中,有:
上式中b和p分别为作用在单元上的体力和面力, 为单元刚度矩阵,可表示为:
其中t为平面单元的厚度。由于B矩阵和D矩阵均为常系数矩阵,因此上式中的积分可以直接解出:
其中各个子块矩阵为:
其中:
对于等参单元,刚度矩阵中的积分往往无法通过解析方法来获得,一般需要通过高斯积分法来获得数值解。
1.6 单元的刚度方程
根据最小势能原理,将单元的势能对节点位移 取一阶变分,有:
由于 的任意性,因此有:
上式即为单元的刚度方程,这是一个线性方程组,可以直接通过数值方法进行求解。
2. 平面单元在UEL中的实现
对于诸如UEL和UMAT等较为复杂的子程序,为了便于调试程序,一般不会直接将自定义单元或自定义材料应用到复杂的有限元模型上,而是采用最简单的有限元模型(如单个单元的模型)对用户子程序进行调试,当确认无误后再逐步增加模型或子程序的复杂程度。因此,本文首先通过手动计算的方式完成单个平面单元的计算算例,获得平面单元的刚度矩阵以及单元应力结果。随后通过UEL子程序编写平面应力单元,并利用算例给出的刚度矩阵验证程序的正确性。
2.1 单个平面单元的计算流程
假定在平面应力条件下,计算如图2.1所示的单元的刚度矩阵。所示坐标的单位为毫米。令E=210GPa,v=0.25,厚度t=20mm。假定将单元节点1和节点3的位移自由度约束,并在节点2的x方向施加100N的节点力,试确定单元应力。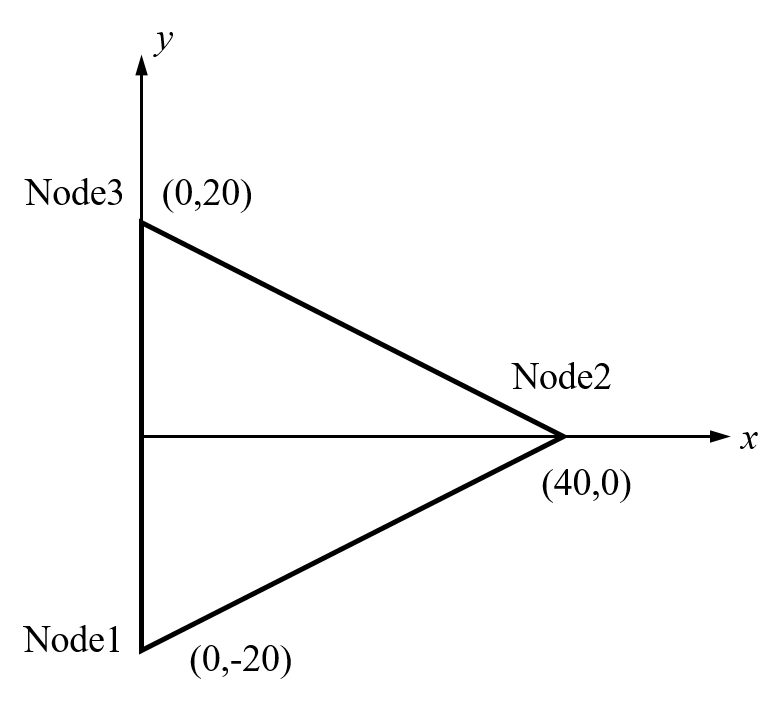
参考前面的推导,为了计算单元刚度矩阵K,需要首先计算几何函数矩阵B和弹性系数矩阵D。而计算几何函数矩阵B需要用到单元面积A以及参数ai, bi和ci(i=1,2,3)。参考前面推导的公式,可得各个参数的值为:
带入可得几何函数矩阵B为:
对于本例研究的平面应力问题,其弹性系数矩阵D为:
最终得到单元的刚度矩阵K为:
带入位移边界条件和载荷边界条件,则单元的节点位移列阵q和节点力列阵P可表示为:
因此该问题等价于求解刚度方程中的未知量:
在前面的文章中已经提到,由于刚度方程中同时存在未知节点力和节点位移,因此需要将刚度方程进行分解。首先求解未知节点位移 和 :
解得节点列阵为:
随后将节点列阵q带入完整的刚度方程即可得到节点力列阵P为:
故单元应力为:
其中应力函数矩阵S为:
最终计算得到单元的Von Mises应力为:
2.2 UEL子程序的编写
2.2.1 矩阵乘法和矩阵转置子程序
从上面的分析流程可以看出,为了获得平面应变单元的刚度矩阵K,需要首先计算单元的几何函数矩阵B以及弹性系数矩阵D,而计算几何函数矩阵B主要用到了节点坐标参数,计算弹性系数矩阵D主要用到了材料本构参数。由于在计算过程中多次使用了矩阵乘法和矩阵转置等运算,对于这些运算,我们可以将其同样定义为子程序(类似于函数),这样在UEL子程序中需要进行这些运算时只需要要调用相应的子程序即可。
其中矩阵C中第i行第j列的元素可表示为:
注意,矩阵乘法是区分左乘和右乘的,即:
并且只有当矩阵A的列数等于矩阵B的行数时矩阵才可以相乘。
通过上述算法,可以得到矩阵乘法子程序如下所示。 需要注意的是,由于Abaqus采用了F77的Fortran版本,无法通过ALLOCATABLE声明维度可变的数值,因此必须将矩阵的维度作为输入参数传递到子程序中。在输入这些参数时,需要注意矩阵维度是否输入正确,否则可能会得到错误的结果。
需要注意的是,由于Abaqus采用了F77的Fortran版本,无法通过ALLOCATABLE声明维度可变的数值,因此必须将矩阵的维度作为输入参数传递到子程序中。在输入这些参数时,需要注意矩阵维度是否输入正确,否则可能会得到错误的结果。
对于矩阵转置运算,设A为m×n的矩阵,则称n×m的矩阵B为矩阵A的转置,记为:
其中矩阵B第i行第j列的元素可表示为:
通过上述算法,可得到矩阵转置的子程序如下所示: 这些子程序可以与UEL子程序放在同一个Fortran文件中,随后利用CALL关键字加上子程序名以及相应的输入参数即可调用相应的子程序。例如,下面一行语句通过调用矩阵乘法子程序来计算应力函数矩阵S:
这些子程序可以与UEL子程序放在同一个Fortran文件中,随后利用CALL关键字加上子程序名以及相应的输入参数即可调用相应的子程序。例如,下面一行语句通过调用矩阵乘法子程序来计算应力函数矩阵S:
其中D为弹性系数矩阵D,B为几何函数矩阵B,S为应力函数矩阵S,NNODE为单元节点数,取值为3。
2.2.2 几何函数矩阵B的计算
为了计算几何函数矩阵B,需要首先通过获取节点坐标,并通过节点坐标计算ai,bi和ci(i=1,2,3)的取值,相应的代码实现如下所示:
 其中DA,DB,DC分别用于存放参数ai,bi和ci,AREA为三角形单元的面积。
其中DA,DB,DC分别用于存放参数ai,bi和ci,AREA为三角形单元的面积。
随后即可组装得到完整的几何函数矩阵B。
2.3 单个平面单元的计算算例
基于图2.1中的计算参数,本文利用Abaqus的CPS3单元(线性3节点平面应力单元)计算得到单元的位移分布和Von Mises应力如图3.1所示,图中还给出了通过UEL子程序计算得到的位移结果作为对比。
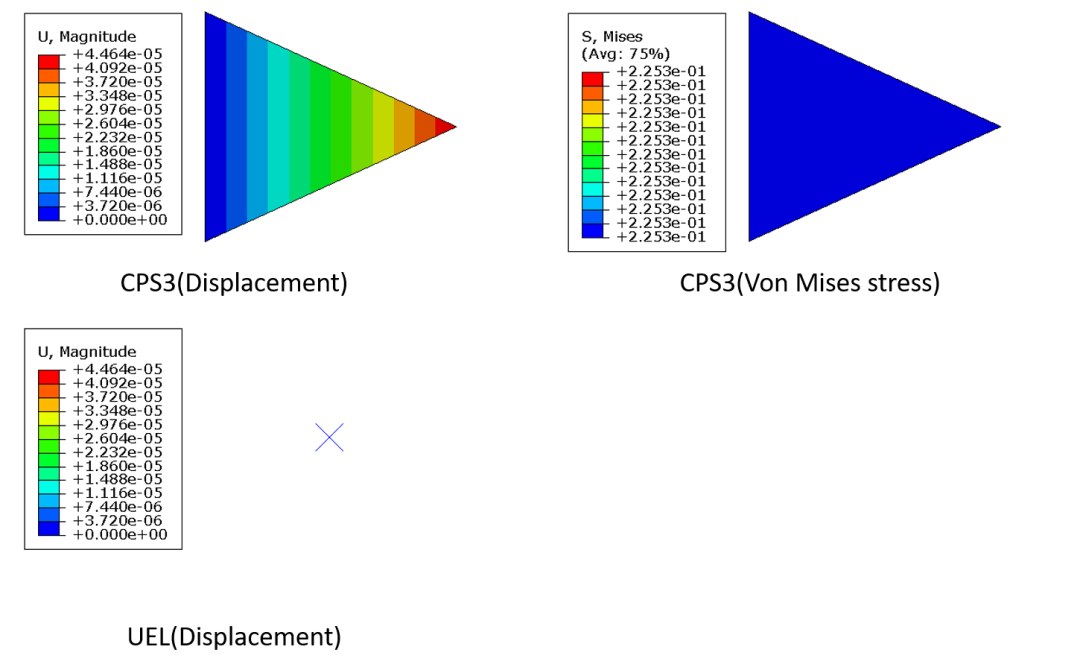
从图中可以看出,通过UEL子程序计算得到的节点位移与CPS3单元给出的计算结果完全吻合,并且CPS3单元给出的位移和单元应力也与前面手动计算得到的结果一致。此外,由于用户自定义单元中的节点数量和自由度数等信息完全是由用户指定的,可以看到Abaqus无法 正常给出单元的拓扑信息,这使得用户自定义单元的后处理非常繁琐,一般只能借助第三方后处理软件(如Matlab、Tecplot)或Abaqus二次开发才能完成。
尽管Abaqus无法给出自定义单元的网格,但是Abaqus的内置单元是可以正常显示和后处理的。因此,为了获取自定义单元的云图,我们可以在自定义单元上包覆一层与自定义单元具有相同拓扑结构的Abaqus内置单元,例如对于本文定义的3节点三角形单元,可使用Abaqus的平面单元或膜单元,但应保证节点数和自由度数是一致的。这些Abaqus内置单元与自定义单元共享节点,这意味着内置单元可以获取自定义单元的自由度值。当内置单元的刚度逐渐趋于零时,采用双层单元与仅采用自定义单元的结构的响应将趋于一致。由于内置单元可以被Abaqus正常识别,因此通过这种方法可以间接获得自定义单元的位移分布云图。由于内置单元对整个结构的刚度没有贡献,只是起到了结果后处理的作用,因此也被称为哑单元(Dummy element)。
需要注意的是,由于在Abaqus中只能输出自定义单元的节点位移(自由度),无法直接输出节点应力等结果,因此无法绘制出应力云图。如果需要在Abaqus中直接绘制这些结果,只能借助Abaqus二次开发才能完成。
下面,本文以一悬臂梁结构为例,简要介绍哑单元的实现流程。
3. 受集中载荷的悬臂梁结构
假设有一长为1m,宽度和厚度均为0.1m的悬臂梁,在悬臂梁端点处受到4000N的集中力。已知材料的弹性模量E为200GPa,试采用用户自定义单元计算悬臂梁的挠度。
由于用户自定义单元与常规单元的定义方式是完全相同的,因此我们可以首先在Abaqus中正常建立模型,并赋予Abaqus的内置单元类型,随后输出inp文件,并在inp文件中补充自定义单元的相关信息,并将内置单元的类型修改与自定义单元的单元类型,即可将模型替换为采用自定义单元计算的有限元模型。在Abaqus中建立的有限元模型如图3.1所示。

前面提到,为了实现自定义单元的后处理,需要在自定义单元上包覆一层内置单元作为哑单元。由于自定义单元与哑单元共享节点,因此我们可以直接复 制自定义单元的单元定义,并偏移的单元编号(自定义单元和哑单元不能有相同的单元编号),即可完成哑单元的定义。这里,我们选取CPS3单元作为哑单元(也可以是其他的3节点线性平面单元),在inp文中的相关定义如下所示:
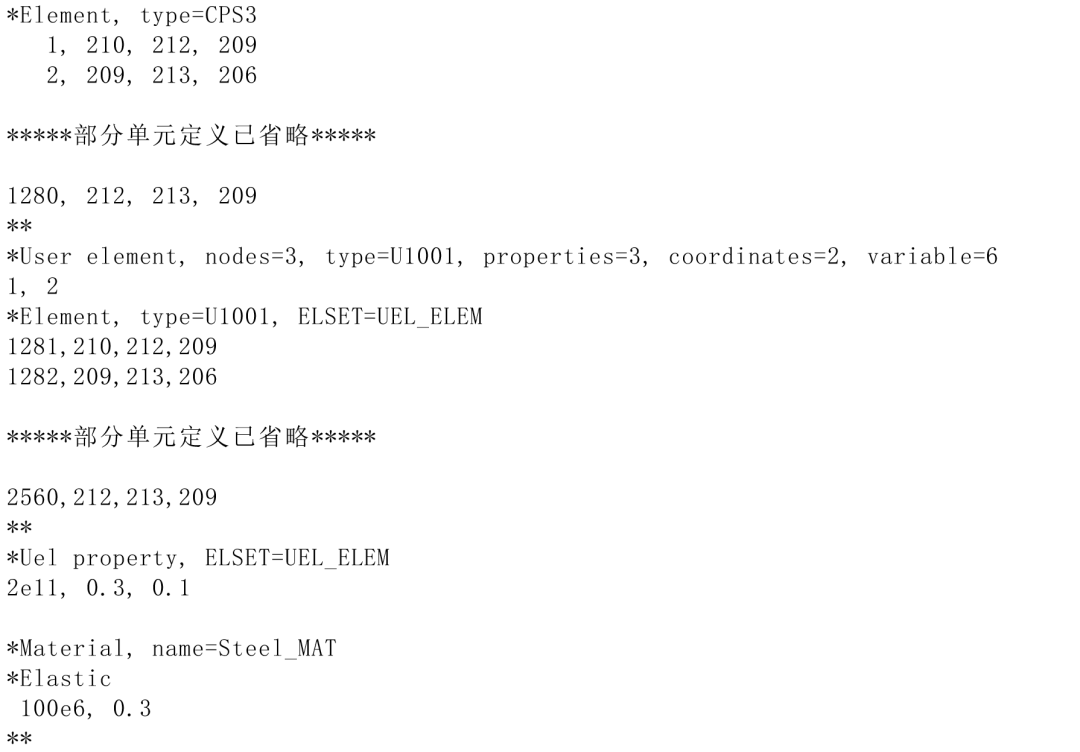 注意,自定义单元和哑单元具有相同的节点号和不同的单元编号。此外,自定义单元和哑单元使用了不同的材料属性,自定义单元为结构本身的材料属性,而哑单元的材料属性本身并没有意义,为了避免对结构的响应产生影响,哑单元的刚度应尽可能的小,出于计算收敛性的考虑,本文将其设定为100MPa。
注意,自定义单元和哑单元具有相同的节点号和不同的单元编号。此外,自定义单元和哑单元使用了不同的材料属性,自定义单元为结构本身的材料属性,而哑单元的材料属性本身并没有意义,为了避免对结构的响应产生影响,哑单元的刚度应尽可能的小,出于计算收敛性的考虑,本文将其设定为100MPa。
基于上述方法,本文分别采用CPS3单元、UEL自定义单元和包覆哑单元的UEL自定义单元对悬臂梁结构进行有限元分析,获得结构的位移分布如图3.2所示。
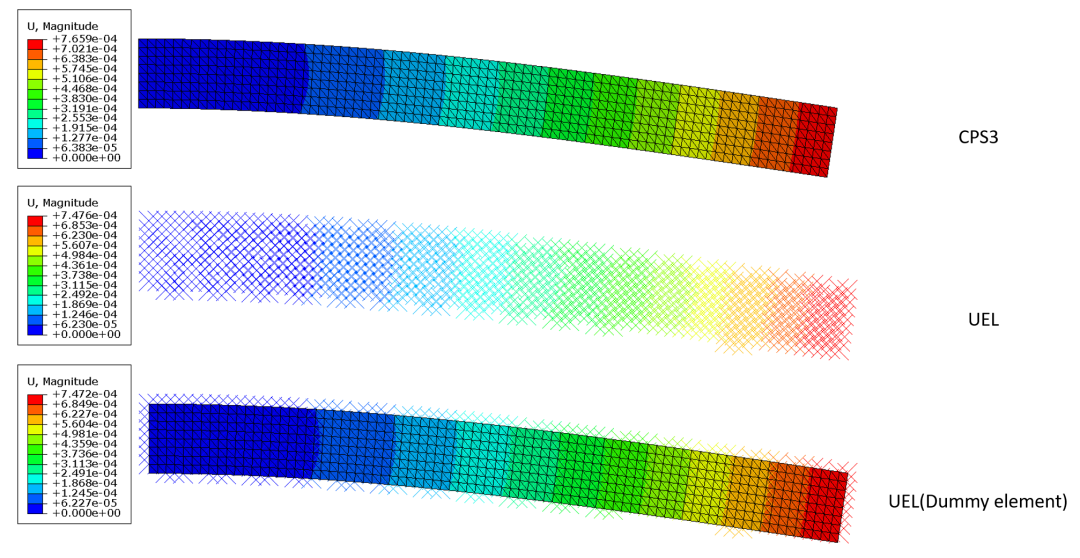
而由经典梁理论可以计算得到悬臂梁的最大挠度为:
可以看到,三种模型计算得到的最大挠度值均小于经典梁理论的挠度值,这是由于3节点三角形平面应力单元过于刚硬,无法较好地反映悬臂梁的弯曲变形模式,因此导致计算结果偏小。这种在一个变形模式或多个变形模型中过于稳定的现象也被称为剪切锁定。Abaqus的CPS3单元似乎针对此类现象对刚度矩阵进行了修正,因此计算结果要略优于自定义单元。而采用哑单元包覆的自定义单元由于引入了额外的刚度值,因此计算得到的挠度值最小。尽管如此,三种模型计算得到的结果都非常接近,如果采用更为细密的网格,预计可以得到更为精确的结果。
后台回复UEL_TRI可获取完整计算模型
附录A: 线性3节点三角形平面应力单元UEL子程序
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 程序用于定义3节点三角形平面应力单元 C
C 单元节点数:3 节点自由度数:2 单元自由度数:2×3=6 C
C 材料参数: (1)弹性模量E (2)泊松比NU (3)单元厚度THICK C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
SUBROUTINE UEL(RHS,AMATRX,SVARS,ENERGY,NDOFEL,NRHS,NSVARS,
1 PROPS,NPROPS,COORDS,MCRD,NNODE,U,DU,V,A,JTYPE,TIME,DTIME,
2 KSTEP,KINC,JELEM,PARAMS,NDLOAD,JDLTYP,ADLMAG,PREDEF,NPREDF,
3 LFLAGS,MLVARX,DDLMAG,MDLOAD,PNEWDT,JPROPS,NJPROP,PERIOD)
C
INCLUDE 'ABA_PARAM.INC'
C
DIMENSION RHS(MLVARX,*),AMATRX(NDOFEL,NDOFEL),PROPS(*),
1 SVARS(*),ENERGY(8),COORDS(MCRD,NNODE),U(NDOFEL),
2 DU(MLVARX,*),V(NDOFEL),A(NDOFEL),TIME(2),PARAMS(*),
3 JDLTYP(MDLOAD,*),ADLMAG(MDLOAD,*),DDLMAG(MDLOAD,*),
4 PREDEF(2,NPREDF,NNODE),LFLAGS(*),JPROPS(*)
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 子程序主要变量说明 C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 需要更新的变量
C
C AMATRX:单元的刚度矩阵 所有非零元素都必须定义
C RHS:单元刚度方程中的右端向量 变量中包含有残余载荷(不平衡力)向量
C SVARS:求解状态变量 状态变量的个数由NSVARS确定(可以不更新)
C ENERGY:用户自定义单元的能量 共有8个分量(可以不更新)
C 传入模型的信息变量(不可修改)
C
C NNODE:自定义单元的节点个数
C JTYPE:单元类型 Un
C NDOFEL:自定义单元的自由度个数
C JELEM:用户指定的自定义单元号
C NSVARS:用户自定义状态变量的个数
C PROPS:单元材料参数实数数组 包含有NPROPS个实数参数
C JPROPS:单元材料参数整数数组 包含有NJPROPS个整数参数
C COORDS:坐标数组 COORDS(K1,K2)为第K2个节点的第K1个坐标
C U:单元计算中的自由度(本单元中为位移)
C DU:位移的增量值
C V:位移对时间的一阶导(Velocity)
C A:位移对时间的二阶导(Acceleration)
C NDLOAD:当前单元激活的分布载荷编号
C MDLOAD:单元中定义的总的分布载荷的个数
C JDLTYP:该整数数组的元素用来标示单元的载荷类型
C ADLMAG:对于一般的非线性分析 ADLMAG(K1,1)为第K1个分布载荷Un在增脸步结束时的大小
C DDLMAG:包含有分布载荷的增量大小 计算外力做功时会用到
C NPREDF:定义的场变量个数
C PREDEF:场变量数组
C NRHS:载荷向量列阵的个数 对于大部分非线性分析 取值为1
C MCRD:节点坐标分量个数与节点自由度个数中的较大值
C LFLAGS:该数组定义有当前分析步的分析类型 以及单元计算所需要进行的内容
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 变量定义及声明 C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C
INTEGER::I,J,K
REAL,PARAMETER::ZERO=0.0
REAL,PARAMETER::ONE=1.0
REAL,PARAMETER::HALF=0.5
REAL::AREA !三角形单元面积
REAL::E !弹性模量
REAL::NU !泊松比
REAL::THICK !单元厚度
C
REAL,DIMENSION(3,1)::DA,DB,DC !构造B矩阵的参数ai bi ci
REAL,DIMENSION(3,3)::D !弹性系数矩阵D
REAL,DIMENSION(3,6)::B !几何函数矩阵B
REAL,DIMENSION(6,3)::B_TRAN !几何函数矩阵B的转置
REAL,DIMENSION(3,6)::S !应力函数矩阵S
REAL,DIMENSION(3,1)::TEMP_U !用于临时存放应变结果
REAL,DIMENSION(3,1)::EPS !用于存放应变结果
REAL,DIMENSION(3,1)::SIGMA !用于存放应力结果
REAL,DIMENSION(6,3)::K_MATRIX !临时存放计算单元刚度矩阵的中间结果
REAL,DIMENSION(6,6)::K_MATRIX2 !临时存放计算单元刚度矩阵的中间结果
REAL,DIMENSION(6,1)::F !用于计算右端矢量RHS
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 基本参数计算 C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 计算构造几何函数矩阵B所需的参数ai bi ci
C 计算中需要用到节点坐标值
C COORDS(K1,K2)表示当前单元第K2个节点上的第K1个坐标
DO K=1,NNODE
I=MOD(K+1,3)
J=MOD(K+2,3)
IF(I.EQ.0)THEN
I=3
ENDIF
IF(J.EQ.0)THEN
J=3
ENDIF
DA(K,1)=COORDS(1,I)*COORDS(2,J)-COORDS(1,J)*COORDS(2,I) !ai
DB(K,1)=COORDS(2,I)-COORDS(2,J) !bi
DC(K,1)=COORDS(1,J)-COORDS(1,I) !ci
ENDDO
C 计算三角形单元面积
AREA=HALF*(DA(1,1)+DA(2,1)+DA(3,1))
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 定义几何函数矩阵 C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 初始化几何函数矩阵B(维度为3×6)
DO I=1,NNODE
DO J=1,NNODE*2
B(I,J)=ZERO
END DO
END DO
C 定义几何函数矩阵B
B(1,1)=DB(1,1)
B(1,3)=DB(2,1)
B(1,5)=DB(3,1)
B(2,2)=DC(1,1)
B(2,4)=DC(2,1)
B(2,6)=DC(3,1)
B(3,1)=DC(1,1)
B(3,2)=DB(1,1)
B(3,3)=DC(2,1)
B(3,4)=DB(2,1)
B(3,5)=DC(3,1)
B(3,6)=DB(3,1)
B=HALF*B/AREA
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 定义弹性系数矩阵 C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 读取材料参数
E=PROPS(1) !弹性模量
NU=PROPS(2) !泊松比
THICK=PROPS(3) !单元厚度
C 初始化弹性系数矩阵D(维度为3×3)
DO I=1,NNODE
DO J=1,NNODE
D(I,J)=ZERO
END DO
END DO
C 定义弹性系数矩阵D
D(1,1)=ONE
D(1,2)=NU
D(2,1)=NU
D(2,2)=ONE
D(3,3)=(ONE-NU)*HALF
D=E/(ONE-NU**2)*D
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 定义应力函数矩阵 C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 定义应力函数矩阵S(维度为3×6)
C 应力函数矩阵S=D・B
CALL MATRIX_MUL(D,B,NNODE,NNODE,NNODE,NNODE*2,S)
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 计算应力和应变 C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 计算应变需要用到节点位移列阵U(维度为6×1)
C 初始化用于存放应变和应力结果的矩阵
DO I=1,3
EPS(I,1)=ZERO
SIGMA(I,1)=ZERO
END DO
C 计算应变结果(维度为3×1)
C EPS=B・U
C 将节点位移列阵U存放到临时变量TEMP_U
DO I=1,NDOFEL
TEMP_U(I,1)=U(I)
END DO
CALL MATRIX_MUL(B,TEMP_U,NNODE,NDOFEL,NDOFEL,1,EPS) !!!!应变计算错误
C 计算应力结果(维度为3×1)
C SIGMA=D・EPS
CALL MATRIX_MUL(D,EPS,NNODE,NNODE,3,1,SIGMA)
C 将应力和应变结果存放至状态变量中
C 共6个状态变量 前3个状态变量存放应变结果 后3个状态变量存放应力结果
DO I=1,3
SVARS(I)=EPS(I,1)
SVARS(I+3)=SIGMA(I,1)
END DO
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 组装单元刚度矩阵和右端向量 C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 注意:UEL子程序组装的是单元刚度矩阵 而非整体刚度矩阵
C 初始化单元刚度矩阵AMATRX和右端向量RHS
DO I=1,NDOFEL
RHS(I,1)=ZERO
DO J=1,NDOFEL
AMATRX(I,J)=ZERO
END DO
END DO
C 计算单元刚度矩阵
C K=B^T・D・B・THICK・AREA
C 计算B矩阵的转置B_TRAN(维度为6×3)
CALL MATRIX_TRAN(B,NNODE,NDOFEL,B_TRAN)
C 计算刚度矩阵AMATRX
CALL MATRIX_MUL(B_TRAN,D,NDOFEL,NNODE,NNODE,NNODE,K_MATRIX) !B^T・D
CALL MATRIX_MUL(K_MATRIX,B,NDOFEL,NNODE,NNODE,NDOFEL,K_MATRIX2) !B^T・D・B
K_MATRIX2=K_MATRIX2*THICK*AREA
AMATRX=K_MATRIX2
C 计算右端矢量
C 计算向量F=B^T・SIGMA(维度为6×1)
CALL MATRIX_MUL(B_TRAN,SIGMA,NDOFEL,NNODE,NNODE,1,F)
F=F*THICK*AREA
DO I=1,NDOFEL
RHS(I,1)=RHS(I,1)-F(I,1)
END DO
RETURN
END
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C 定义计算调用的子程序 C
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
C-------------------------------------------------------------------------
C 矩阵转置子程序
C 子程序名: MATRIX_TRAN
C 功能:B=A^T
C 输入:AMATRIX(矩阵A) AROW(矩阵A行数) ACOL(矩阵列数)
C 输出:CMATRIX(矩阵B)
C-------------------------------------------------------------------------
SUBROUTINE MATRIX_TRAN(AMATRIX,AROW,ACOL,BMATRIX)
C 定义二维数组
INTEGER::AROW,ACOL
REAL,DIMENSION(AROW,ACOL)::AMATRIX
REAL,DIMENSION(ACOL,AROW)::BMATRIX
INTEGER::I,J
C 矩阵转置计算
DO I=1,ACOL
DO J=1,AROW
BMATRIX(I,J)=AMATRIX(J,I)
END DO
END DO
RETURN
END
C-------------------------------------------------------------------------
C-------------------------------------------------------------------------
C 矩阵相乘子程序
C 子程序名: MATRIX_MUL
C 功能:C=AB
C 输入:AMATRIX(矩阵A) BMATRIX(矩阵B) AROW(矩阵A行数) ACOL(矩阵列数)
C BROW(矩阵B行数) BCOL(矩阵B列数)
C 输出:CMATRIX(矩阵C)
C-------------------------------------------------------------------------
C
SUBROUTINE MATRIX_MUL(AMATRIX,BMATRIX,AROW,ACOL,BROW,BCOL,CMATRIX)
C 定义二维实型数组
INTEGER::AROW,ACOL,BROW,BCOL
REAL,DIMENSION(AROW,ACOL)::AMATRIX
REAL,DIMENSION(BROW,BCOL)::BMATRIX
REAL,DIMENSION(AROW,BCOL)::CMATRIX
INTEGER::I,J,K
C 判断矩阵维度是否正确
IF (ACOL.NE.BROW) THEN
WRITE(*,*) 'Matrix size error'
CALL XIT !矩阵维度错误则终止整个分析
END IF
C 计算矩阵乘法
DO I=1,AROW
DO J=1,BCOL
CMATRIX(I,J)=0
DO K=1,ACOL
CMATRIX(I,J)=CMATRIX(I,J)+AMATRIX(I,K)*BMATRIX(K,J)
END DO
END DO
END DO
RETURN
END
C-------------------------------------------------------------------------





