有限元基础编程 | 表面力如何处理？

今日分享的主要内容是：在有限元分析时，我们对于表面力如何处理？

在处理梁单元等效节点载荷是，教材里会给出一些常见的等效节点载荷的形式，直接拿来套用即可。那我们在分析平面模型时，对于分布有表面力，我们是如何处理的呢？

本文从最小势能原理推导出的等效节点载荷公式出发，详细讨论平面单元表面力的处理，并回答之前粉丝咨询的一个问题：为什么均布载荷等效到节点后，两端节点载荷对半折减？

声明：本次分享的内容主要参考了《MATLAB和Abaqus有限元分析理论与应用》和《有限元方法基础教程》，文末均给出商品链接，对有限元感兴趣的小伙伴可着手购买，对有限元的入门学习有很大的帮助。

表面力处理

利用最小势能原理推导出的等效节点载荷如下式所示，第一项为体力，第二项为集中力，第三项为表面力。今天我们只研究第三项的表面力，其余两种情况，日后有机会再介绍。

下图是本次要讲的案例，单元的1-3边分布有均布荷载，我们要做的就是如何将此类型的荷载转化为节点处的荷载。

 

均布载荷作用于单元2-3边上，并与    轴夹角为    ，表面力矢量可表示为    ，上式的面积分可转化为线积分，如下式所示，需要注意的是，在边2-3上，    。

可利用三角形单元边长积分公式：

求得各个节点的等效节点载荷：

两端载荷折减原因

本小节来解释一下为什么多个单元均布载荷节点等效后，出现两端载荷值减半这一现象？

首先我们先考虑1个单元，如下图所示，利用上一节的等效方法，可得等效节点载荷均为    。

 

我们接下来将问题扩展至两个单元，每个单元节点等效后，均会出现    ，故在两个单元共用节点时，载荷值为    ，所以在总体上，我们可以看到两端得载荷值减半的现象。

 

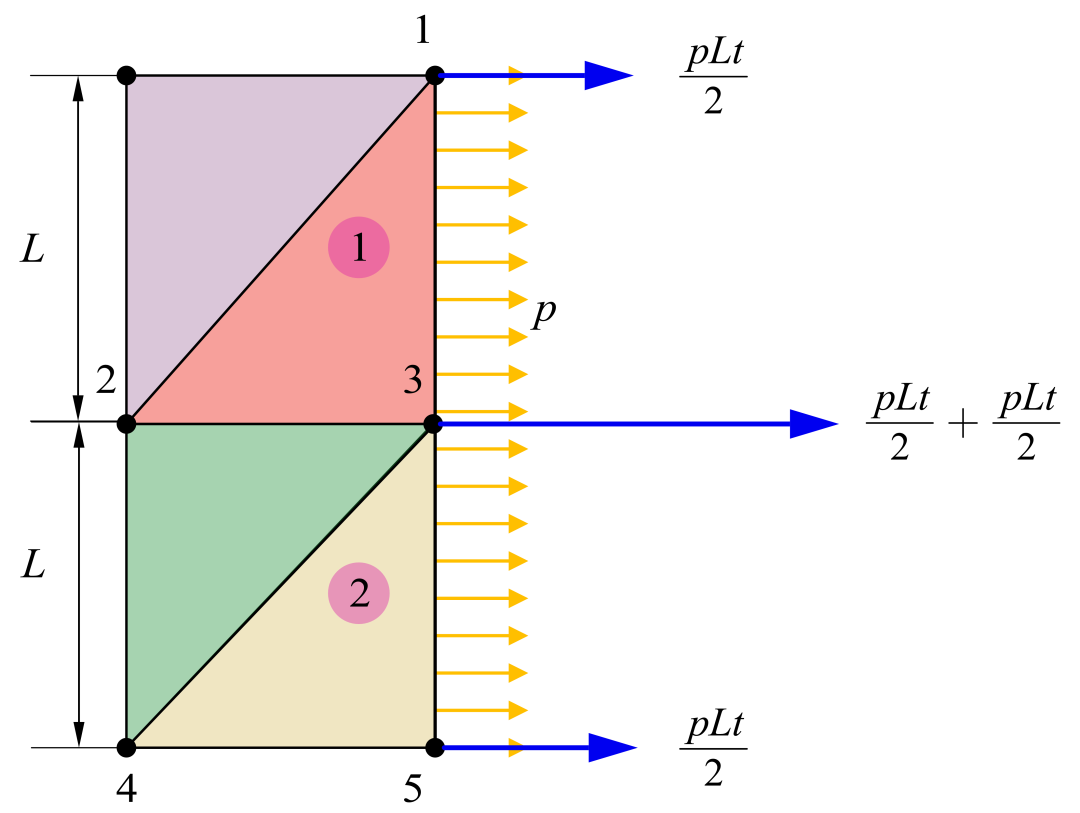
以上解释乃木木一家之言，也是本人看书体会，如有错误，欢迎批评指正，感谢您的阅读。