阻尼类型以及midas NFX、midas MeshFree中的阻尼定义
一、阻尼的分类
粘性阻尼:当物体在流动中运动时发生。阻尼力与速度成正比,因此在动力学分析中要考虑粘性阻尼。比例常数C定义为阻尼常数,常用阻尼比ξ来量化表示。阻尼比ξ是阻尼常数C与临界阻尼Ccr的比值。所谓临界阻尼,就是使得物体不作周期性振动而能最快回到平衡位置。
结构阻尼或者滞后阻尼:是材料的固有特性,是材料内部摩擦产生的阻尼,在动力学分析中应当考虑。
摩擦阻尼:物体在干表面上滑动时产生的阻尼,阻尼力与垂直于表面的压力成正比。动力学分析中一般不考虑。
二、粘性阻尼与结构阻尼的等效关系(以单自由度为例)
粘性阻尼力与速度成正比:
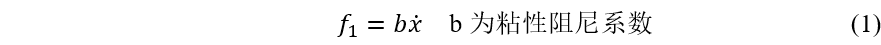
结构阻尼力与位移成比例:
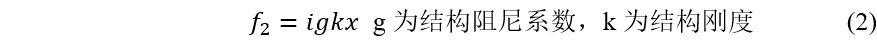
假设结构的简谐响应为:
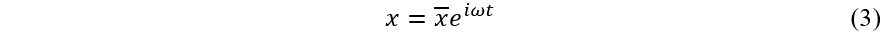
对于粘性阻尼力:
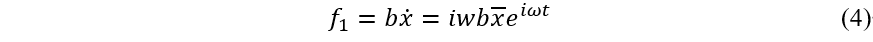
对于结构阻尼力:
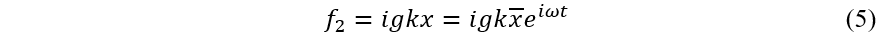
粘性阻尼和结构阻尼等效,可得:

如果:

那么:
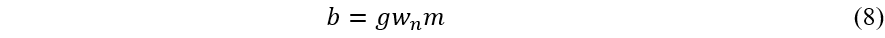
临界阻尼系数:
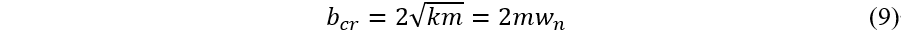
根据阻尼比定义:
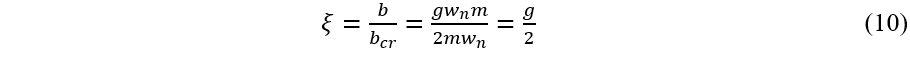
因此在做动力学分析时,结构阻尼一般取阻尼比的2倍。
三、midas NFX中的阻尼功能
对于粘性阻尼的考虑:通过模态阻尼(临界阻尼比、等效粘性阻尼、品质因子)、瑞利阻尼常数α、阻尼单元(Damper)、弹簧-阻尼单元(Bush)定义。
①瑞利阻尼
假定结构的粘性阻尼力正比于质点的运动速度,这时的单元阻尼矩阵为:
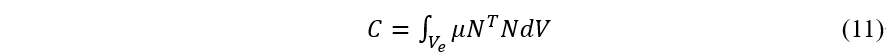
单元阻尼矩阵与单元质量矩阵成比例。
再假定由材料内摩擦引起的结构阻尼比例于应变速率(前面推导粘性阻尼和结构阻尼等效关系时,假设结构阻尼力与位移成比例,注意区别),这时的单元阻尼矩阵为:
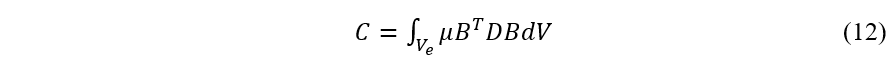
单元阻尼矩阵与单元刚度矩阵成比例。
比例于单元质量矩阵和单元刚度矩阵的阻尼矩阵对于模态振型具有正交性,此时的阻尼矩阵也称为振型阻尼。
式(11)和式(12)中的比例系数,在一般情况下是依赖于频率的,因此在实际分析中,精确地决定阻尼矩阵相当困难。因此,通常将阻尼矩阵简化为质量矩阵和刚度矩阵的线性组合,即

这种振型阻尼称为瑞利阻尼。
midas NFX中瑞利阻尼的定义
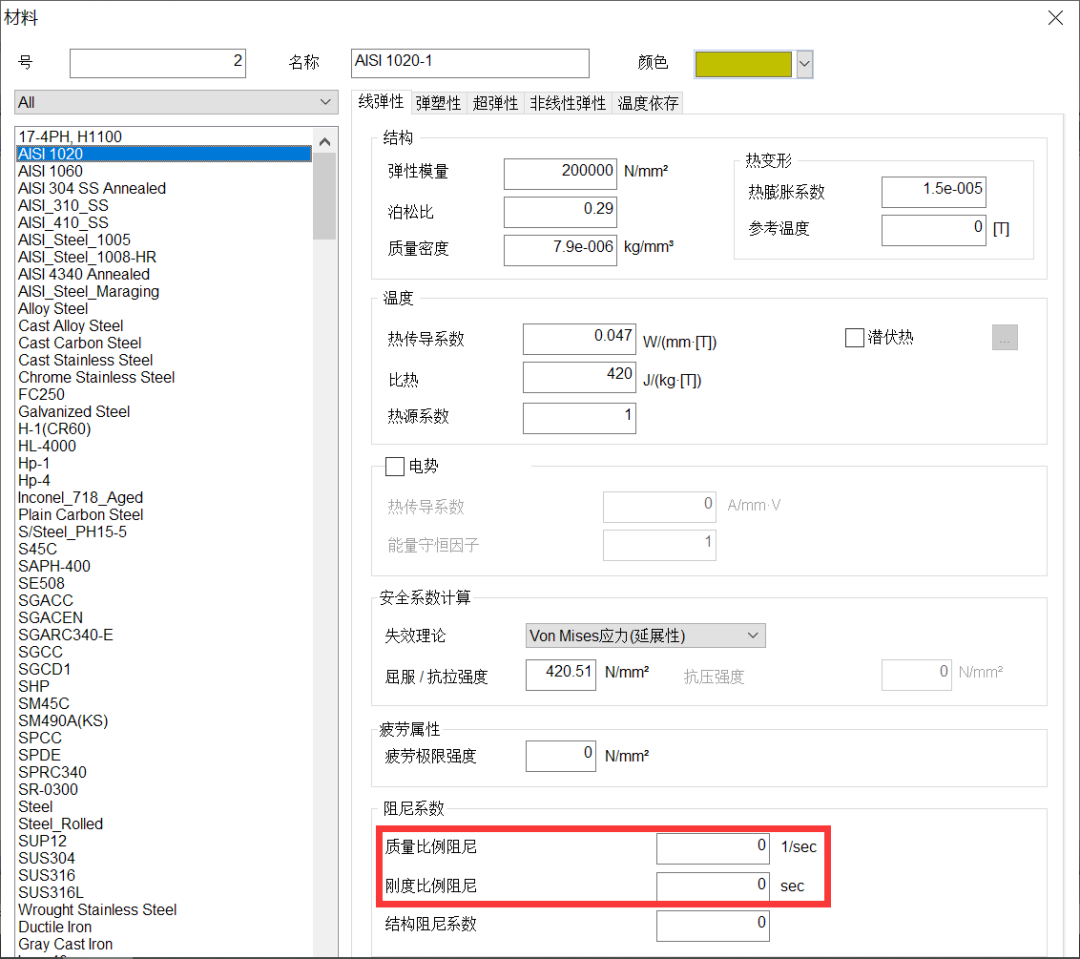
图1 材料定义界面
在midas NFX中,在材料定义窗口,可以输入质量比例常数α和刚度比例常数β。
②模态阻尼
在线性动力分析当中,可以选择用模态法进行求解,模态法中常用的阻尼就是模态阻尼,包含临界阻尼比、等效粘性阻尼以及品质因子。
其中关于临界阻尼比和等效粘性阻尼,见前述。
下面说明品质因子的概念。
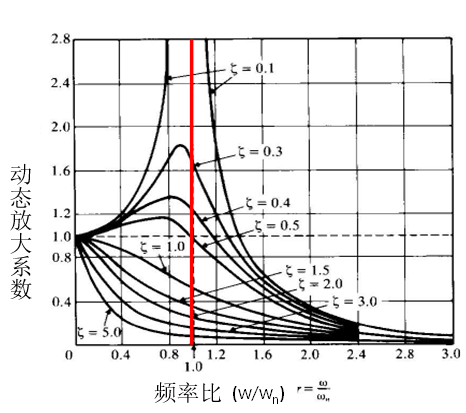
图2 动力放大系数与阻尼比、频率比的关系
动态放大系数是指动力荷载引起的响应幅值与动力荷载幅值作为静荷载所引起的结构静响应之比。动态放大系数与频率比、阻尼比有关,表达式为:

当频率比(荷载频率与固有频率之比)趋向于1时,动态放大系数趋向于1/2ξ。也就是:

A称为品质因子。
midas NFX中模态阻尼的定义
用模态法进行求解时,对系统的动力学方程进行解耦,得到n个单自由度系统的运动方程。
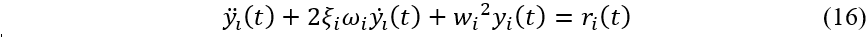
通过模态阻尼定义每个单自由度系统运动方程的阻尼。
在分析控制界面,可定义模态阻尼函数。
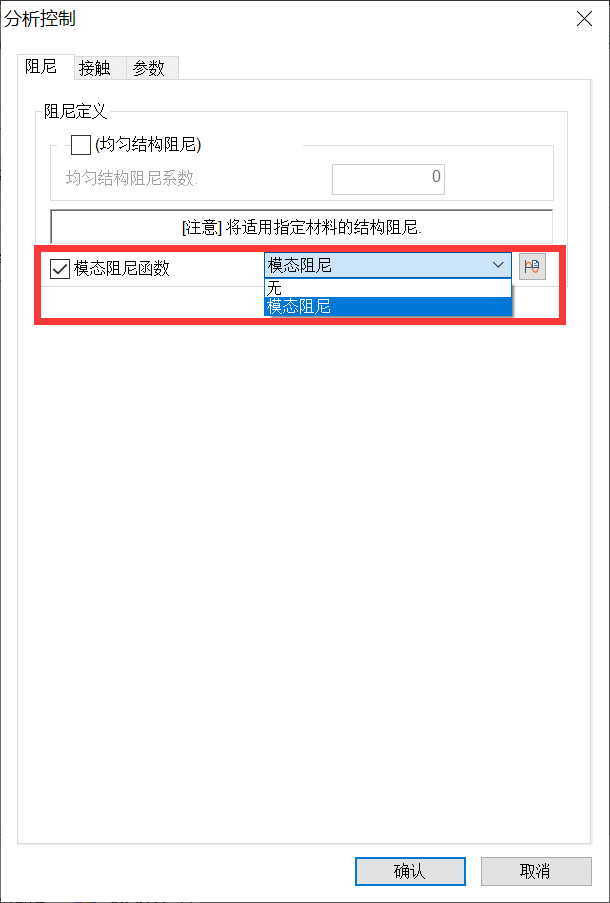
图3 分析控制
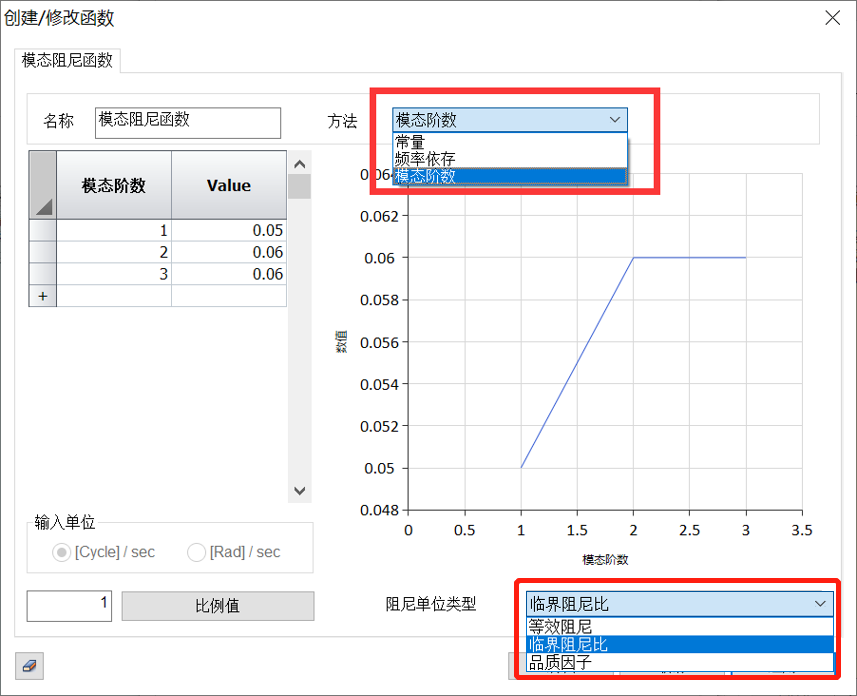
图4 模态阻尼函数定义
从图3中可以看到,模态阻尼定义包含临界阻尼比、等效粘性阻尼和品质因子,定义的方法有常量、频率依存和模态阶数。
常量方法:每个单自由度系统的阻尼都是一样的,是一个常数。
频率依存:输入频率-阻尼函数,根据每个单自由度系统的固有频率计算阻尼。
模态阶数:输入模态阶数-阻尼函数,每个单自由度系统都对应某一阶模态,根据模态阶数计算阻尼。
③指定材料结构阻尼和整体结构阻尼

图5 材料定义界面
在midas NFX中,可以在材料定义界面指定该材料的结构阻尼,结构阻尼的大小一般取阻尼比的2倍。

图6 分析控制界面
在分析控制界面,可以输入整体结构阻尼大小。
在瞬态响应分析中,由于不能考虑复数,所以结构阻尼需要转化为等效粘性阻尼,转化过程可参考第二部分。

其中C是整体阻尼矩阵,K是整体刚度矩阵,Ke是单元刚度矩阵,ge指定的材料结构阻尼,g是整体结构阻尼。w3、w4的取值与荷载的频率一致,如果作用荷载不是周期性动力荷载时可取最小固有频率。
④阻尼单元 (Damper)和弹簧-阻尼单元(Bush)
对于这两种阻尼,将在后续的文章中专门阐述。
四、midas MeshFree中的阻尼功能
对于粘性阻尼的考虑:通过模态阻尼(临界阻尼比、等效粘性阻尼、品质因子)、瑞利阻尼常数α。
对于结构阻尼的考虑:通过瑞利阻尼常数β、整体结构阻尼定义。
其含义、输入界面与midas NFX中的一致,不赘述。
五、总结
1、阻尼可分为三类:粘性阻尼、结构阻尼和摩擦阻尼。摩擦阻尼在动力学分析中一般不考虑。
2、粘性阻尼和结构阻尼的等效关系满足:wb=gk。
3、midas NFX中的阻尼功能:通过模态阻尼(临界阻尼比、等效粘性阻尼、品质因子)、瑞利阻尼常数α、阻尼单元(Damper)、弹簧-阻尼单元(Bush)定义粘性阻尼;通过瑞利阻尼常数β、指定材料结构阻尼、整体结构阻尼定义结构阻尼。
4、midas MeshFree中的阻尼功能:通过模态阻尼(临界阻尼比、等效粘性阻尼、品质因子)、瑞利阻尼常数α定义粘性阻尼;通过瑞利阻尼常数β、整体结构阻尼定义结构阻尼。




