midas NFX|稳定性分析
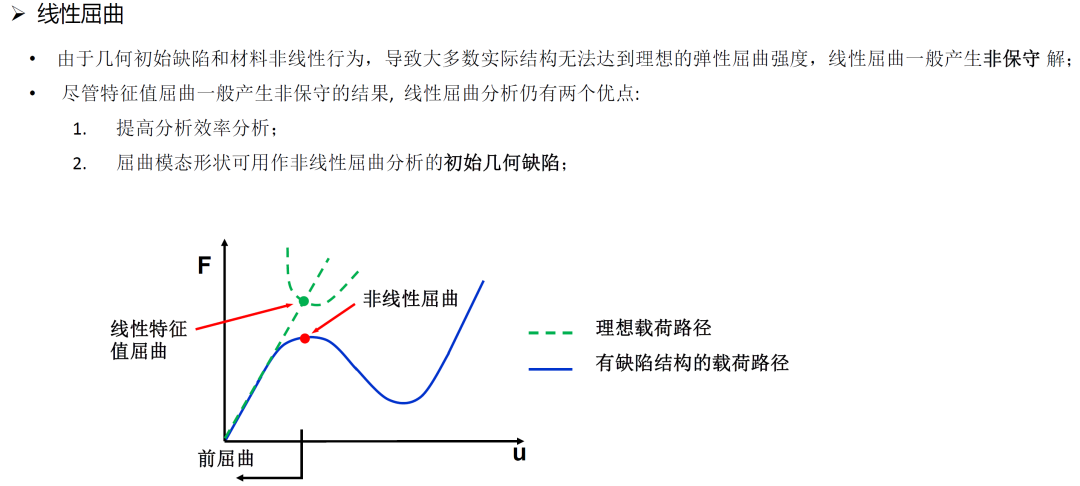
线性屈曲
(一类稳定)
为保证结构的正常工作,其必须满足强度、刚度、稳定性基本的要求,即使强度等性能满足要求,仍然会出现失稳破坏,故稳定性分析是非常重要的内容。稳定性一般可分为局部失稳和整体失稳。如细柱体、压杆和真空罐以及载荷没有实质性变化的情况下,除了一个小的载荷扰动 ), 结构的位移将有一个非常大的变化。


局部失稳:
在钢结构中,受压、受弯、受剪或在复杂应力下的板件由于宽厚比过大,板件发生屈曲的现象。构件发生局部失稳后并不一定立即导致构件的整体失稳,也可能继续维持着构件整体的平衡状态。由于部分板件屈曲后退出工作,使构件的有效截面减小,会加速构件整体失稳而丧失承载能力。

整体失稳:
指随着荷载逐渐增大,结构原始平衡状态转变为不稳定状态。
两种基本形式:
一类稳定
分支点(平衡分叉、质变)失稳
二类稳定
极值点(量变)失稳。

屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷,屈曲分析包括:线性屈曲和非线性屈曲分析。线弹性失稳分析又称特征值屈曲分析;线性屈曲分析可以考虑固定的预载荷,也可使用惯性释放;非线性屈曲分析包括几何非线性失稳分析, 弹塑性失稳分析(材料非线性失稳分析), 非线性后屈曲(Snap-through)分析(包含几何非线性和材料非线性),本文主要以线性屈曲为主。
6月7日稳定分析讲解回顾




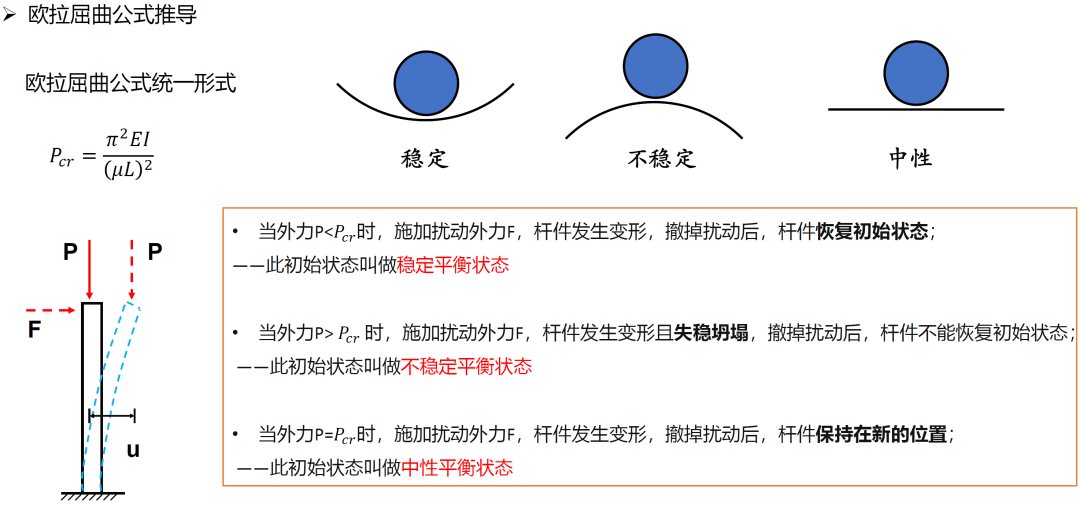


*受压减小刚度,受拉增加刚度,当压力增大到一定数值使刚度减小值等于构件弹性刚度时,构件发生屈曲。


参考资料:
钢结构设计规范 GB 50017-2017
材料力学 (Ⅰ) 第四版 孙训方
结构力学教程Ⅱ 龙驭球 包世华
为什么是钢结构,砼结构没有局部失稳的规定?


简单换算,定性分析:
fs/fcd≈10倍 → 换算为砼截面:tcw/tw=10
→ 砼 h0/tw或b/t≈0.1 钢 h/t或b/t
4.3 受弯构件,钢 h0/tw≤250 → 砼 h0/tw≈25<80
5.4 弯压构件,钢 b/t≤100 → 砼 b/t≈10 <13
注:此处省略√fk/f
分支点失稳




单自由度的分支点失稳

跳跃失稳:
常出现在扁拱或扁桁架结构中,AB是稳定状态,BCD不稳定,B-F出现跳跃,FG又属于稳定平衡,但是,实际工程一般是不允许结构发生跳跃现象的,所以, B点为临界荷载位置。结构的变形在荷载达到临界值前后发生性质上的突变,可视为一种特殊形式的分支点失稳。

极值点失稳:

可见,大位移理论分析的极值点,与初始缺陷ε有关,小位移理论极值与初始缺陷无关;
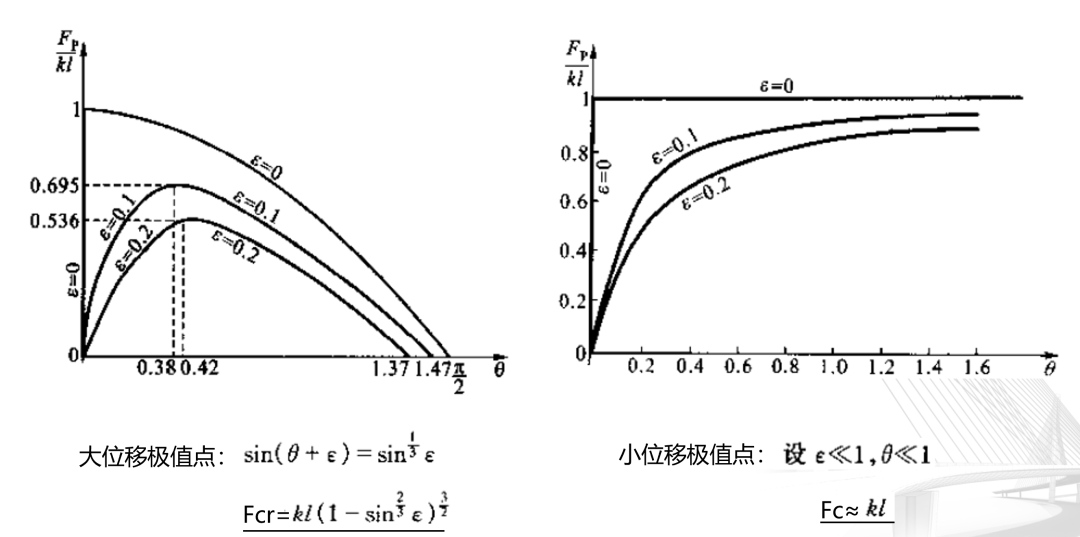
按教材整理

结论:无论完善体系的分支点失稳,还是非完善体系的极值点失稳,都可以用小位移分析和大变形分析理论进行分析。

模态数量:输入需要计算的屈曲模态数量
注:输入值超过结构最大模态数,程序在信息窗口提示,按信息修改一下即可。

特征值出现负值
注:反向加载原因
感兴趣特征值范围:
注:设定特征值输出范围,0-0默认全部输出。
斯图姆(sturm)序列检查
注:检测特征值是否有漏根情况,保证获得使低阶模态的全部特征根。实际工程中,模态较少时,由于收敛判断条件的模糊性,易发生高阶先于低阶收敛的情况,造成丢根。
无限自由度体系的稳定分析公式推导介绍…
略…在无限自由度体系中,平衡方程是微分方程不是代数方程,手算不太现实
现场反馈





