GCKontrol舵机模型的参数调优

2年前浏览1894

Python及GCKontrol API简介

Pythn是一种解释型、面向对象、动态的高级程序设计语言。自从20世纪90年代初Python语言诞生至今，它逐渐被广泛应用于处理系统管理任务和开发Web系统。目前Python已经成为最受欢迎的程序设计语言之一。

由于Python语言的简洁、易读以及可扩展性，众多开源的科学计算软件包都提供了Python的调用接口，例如计算机视觉库OpenCV、三维可视化库VTK、复杂网络分析库igraph等。而Python专用的科学计算扩展库就更多了，例如三个十分经典的科学计算扩展库：NumPy、SciPy和matplotlib，它们分别为Python提供了快速数组处理、数值运算以及绘图功能，因此Python语言及其众多的扩展库所构成的开发环境十分适合工程技术、科研人员处理实验数据、制作图表，甚至开发科学计算应用程序，在人工智能的科学领域也有很多应用。

近年随着数据分析扩展库Pandas、机器学习扩展库scikit-leam以及Python Notebook交互环境的日益成熟，Python也逐渐成为数据分析领域的首选工具。

在GCKontrol中，我们做到了支持Python的API功能，实现了批量仿真和自动化建模、测试的效果。对于建模，GCKontrol API支持自动化创建模型、设置模型参数以及连线；对于仿真，支持打开模型，配置时间信息，运行仿真并获取数据结果。

全局优化与局部优化

2.1 全局优化程序从一系列的初始状态出发，在函数值空间整个区域，最终找到全局稳定点方式是大量的去撒点，大量的去做几何结构优化，然后比较哪一个才是最稳定的。很显然的，这个工作量比较大，很类似挨个尝试的办法。

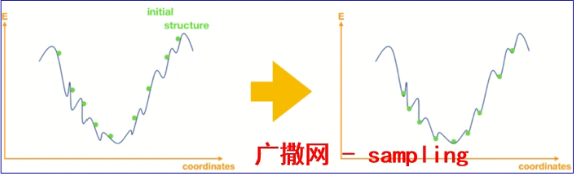
图1 全局优化

2.2 局部优化

无论是量子化学还是密度泛函的计算，与做初始结构是有关的。在初始结构的基础上，构建了初始波函数，或者是初始电子密度，然后进行辩分。当找到某一个局部稳定点位置的时候，它比它周边的所有的点，能量都要低。那么就有一种风险，程序就认为，它不需要再做结构几何优化了，这个地方就是最稳定的。按这个局部的指向，程序又回到这个局部稳定点，这种点叫驻点。

但问题在于，不止一个驻点，局部稳定点有很多个。基于不同的初始结构，它附近的结构稳定点，可能相同，可能不同。程序并没有这个能力，从这样一个局部去识别到全局稳定点。这种情况下并没有得到一个全局稳定点，但这个状态还是稳定的，只是一个亚稳态，结构优化是对初始结构很敏感的，无论是量化计算还是密度泛函的计算都存在这个问题，因此我们往往只能得到，靠近初始点的那个局部稳定点，而不是全局稳定点。

Python与GCKontrol案例：舵机模型

在之前的文章《用GCKontrol搭建电动舵机系统》中，我们介绍了舵机模型的整体架构以及模型的特性，在本文中将继续使用此模型，通过限制优化目标的范围，优化模型的相关参数值，使之仿真结果达到最优。

对于稳定系统，系统动态性能指标通常在系统阶跃响应曲线上来定义。因为系统的单位阶跃响应不仅完整反映了系统的动态特性，而且反映了系统在单位阶跃信号输入下的稳定状态。同时，单位阶跃信号又是一个最简单、最容易实现的信号。

3.1.1最大超调量（简称超调量）

瞬态过程中输出相应的最大值超过稳态值的百分数，即

式中，c_max和c(∞)分别为输出相应的最大值和稳态值，。

3.1.2峰值时间

输出相应超过稳态值第一次达到峰值所需要的时间。

3.1.3上升时间

输出响应第一次达到稳态值的时间。有时也定义为输出从稳态值的10%上升到90%的时间。

图3 动态特性指标

本例中我们重点关注超调量及上升时间两个参数的优化，将限定二者的范围区间，并使仿真结果的误差带始终保持在0.005。

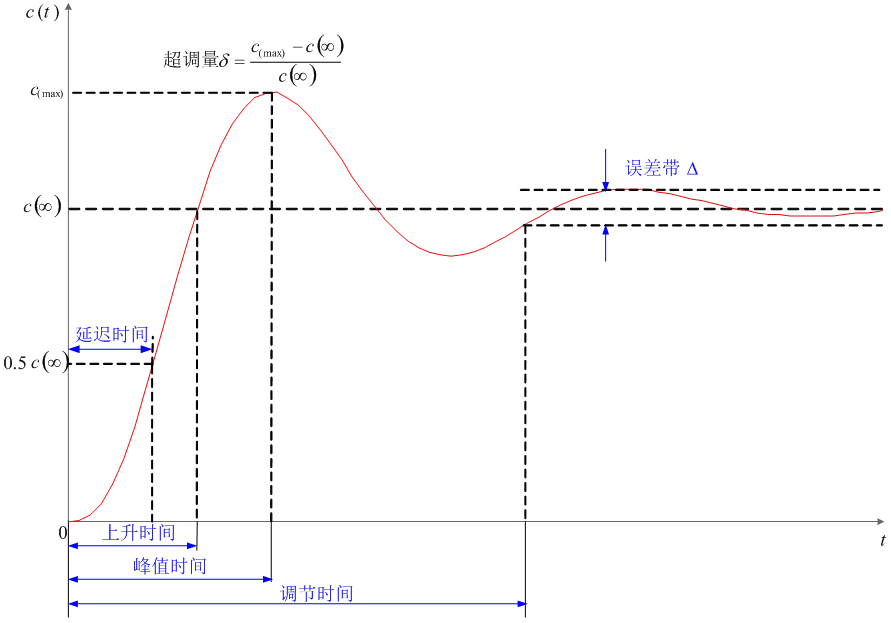
►步骤一：确定参数

根据经验了解到在位置环中Kp_er_rad对舵机的响应速度起主导作用，Ki_er_Rad对舵机的超调起主导作用，所以针对这两个值做组合的运算，找到合理的范围，使响应速度的加快的同时，超调量变小。

图4 Kp与Ki

脚本内容如下：

图5 设置参数的调节范围

►步骤二：确定优化目标

在模型里将目标舵机角度定义为阶跃响应，仿真一次查看目标角度和实际角度的结果曲线如下：

图6 第一次仿真结果图

根据导出的csv数据可知，此次仿真舵机角度最高点的数据为0.039rad，超调量为17.4%，上升时间为0.179s。

接下来我们定义超调量需要在[0,5%]的范围内，上升时间为输出从稳态值的10%上升到90%所需要的时间，这段时间称为响应时间，并且规定响应时间需要在[0,0.05]秒的范围内。脚本内容如下：

图7 响应时间&超调量

►步骤三：获取PID参数设置模块

使用GCKontrol的Python API获取当前正在运行库的名称，并获取所需要的变量值，在这里我们取目标角度、气动力矩和响应角度，并分别命名，如下：

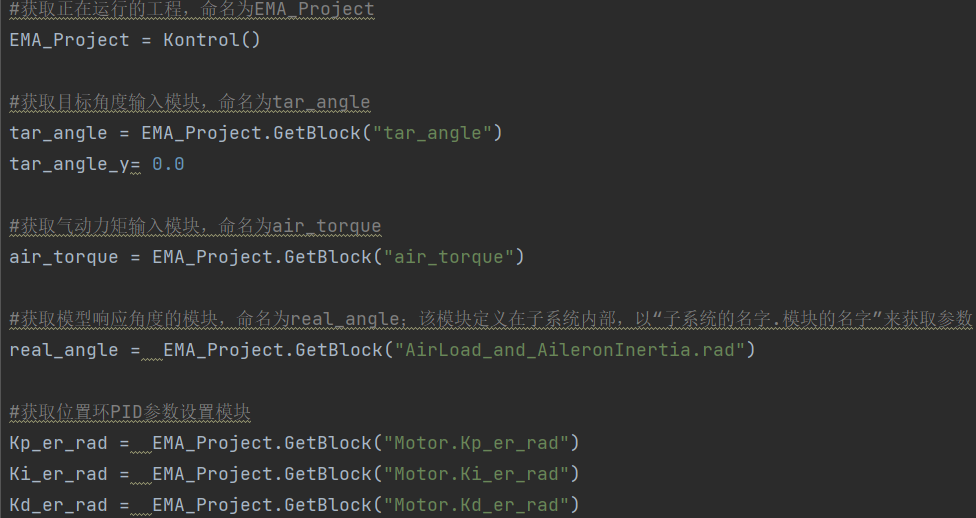
图8 获取PID参数

►步骤四：运行优化

◆PID控制器参数整定方法一：穷举法

穷举法采用排列组合的方式进的循环仿真，根据约束条件计算动态响应时间和超调量：

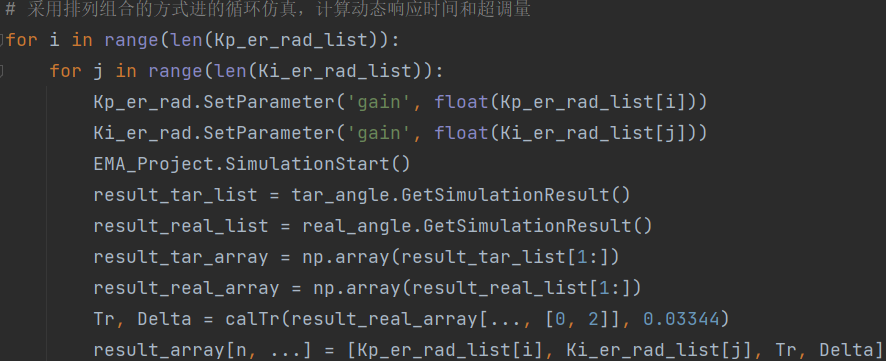
图9 穷举法

约束条件为：超调量必须小于5%并且最终的目标角度值和实际角度值相差小于0.005（rad），并将条件代入到目标方程中。

图10 目标方程

将坐标轴的值换成Kp和Ki实际的值，并画出最终的热力图。

图11 穷举法作图过程

最终运行的结果如下图，可以看出当Kp=105和Ki=137.5处目标方程达到最优（颜色值最深）。

图12 穷举法热力图

方法一是一种“参数空间”扫描的方法，利用穷举法可以找到一个合理的初始参数，继而引入下面的整定方法二：局部优化。

◆PID控制器参数整定方法二：局部优化——minisize

非线性规划是一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。在 python 里用非线性规划求极值，最常用的就是minimize方法，minimize是scipy.optimize中的函数,可以实现非线性规划问题；给定一个优化目标，其可以自动求出优化目标取极值时所对应的参数。

它的使用格式为：scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)。其中部分内容解释如下：

●fun：求最小值的目标函数；

●x0：初始迭代值；

●method：求解的算法，目前可选的有：‘Nelder-Mead’、‘Powell’、‘CG’、‘BFGS’、‘Newton-CG’、‘L-BFGS-B’、‘TNC’、‘COBYLA’、‘SLSQP’等；

●options：其他选项；

■maxiter : 最大迭代次数；

■disp : 是否显示过程信息。

在本示例工程中我们使用Nelder-Mead求解算法， Nelder-Mead 算法是一种求多元函数局部最小值的算法，其优点是不需要函数可导并能较快收敛到局部最小值。对N元函数f(x)（这里把函数自变量用N维矢量来表示），该算法需要提供函数自变量空间中的一个初始点x₁算法从该点出发寻找局部最小值。

将穷举法中获取到的最优值作为初始值，并加入minimize整定方法进行算法求解，内容如下：

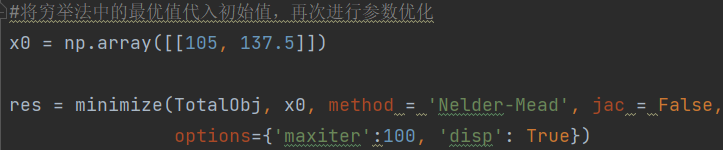
图13 Nelder-Mead

其中，目标方程与图10中的内容一致，初始值x0为（105,137.5），求解算法选择的是Nelder-Mead，由于算法不需要雅克比矩阵，故这里输入False，最大迭代次数为100次，显示过程信息。

在这里我们绘制散点图，并为起始点与终止点在图形中增加注释，由于首次运行不确定终止点的位置，所以在运行第一次的时候，记录了终止点的Kp与Ki的值，并在第二次运行前输入了终止点注释箭头的位置，将图形以最好的方式展示。

图14 minisize法画图过程

图15 散点图

在脚本中将每次仿真的目标方程值打印出来，求得：起始点Kp=105.000，Ki=137.500时，此时的目标方程值为0.267；终止点Kp=115.500，Ki=130.625时，此时的目标方程值为0.263。在GCKontrol的2D面板中可以看出，与图6相比，此次仿真舵机角度最高点的数据为0.035rad，超调量为4.43%，上升时间为0.263s。数据证明不仅降低了超调量和上升时间，并且也能保证每次仿真在合理的范围之内。

图16 minimize法的结果图

非线性化学电子 python 参数优化控制人工智能

著作权归作者所有，欢迎分享，未经许可，不得转载

首次发布时间：2022-09-29