【FCA-Chp-6】第6章 计算微观(细观)力学(1)
在第1章中,假设复合材料的弹性特性可以通过以弹性模量E、剪切模量G、泊松比v等的形式来获得。对于非均质材料,例如复合材料,需要大量材料特性,这些特性的实验测定是一个冗长和昂贵的过程。此外,这些特性的值根据增强材料等的体积分数改变而改变。另一种方法,至少作为实验的补充,是使用均质化技术根据成分(基体和增强材料)的弹性特性预测复合材料弹性特性。因为均质化模型或多或少的基于微观结构的精确建模,这些模型称为微观力学模型,用于得到复合材料特性的近似值的这些技术称为微观力学方法或技术[1]。微观力学模型可用分为经验、半经验、解析和数值模型。精确的半经验模型在文献[1]中描述。
本书仅处理严格的解析或数值模型,不需要经验调整系数,因此不需要实验。因为本书绝大部分针对3D分析,重点放在微观力学模型,可以使用一个模型估计弹性特性的所有参数,而不是使用基于不同假设的不相关的一组模型来组装所需的一组特性。许多均质化的分析技术基于等效本征应变方法[32,33],该方法考虑的是嵌入在一个无限弹性介质中的单个椭圆包含物的问题。文献[34]中使用的Eshelby解发展了一种近似考虑包含物之间相互作用的方法。使用较多的均质化技术之一是自洽法[35],该方法考虑了无限介质中包含物的随机分布。假设无限介质拥有的特性等于要寻找的未知特性。因此,使用一个迭代过程获得全部模量。具有周期性微观结构的复合材料的均质化已通过多种技术完成,包括Eshelby包含物问题[32,33]的延伸、傅里叶级数技术(见6.1.3节和[36,37])、变分原理。周期性本征应变方法进一步发展,可以确定线性粘弹性复合材料的全部松弛模量(见7.6和[38,39])。一个特例,周期性介质的胞元法,考虑一个具有正方形包含物的单位胞元[40]。
目前提到的分析过程可以得到微观力学问题精确解的近似估算。这些估算必须在解的上下限内。有几种变分原理可以用于评估宏观各向同性非均质材料的均质化的弹性特性的界限[41]。这些范围仅依赖于组分的体积分数和物理特性。
为了研究具有周期性微观结构的复合材料的非线性材料行为,使用数值方法,主要是有限元方法。通过观察在指定载荷历程下的微观结构行为,对金属基复合材料的非线性有限元分析进行了研究[42]。复合材料的整体瞬时弹塑性特性的界限已经通过有限元方法推导出[43]。
6.1 解析均质化
如简介中讨论的,非均质介质的平均特性的估计值可以通过各种解析方法得到。方程的详细推导过程超出了本书的范畴。可用的解析模型在负责性和精确性上变化非常大。简单解析模型得到的复合材料刚度C和柔度S张量的公式[40,式2.9和式2.12],如下

式中,Vi、Ci、Si分别为复合材料第i组分的体积分数、刚度和柔度张量(用简化符号)1,I为6×6单位阵。此外,Ai、Bi为第i组分的应变、应力集中张量(用简化符号)[40]。对于纤维增强复合材料,i = f, m分别表示纤维和基体。
1 具有次要对称的四阶张量利用简化符号的6×6矩阵表示。
6.1.1 Reuss模型

2 张量用黑体表示,或用带索引符号的分量表示。
6.1.2 Voigt模型

6.1.3 周期性微观结构模型(Periodic Microstructure Model, PMM)
如果复合材料具有周期性微观结构,或如果可以将其近似为周期性微观结构(见6.1.4节),那么,可以使用傅里叶级数估计复合材料刚度张量的所有分量。纤维增强复合材料的显式公式由[37]推导出,并在下面给出。其中,纤维为各向同性的圆柱形纤维,周期性分布在正方形阵列中(图6.1)。纤维沿x1轴,并且等间距(2a2 = 2a3)。如果纤维在截面内随机分布,则导致复合材料具有横观各向同性特性,如6.1.4节所解释。由横观各向同性纤维增强的复合材料的实例在[39]中介绍,得到的方程在[12]中应用。
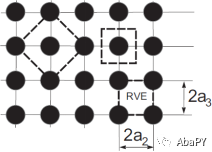
图6.1 周期性正方形纤维阵列复合材料的3种可能的RVE
因为微观结构具有正方形对称性,刚度张量有6个唯一的系数,由下式给出

式中

并且
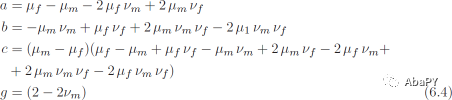
下标()m、()f分别表示基体和纤维。假设纤维和基体都是各向同性的(1.12.5节),两种材料的拉梅常数可以使用式1.75根据弹性模量E、泊松比v和剪切模量G = u而得到。
对于由圆柱形长纤维增强的复合材料,纤维沿x1轴,在正方形阵列中周期性排列(图6.1),a2 = a3,常数S3、S6、S7给出如下[37]
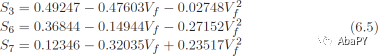
由于微观结构以正方形阵列的形式周期性排列,得到的张量C*具有正方形对称性。因此,张量C*由6个常量描述。然而,大多数复合材料具有随机排列的纤维(见图1.12),导致横观各向同性刚度张量。接下来,横观各向同性材料的概括在6.1.4节介绍。
6.1.4 横观各向同性的平均化
为了得到横观各向同性刚度张量(1.12.4节),在平均意义上相当于具有正方形对称的刚度张量,使用下面的平均化过程。张量C*关于x1轴的转动θ得到





注意,横向剪切模量G23可以用其他工程常数写为以下形式

或者直接使用um、uf如下

式中,D由式6.3给出,a、b、c和g由式6.4给出,S3、S6和S7可以使用式6.5评估。这些等式在PMMIE.m和PMMIE.xls中实现[5]。对于横观各向同性纤维,这些等式在[12]中实现。
例6.1 计算平行圆柱纤维增强复合材料的弹性特性参数,在横截面内形纤维随机分布。成分特性为Ef = 241GPa,vf = 0.2,Em = 3.12GPa,vm = 0.38,纤维体积分数为Vf = 0.4。
解6.1 表6.1中所示的结果使用[12]得到,横观各向同性纤维案例的PMM方程在[12]中实现。
表6.1 单层板弹性特性(Vf = 0.4)

6.2 数值均质化
本节考虑的复合材料具有嵌入在弹性基体中的无限长的圆柱形纤维,如图6.2所示。与纤维轴垂直的复合材料的横截面如图6.3所示,图中清晰展示了周期性微观结构。由于周期性,图6.4中所示的三维代表性体积单元(RVE)可以用于有限元分析。

图6.2 纤维六边形排列的复合材料

图6.3 复合材料横截面

图6.4 代表性体积单元(RVE)
总之,由平行纤维增强的复合材料在中等尺度(单层板水平)表现为正交各向异性材料特性(1.12.3节)。在特殊情况下,例如图6.2和图6.3所示的六边形排列,材料特性变为横观各向同性(1.12.4)。在大多数商业制造的复合材料中,如此精确地控制纤维的布置是不可能的,大多数情况下,产生的微观结构是随机的,如图1.12所示。随机的微观结构导致在中等尺度上的横观各向同性特性。具有随机微观结构的复合材料的分析仍然可以使用假想的周期性微观结构进行,例如图6.1所示的微观结构。然后,如同6.1.4节,平均化刚度张量C以得到横观各向同性材料的刚度张量。更简单的方法是假设随机微观结构可以使用图6.3所示的六边形微观结构很好地近似。这类微观结构的分析直接产生横观各向同性刚度张量,由式1.70表示,为了方便下面再次给出该等式。

式中,1轴沿着纤维方向,上划线表示对RVE体积计算的平均值。一旦知道横观各向同性张量C的元素,均质材料的5个弹性特性参数可以使用式6.11计算得到,即纵向和横向弹性模量E1和E2,纵向和横向泊松比v12和v23,以及纵向剪切模量G12,如下

在横向平面内的剪切模量G23可以使用经典关系(式1.74)或下式直接得到。






对于均质复合材料,平均应力和应变的关系为


通过对施加的应变选择一个单位数值,并且一旦求解由边界条件(式6.13~6.15)定义的问题,则计算应力场σɑ是可能的,其平均值给出了所要求的弹性矩阵的元素,一次得到一列,如下

式中,ɑ, β = 1,...,6(见1.5节)。积分(式6.18)使用Gauss-Legendre求积法在每个单元内评估。商用程序,例如Abaqus,具有逐个单元计算平均应力和体积的能力。因此,积分(式6.18)的计算很容易。更多细节见例6.2。
在矩阵C中的系数通过对式6.10中的每一列设置不同的问题求解得到,如下。
1)矩阵C的第一列
为了确定元素Ci1(i = 1, 2, 3),施加下面的应变在纤维方向(x1方向)拉伸RVE

因此,图6.4中的RVE的位移边界条件(式6.13~6.15)变为

式6.20中的边界条件约束了RVE对面的相对位移。因为RVE的对称性和边界条件(式6.20)的对称性,只需要对RVE的1/8建立有限元模型。假设对上-右-前部分建模(图6.5),可以使用下面的等效外部边界条件,即,位移和应力分量上的边界条件。


图6.5 RVE的1/8模型(注意,模型中纤维沿z轴方向,相当于等式中的x1方向)
上面这些边界条件非常容易施加。对称边界条件施加在x1 = 0、x2 = 0、x3 = 0平面上。然后,均匀位移施加在平面上x1 = a1。在基于位移的公式化中,不需要明确地施加应力边界条件。在式6.21中,位移分量代表应变,沿x1方向位移不为0,沿其他两个方向位移为0。式6.21中列出的应力边界条件反映了这样的事实:在使用的坐标系下,复合材料是宏观正交各向异性的,并且组分材料也是正交各向异性的。因此,在拉伸和剪切应变之间没有耦合。这由式6.10中第4~6列对角线上方的0系数证明。
式6.10中第1列的系数使用式6.18可得,如下
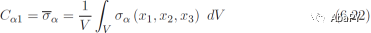
2)矩阵C的第2列
元素Cα2(α = 1, 2, 3)通过以下设置来确定

因此,可以使用下面的位移边界条件
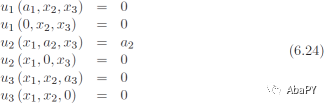
应力边界条件不重要,此处不再列出,因为基于位移的有限元分析公式会自动施加应力。使用式6.18,矩阵C的第2列的刚度计算如下

3)矩阵C的第3列
由于材料的横观各向同性(式6.10),矩阵C第3列的元素可以从第1、2列 确定,所以不需要进一步计算。然而,如果需要,元素Cα3(α = 1, 2, 3)可以通过施加下面的应变而得到。

因此,可以使用下面的位移边界条件
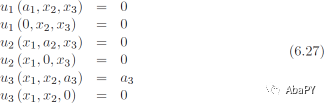
矩阵C的要求的元素通过平均应力场来确定,如同式6.18。
例6.2 计算单向复合材料的E1、E2、v12和v23,其中各向同性纤维Ef = 241GPa、vf = 0.2,各向同性基体Em = 3.12GPa、vm = 0.38,纤维体积分数Vf = 0.4。纤维直径为df = 7um,六边形阵列分布,如图6.3所示。
解6.2 如图6.4所示,根据六边形阵列的微观结构,选择RVE的a2、a3尺寸使Vf = 0.4。RVE的纤维体积和总体积为

两者之比为体积分数。因此,

此外,根据六边形阵列模式,确定a2和a3之间的关系如下

这两个关系可以得到a2和a3,而a1尺寸可以任意选取。本例中,RVE的尺寸为


i. 设置工作路径
菜单:File,Set Work Directory,[C:\SIMULIA\user\Ex_6.2]
菜单:File,Save As,[C:\SIMULIA\user\Ex_6.2\Ex_6.2.cae]
ii. 创建部件
# 下面使用的数值替换相应的变量。
# 数值单位为微米
# a_1 = 1.3175 # 沿x_1方向(拉伸方向)的一半RVE
# a_2 = 5.270 # 沿x_2方向的一半RVE
# a_3 = 9.138 # 沿x_3方向的一半RVE
# r_f = 3.5 # 纤维半径
模块:Part
菜单:Part,Create,3D,Deformable,Solid,Extrusion,Cont
菜单:Add,Line,Rectangle,[0,0],[a_2, a_3],X,Done,Depth [a_1],OK
菜单:Tools,Partition
Cell,Sketch planar partition,Sketch Origin:Specify
# 选取:前面(z=a_1),Sketch origin X, Y, Z:[0, 0, a_1]
Select an (原文and,应为an)edge:vertical and on the right,# 选取:右侧竖直边
菜单:Add,Circle
[0,0],[0,r_f]
[a_2,a_3],[8.77,a_3],X,Done
Extrude/Sweep,# 选取:形成下方1/4圆的线,Done
Extrude Along Direction,# 选取平行于全局Z轴的边,OK
Create Partition
# 选取:上侧实体(较大实体),Done
# 选取:形成上侧1/4圆的线,Done
Extrude Along Direction,# 选取平行于全局Z轴的边,OK
Create Partition,Done,# 关闭Create Partition对话框
iii. 定义材料、截面,并赋截面给部件
模块:Property
菜单:Material,Create
Name [Fiber],Mechanical,Elasticity,Elastic,Type:Isotropic
[241000, 0.2],OK
菜单:Material,Create
Name [Matrix],Mechanical,Elasticity,Elastic,Type:Isotropic
[3120, 0.38],OK
菜单:Section,Create
Name [Fiber],Solid,Homogeneous,Cont,Material:Fiber,OK
菜单:Section,Create
Name [Matrix],Solid,Homogeneous,Cont,Material:Matrix,OK
菜单:Assign,Section
# 选取:基体,Done,Section:Matrix,OK
# 选取:两个纤维,Done,Section:Fiber,OK,Done
iv. 创建装配
模块:Assembly
菜单:Instance,Create,Independent,OK
v. 定义分析步。需要3个分析步,每个对应6.2节中的一列。为了求解本例,需要在Output Requests中设置输出场边量S和IVOL。
模块:Step
菜单:Step,Manager
Create,Name [Column-1],Insert new step after:Initial
Procedure type:Linear perturbation,Static,Cont,OK
Create,Name [Column-2],Insert new step after:Column-1
Procedure type:Linear perturbation,Static,Cont,OK
Create,Name [Column-3],Insert new step after:Column-2
Procedure type:Linear perturbation,Static,Cont,OK
# 关闭Step Manager对话框
环境栏Step:Column-1
菜单:Output,Field Output Requests,Edit,F-Output-1
Edit variables,[S, E, U, IVOL],OK
vi. 添加载荷和边界条件
边界条件在3个载荷分析步中定义,分别用于得到第1、2、3列的系数Cαβ。每次沿每个方向施加一个单位应变。式6.18用于得到刚度系数。过程如下。
模块:Load
# 每个分析步各有一组边界条件
# 对于分析步:Column-1
菜单:BC,Manager
Create,Name [xsymm-C1],Step:Column-1,Mechanical,Symm/Anti/Enca,Cont
# 选取:x=0和x=a_2的面,Done,XSYMM,OK
Create,Name [ysymm-C1],Step:Column-1,Mechanical,Symm/Anti/Enca,Cont
# 选取:y=0和y=a_3的面,Done,YSYMM,OK
Create,Name [zsymm-C1],Step:Column-1,Mechanical,Symm/Anti/Enca,Cont
# 选取:z=0的面,Done,ZSYMM,OK,# 注意只选取一个面
# 施加位移(单位应变)
Create,Name [disp-C1],Step:Column-1,Mech.,Disp/Rota,Cont
# 选取:z=a_1的面,Done,# 勾选:U3 [a_1],OK
# 对于分析步:Column-2
Create,Name [zsymm-C2],Step:Column-2,Mechanical,Symm/Anti/Enca,Cont
# 选取:z=0和z=a_1的面,Done,ZSYMM,OK
Create,Name [ysymm-C2],Step:Column-2,Mechanical,Symm/Anti/Enca,Cont
# 选取:y=0和y=a_3的面,Done,YSYMM,OK
Create,Name [xsymm-C2],Step:Column-2,Mechanical,Symm/Anti/Enca,Cont
# 选取:x=0的面,Done,XSYMM,OK,# 注意只选取一个面
# 施加位移(单位应变)
Create,Name [disp-C2],Step:Column-2,Mech.,Disp/Rota,Cont
# 选取:x=a_2的面,Done,# 勾选:U1 [a_2],OK
# 对于分析步:Column-3
Create,Name [xsymm-C3],Step:Column-3,Mechanical,Symm/Anti/Enca,Cont
# 选取:x=0和x=a_2的面,Done,XSYMM,OK
Create,Name [zsymm-C3],Step:Column-3,Mechanical,Symm/Anti/Enca,Cont
# 选取:z=0和z=a_1的面,Done,ZSYMM,OK
Create,Name [ysymm-C3],Step:Column-3,Mechanical,Symm/Anti/Enca,Cont
# 选取:y=0的面,Done,YSYMM,OK,# 注意只选取一个面
# 施加位移(单位应变)
Create,Name [disp-C3],Step:Column-3,Mech.,Disp/Rota,Cont
# 选取:y=a_3的面,Done,# 勾选:U2 [a_3],OK
# 关闭BC Manager对话框
vii. 对模型划分网格
模块:Mesh
菜单:Seed,Instance,Approximate global size [0.5],OK
菜单:Mesh,Controls,# 选择所有实体,Done
Element Shape:Hex,Technique:Structured,OK
菜单:Mesh,Element Type,# 选择所有实体,Done
Geometric Order:Linear,# 勾选:Reduced integration,OK
菜单:Mesh,Instance,Yes
viii. 求解并可视化结果
模块:Job
菜单:Job,Manager
Create,Cont,OK,Submit,# 当完成后,Results
系数Cαβ和层压板弹性常数使用下面给出的Python脚本计算,该脚本可以输入或粘贴到Python shell中。另外,也可以通过Abaqus/CAE的菜单→File→Run Script来运行Python脚本。脚本srecover.py可从[5]获取,并在本例中使用该脚本。现在,单击Abaqus/CAE底部的>>>从信息窗口切换到命令行窗口(Python shell)。然后,输入或复 制下面的Python程序到Python shell。
# srecover.py
from visualization import *
# 为当前Job打开输出数据库
odb = openOdb(path=’Job-1.odb’);
myAssembly = odb.rootAssembly;
#
# 为frame数据创建一个临时变量
# 提供相同功能,提高处理速度
# Column-1
frameRepository = odb.steps[’Column-1’].frames;
frameS=[];
frameIVOL=[];
# 仅获取最后一个frame [-1]
frameS.insert(0,frameRepository[-1].fieldOutputs[’S’].getSubset(
position=INTEGRATION_POINT));
frameIVOL.insert(0,frameRepository[-1].fieldOutputs[’IVOL’].getSubset(
position=INTEGRATION_POINT));
# 总体积
Tot_Vol=0;
# 应力和
Tot_Stress=0;
#
for II in range(0,len(frameS[-1].values)):
Tot_Vol=Tot_Vol frameIVOL[0].values[II].data;
Tot_Stress=Tot_Stress frameS[0].values[II].data * frameIVOL[0].values[II].data;
# 计算平均值
Avg_Stress = Tot_Stress/Tot_Vol;
print ’Abaqus/Standard Stress Tensor Order:’
# 根据Abaqus Analysis User’s Manual - 1.2.2 Conventions -
# Convention used for stress and strain components
print ’Average stresses Global CSYS:11-22-33-12-13-23’;
print Avg_Stress;
C11 = Avg_Stress[2] # z分量,1方向
C21 = Avg_Stress[0] # x分量,2方向
C31 = Avg_Stress[1] # y分量,3方向(见图6.5)
# Column-2
frameRepository = odb.steps[’Column-2’].frames;
frameS=[];
frameIVOL=[];
# 仅获取最后一个frame [-1]
frameS.insert(0,frameRepository[-1].fieldOutputs[’S’].getSubset(
position=INTEGRATION_POINT));
frameIVOL.insert(0,frameRepository[-1].fieldOutputs[’IVOL’].getSubset(
position=INTEGRATION_POINT));
# 总体积
Tot_Vol=0;
# 应力和
Tot_Stress=0;
#
for II in range(0,len(frameS[-1].values)):
Tot_Vol=Tot_Vol frameIVOL[0].values[II].data;
Tot_Stress=Tot_Stress frameS[0].values[II].data * frameIVOL[0].values[II].data;
# 计算平均值
Avg_Stress = Tot_Stress/Tot_Vol;
print ’Abaqus/Standard Stress Tensor Order:’
print ’Average stresses Global CSYS:11-22-33-12-13-23’;
print Avg_Stress;
C12 = Avg_Stress[2] # z分量,1方向
C22 = Avg_Stress[0] # x分量,2方向
C32 = Avg_Stress[1] # y分量,3方向(见图6.5)
# Column-3
frameRepository = odb.steps[’Column-3’].frames;
frameS=[];
frameIVOL=[];
# 仅获取最后一个frame [-1]
frameS.insert(0,frameRepository[-1].fieldOutputs[’S’].getSubset(
position=INTEGRATION_POINT));
frameIVOL.insert(0,frameRepository[-1].fieldOutputs[’IVOL’].getSubset(
position=INTEGRATION_POINT));
# 总体积
Tot_Vol=0;
# 应力和
Tot_Stress=0;
#
for II in range(0,len(frameS[-1].values)):
Tot_Vol=Tot_Vol frameIVOL[0].values[II].data;
Tot_Stress=Tot_Stress frameS[0].values[II].data * frameIVOL[0].values[II].data;
# 计算平均值
Avg_Stress = Tot_Stress/Tot_Vol;
print ’Abaqus/Standard Stress Tensor Order:’
print ’Average stresses in Global CSYS:11-22-33-12-13-23’;
print Avg_Stress;
C13 = Avg_Stress[2] # z分量,1方向
C23 = Avg_Stress[0] # x分量,2方向
C33 = Avg_Stress[1] # y分量,3方向(见图6.5)
#
EL=C11-2*C12*C21/(C22 C23) # 长度方向模量E1
nuL=C12/(C22 C23) # 12泊松系数
ET=(C11*(C22 C23)-2*C12*C12)*(C22-C23)/(C11*C22-C12*C21) # E2
nuT=(C11*C23-C12*C21)/(C11*C22-C12*C21) # 23泊松系数
GT=(C22-C23)/2 # 或 GT=ET/2/(1 nuT) # 23剪切刚度
#
print "If Moduli are in TPa and dimensions in microns, results are in TPa"
print "E1=",EL
print "E2=",ET
print "PR12=",nuL
print "PR23=",nuT
# end srecover.py
结果在表6.2中给出。如果运行报错,检查for循环后面的空白行是否完全空的。需要用这些空白行作为Python中for循环的终止符。另外,尝试直接运行脚本,菜单:File→Run Script:[srecover.py]→OK。
表6.2 计算得到的单向板的弹性特性参数

(*)本例中使用的边界条件不可能得到
例6.2的建模过程比较复杂。如果希望进行参数化研究,在CAE图形用户界面(GUI)中用交互式方法重新进行建模过程则相当费时和容易出错。但是,可以获取在交互式操作过程中CAE生成的Python脚本,并使用该脚本自动完成建模过程。
4)矩阵C的第4列
对于横观各向同性材料,根据式6.10,在第4列中预期只有C44不等于0,并且可以使用其他元素确定,所以不需要进一步计算。因此,它可以由下式确定。

如何材料是正交各向异性,则必须使用与计算第6列相同的过程。
5)矩阵C的第5列
对于横观各向同性材料,根据式6.10,在第5列中只有C55不等于0,而且等于C66,可以从第6列中得到C66。如果材料是正交各向异性,则必须使用与计算第6列相同的过程。
6)矩阵C的第6列
由于没有载荷的对称性,在这种情况下,采用与前3列类似的方法,使用边界条件是不可能的。因此,边界条件的施加必须使用耦合约束方程(constraint equations,在多数商用有限元分析软件中称为CE)。
根据式6.10,只有C66不等于0。元素Cα6通过以下设置确定。




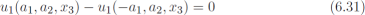



作为推论,在RVE的边和顶点的约束方程必须从式6.30中分离出来单独写。此外,在一对边或一对顶点之间可以仅写3个方程(每个位移分量ui一个方程)。简言之,只有3个位移可以用于实施周期性条件。



添加式6.31和式6.33得到一个方程如下
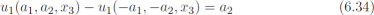
对u2和u3分量重复该过程,使用式6.34将得到的方程分组,得到

在图6.6中边B和D之间考虑式6.30,得到


图6.6 RVE的顶视图,展示两个位移(竖直和水平)必须
施加在边上以产生剪应变(如点A、B、C、D所示)
由面x1 = ±a1和x3 = ±a3定义的两对边,被下列6个约束方程约束。

由面x2 = ±a2和x3 = ±a3定义的两对边的6个约束方程为

注意,式6.35-6.38没有应用在顶点,因为关于RVE体心对称的每对顶点之间会出现冗余约束方程。因此,对于4对顶点,需要一次约束一对。产生的约束方程如下
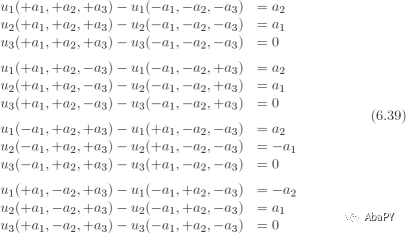
方程(式6.30-6.39)使用式6.39给定的单位应变对RVE的体积施加约束。该模型的有限元分析得到应力的所有分量。如前面讨论的,这些应力分量逐个单元的平均可以从有限元分析得到(见例6.1中的宏srecover),或者应力分量的平均值可以通过简单的后处理计算得到。因此,对于本例,使用式6.18得到的系数C66可以写为如下形式。

最后,复合材料的弹性特性使用式6.11确定。
例6.3 计算例6.2中的复合材料的G12。


纤维直径是df=7um,RVE的尺寸为:

几何(模块:Part)、材料和截面(模块:Property)、装配(模块:Assembly)、分析步(模块:Step)和网格(模块:Mesh)可以用例6.2中使用的方法创建。

模块:Load
菜单:BC,Manager
Create,Name [ysupp],Step:Step-1,Mechanical,Disp/Rota,Cont
# 选取y=-a_3处的面,Done,# 勾选:U2 [0]和U3 [0],OK
Create,Name [ydisp],Step:Step-1,Mechanical,Disp/Rota,Cont
# 选取y=a_3处的面,Done,# 勾选:U3 [18.276] # 2*a_3,OK
Create,Name [xsymm],Step:Step-1,Mechanical,Symm/Anti/Enca,Cont
# 选取x=-a_2和x=a_2处的面,Done,XSYMM,OK
# 关闭BC Manager对话框

在Interaction模块中应用Tie约束,如下。
模块:Interaction
菜单:Constraint,Create
Type:Tie,Cont
Choose the master type:Surface
# 选取前面(z=2*a_1处的面),Done
Choose the slave type:Surface
# 选取后面(z=0处的面),Done
Position Tolerance:Specify distance:[2.635] # 2*a_1
# 不勾选:Adjust slave surface initial position
# 不勾选:Tie rotational DOF if applicable
定义两面之间的距离(位置公差)非常重要,以便CAE可以找到两个面上的节点。
用户可以从.rec文件中提取上面伪代码对应的Python脚本。求解本例的完整的脚本在[5,Ex_6.3-TC.py]得到。脚本可以在Abaqus/CAE中运行,通过菜单:File,Run script:Ex_3.11.cae6.3-TC.py运行。它包含[5,srecover.py],用于计算平均应变和平均应力,并由此可得表6.3中所示的结果。
表6.3 单向板的面内剪切模量


图6.7 例6.3中应变E23的变形和云图(注意坐标系X、Y、Z)





