用Wolfram语言破解球面像差光学问题

破解一个2000年之久的古老谜团
破解一个2000年之久的光学谜团并非易事。然而,蒙特雷科技大学(译注:学校简称ITESM或TEC,是拉丁美洲规模最大的私立大学之一,也是墨西哥最著名的私立大学)博士生Rafael G. González-Acuña却瞄准了这样一个问题:解决镜片中的球面像差问题。考虑到不同方向的折射,光线如何聚焦在一个点上?这个问题在两千年前希腊数学家戴克里克斯(Diocles)的作品“燃烧的镜子”(On Burning Mirrors)中就已经产生。而克里斯蒂安·惠更斯(Christiaan Huygens)在1690年曾坦言,即使是艾萨克·牛顿(Isaac Newton)和戈特弗里德·莱布尼兹 (Gottfried Leibniz)也无法理清头绪。
但今天,González-Acuña和他的同事决定使用Wolfram语言及其计算工具来面对这个古老的问题。结果呢?一个突破性的文章最近横空出世,通过精度为99.999999999%的模拟光束,解释了镜头图像的中心为什么(如何)比在边缘处更清晰。
很巧的是,González-Acuña参加了Wolfram暑期学校,我们有幸采访到他并详细了解他的工作。
Q: 您是如何想到用Wolfram语言解决光学问题的?
A: 我对光学研究的兴趣在我攻读物理学士学位时就开始了,我对成像问题很感兴趣。
当我正在为手动解决代数问题而困扰时,我的同事Héctor A. Chaparro-Romo告诉我,Mathematica非常擅长代数操作和计算。
幸运的是,蒙特雷科技大学有Mathematica的站点许可证,所以我很快就开始使用并且喜欢上了Mathematica。它显示结果的方式,运算内联的方式,以及默认情况下进行代数计算的方式都很令我喜欢。
Q: 你试图解决的问题是什么?
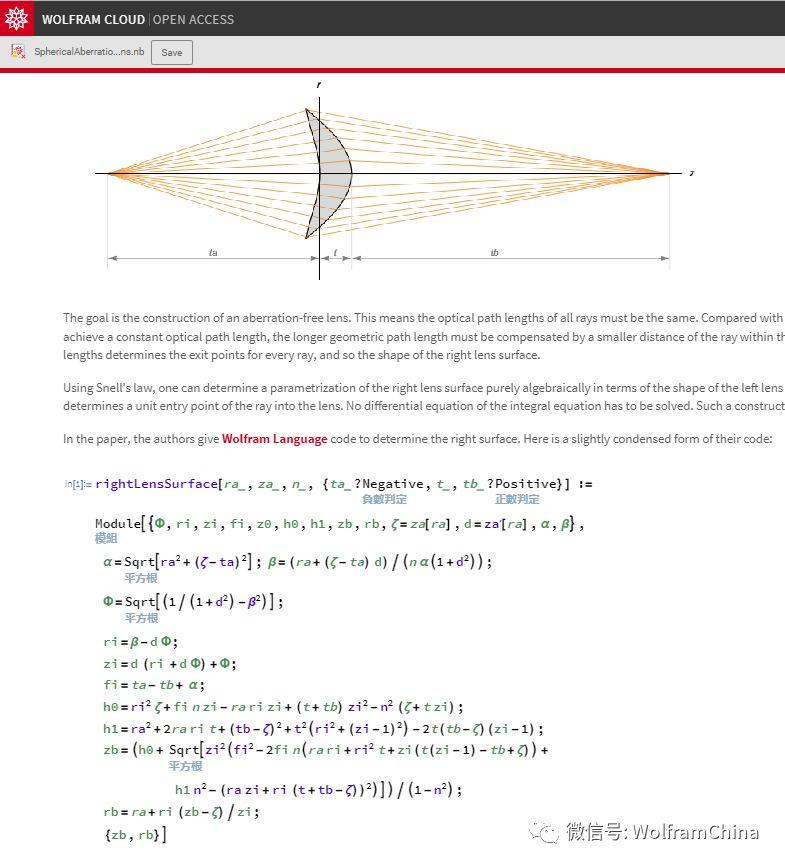
A: 我想要解决的问题是球面无像差镜头的设计。换句话说,从一个物点发出的所有光束穿过镜头会聚在一个像点中。这个古老的问题在两千年内没有解析解,主要是因为其冗长的代数表达式,我的意思是,一个一般方程本身就超过11页!
这个问题有许多数值解,但数值解和解析解之间的差异是无法估量的– 解析解保留了问题的物理特性。我不仅找到了问题的通解,而且还发现解是唯一的,Mathematica是一个很好的工具。
我的研究结果相继以“General Formula for Bi-aspheric Singlet Lens Design Free of Spherical Aberration” (https://doi.org/10.1364/AO.57.009341) 和“General Formula to Design a Freeform Singlet Free of SphericalAberration and Astigmatism”(https://doi.org/10.1364/AO.58.001010)为题,发表在权威杂志《应用光学》中。

上图为透镜中球面像差问题的方程
Q: 你以前和现在都是如何开发解决方案的?
A: 我花了好几个月时间研究这个问题。这是一种痴迷。我一直与我的共同作者Chaparro-Romo交流 - 我们是一个团队,分享代码、想法和可能的解决方案;为了解决自由形式镜头的问题,我们有过很多次非常棒的讨论。
我读过几篇与牛顿有关的对该问题的评论。事实上,克里斯蒂安·惠更斯(Christiaan Huygens)在他的著作《光之论》(Treatise on Light)中提到牛顿、莱布尼兹和笛卡尔都未能成功给出解决方案。

而实际上,惠更斯在他的《光之论》第六章得到了一个近似的解决方案:
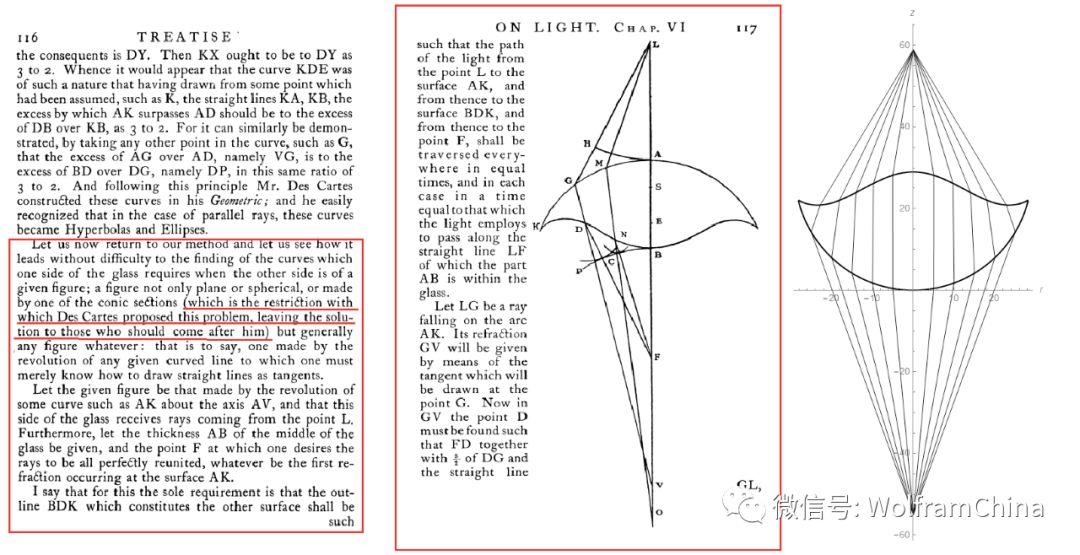
Christiaan Huygens的1690年著作《光之论》摘录,以及Rafael的Mathematica笔记本输出(最右)
但是经过这么多年,我们现在已经得到了300多年前由惠更斯、笛卡尔、莱布尼兹和牛顿以及2000多年前的戴克里斯所寻求的方程式。查看我们的Wolfram笔记本关于构建无球差镜头的简介,了解Rafael G. González-Acuña和 Héctor A. Chaparro-Romo的解决方案:
https://develop.open.wolframcloud.com/objects/exploration/SphericalAberrationFreeLens.nb