如何采用simulink求解常微分方程组

通常来说，求解一个系统的话采用常微分方程组去做。前面也有采用scipy进行了常微分方程组的求解简单介绍，当然需要用到Python。其实完全可以不用任何代码，只用一些simulink模块以搭积木的形式完成这个过程，而且还会方便很多。下面就介绍一下相关的方法。

所用到的核心模块其实就是integrate模块，只需要启动matlab打开simulink然后脱出一个该模块就可以了。

首先以如下方程为例，假设初始值为0，求解区间为【0-10】

采用如下的方式搭建

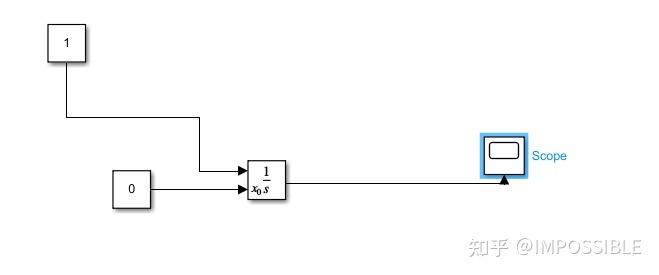simulink中的模块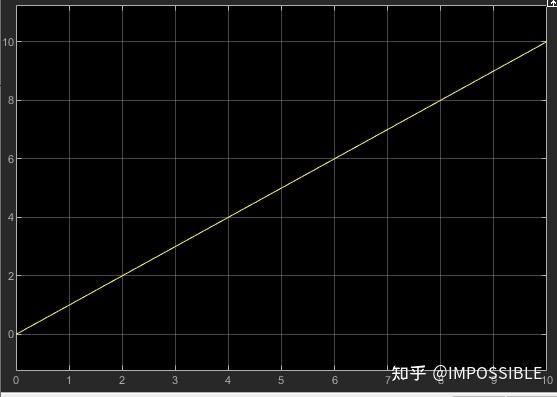求解的结果

当然这个有点简单，来一个稍微复杂一点的

计算过程的模块搭建如下

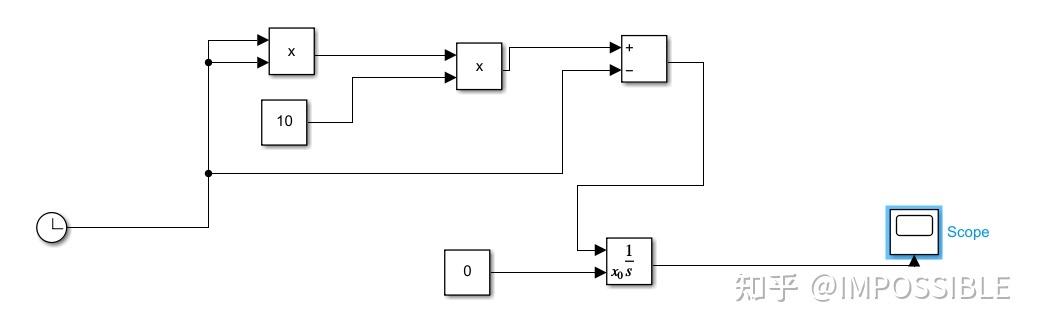simulink中的模块

计算结果如下

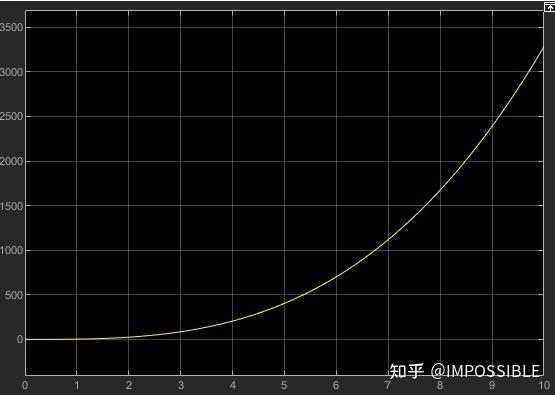simulink中求解结果

当然完全完全可以求解更加复杂的问题，比如以下面的一个方程组为例

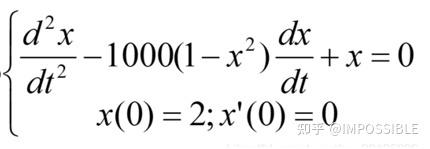
那么他的搭建模块如下所示

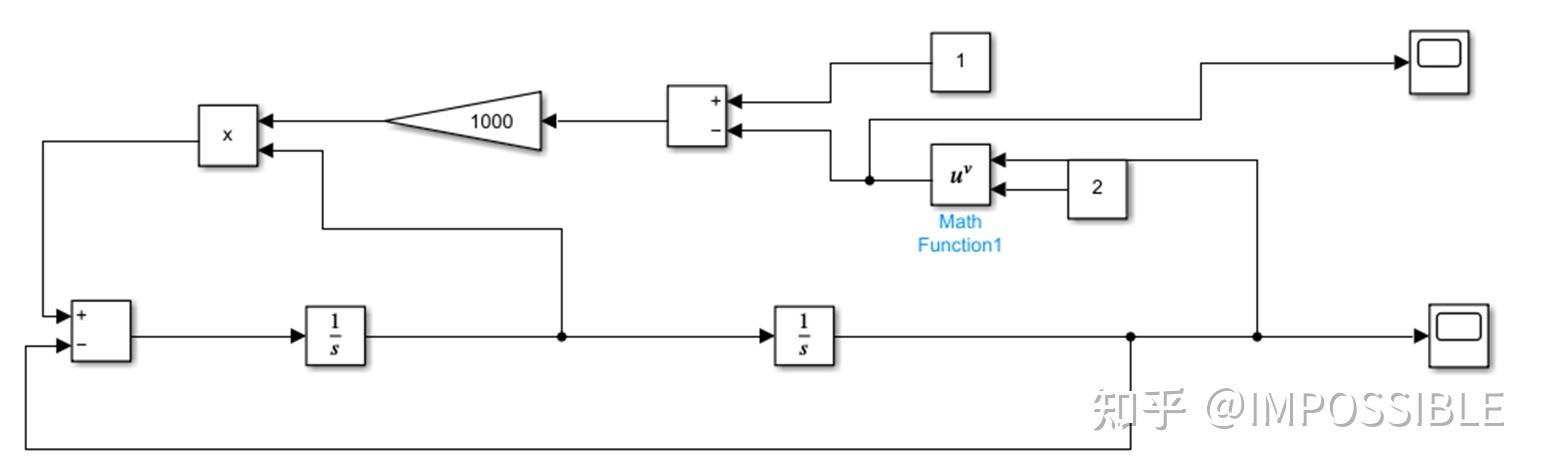
方程组越大，则模块会越复杂，一般可以把一部分单独拿出来做一些封装，然后把这个作为自己的模块老使用，作为演示，我这里也有一个例子，就是pemfc燃料电池的例子，方程组的关系如下。

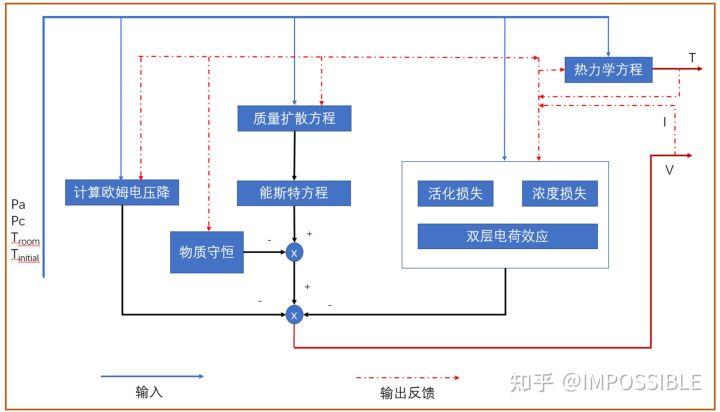pemfc的系统所用到的方程

那么对应的模块搭建如下，可见对于较大的模型搭建还是比较难得

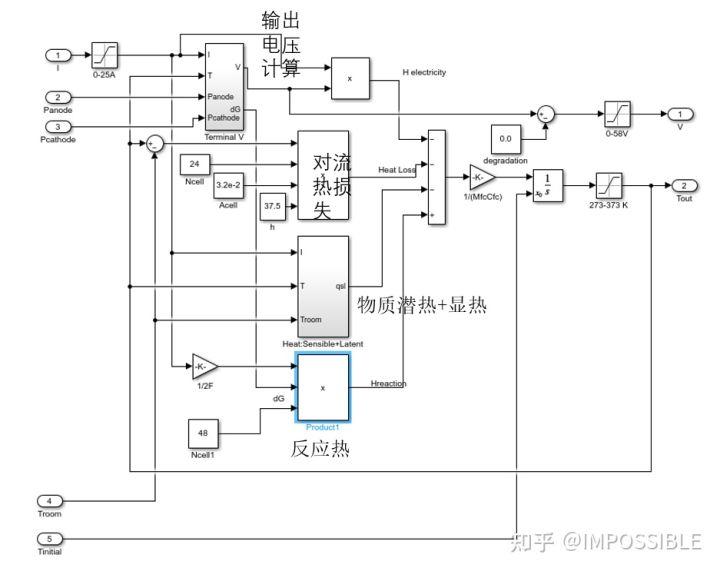
作为对比，我也用做了一个相同功能的模块，下面是一些电池电压计算过程，完整的代码后续上传。

from 能斯特电压 import ecellfrom 单电池电压损失 import conc,act1,act2,ohmicfrom scipy.integrate import solve_ivpdef voltage(I,T,Panode,Pcathode,eps = 0.001):
    ecel = (ecell(I,T,Panode,Pcathode))[0]
    conc_ = conc(T,I)
    act1_ = act1(T)
    act2_ = act2(I,T)
    ohmic_ = ohmic(I,T)

    v1 = conc_/(eps I) (act2_/(eps I))
    v1 = max(0.00001,v1)
    v1 = min(10, v1) #3.24写到这里


    def fun(t,vc):
        dydt = (I   0.01 - vc / v1) / 4
        return dydt

    sol = solve_ivp(fun, (0, 1), [0], method='Radau')
    vc = sol.y.reshape(-1)
    print(ohmic_)

    VOL = (ecel - vc[-1]-act1_-ohmic_)*48
    VOL = max(0,VOL)
    VOL= min(58, VOL) #3.24写到这里

    return VOL,(ecell(I,T,Panode,Pcathode))[1]# if __name__ == "__main___":vol = voltage(25, 345.13,1, 1, eps=0.001)print(vol)

可见两者实现这些功能的方法是大同小异的。