一款工作于S-Band的腔体同轴梳状滤波器设计
一款工作于S-Band的腔体同轴
梳状滤波器设计
Stone 2022年2月
微波腔体滤波器广泛运用于电子对抗和无线通信等领域中,它因具有低损耗、高Q值、远寄生通带、可承受高功率等特点而备受青睐。完全从零基础开始学习滤波器基础理论并仿真得出一款腔体滤波器电气性能曲线,在没有指导的情况下,需要走不少的弯路。鉴于此,依据自身的学习经历写这篇文章,给腔体滤波器初学者提供一个方法和思路,希望基于此可以使初学者掌握一款腔体滤波器分析方法及仿真流程。
1、梳状腔体滤波器原理
梳状腔体带通滤波器是由一系列耦合金属谐振柱组成的。谐振柱是由一端接地,另一端通过加载电容的金属柱体所构成。滤波器的输入和输出是由金属线与谐振柱连接构成,如图1所示:
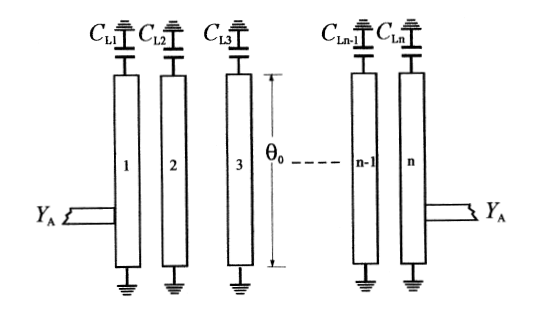
图1 梳状腔体滤波器结构
本文3-D EM全仿真模型采用矩形空气腔包裹谐振柱,谐振柱采用圆柱形状内部预留一定深度可以使调谐螺钉深入,如图2所示:
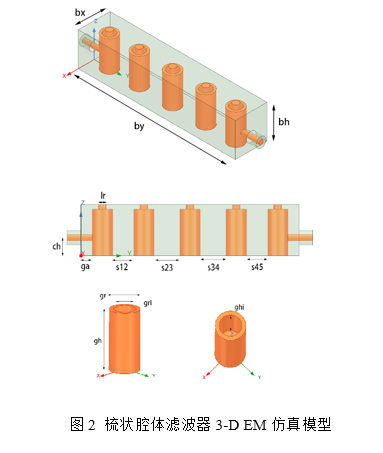
2、梳状腔体滤波器设计指标
本文所要设计的梳状滤波器技术指标为:
-Center Frequency(中心工作频率): 2.8GHz
-Bandwidth(工作带宽):252MHz
-Rejection(带外抑制): >35dB@2500MHz and 3100MHz
-Impedance(阻抗): 50 ohms
3、腔体滤波器设计步骤
1)依据指标计算出滤波器阶数、Q值、耦合系数时延:利用滤波器基础理论或者couplefila等软件,依据指标确定滤波器的阶数、零点位置和拓扑结构,最终计算得出耦合系数与时延。
2)依据中心频率与Q值仿真出单个谐振器尺寸。
3)依据耦合系数,扫描对应耦合结构尺寸。
4)依据外部Q值或者时延,设计输入输出结构。
5)建立整体仿真模型。
6)调试与优化。
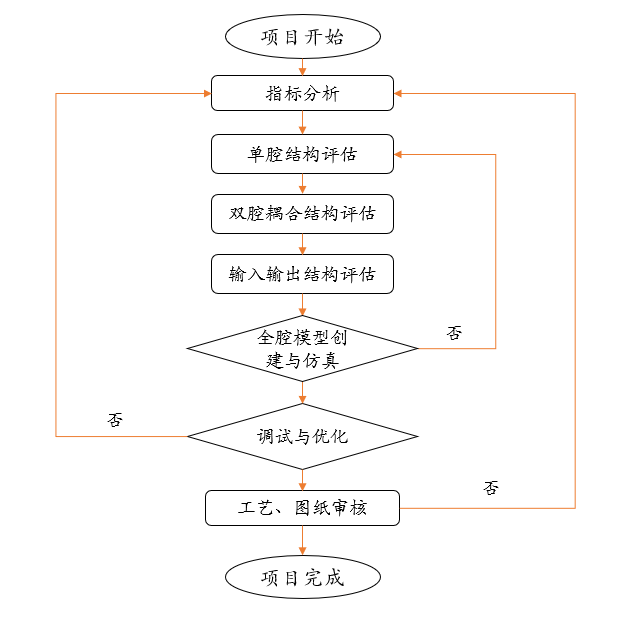
图3 腔体滤波器设计流程
从腔体滤波器的整体仿真流程中可以看出,整体项目中总共引入了三次判断。第一次发生在全腔模型的创建与仿真,这一步主要检验前面综合过程得到的尺寸参数用于全腔建模时,模型是否存在错误或者需要修改的地方。第二次是全腔模型的调试和优化,以判断当前模型是否能优化出满足指标的电气曲线。第三次就是最终的工艺与图纸审核,判断是否满足加工要求。
4、详细分析与设计过程
4.1 依据指标计算出滤波器阶数、Q值、耦合系数和时延
4.1.1 滤波器阶数计算
依据滤波器技术指标,采用切比雪夫低通原型滤波器响应,利用如下公式(1)来计算滤波器的阶数n:
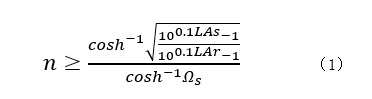
式中,式中𝐿𝐴𝑟表示纹波,可以用回波损耗LR来表示如公式(2):
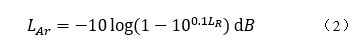
Las表示带外抑制要求,𝛺𝑠表示归一化频率,用公式(3)来计算得到:

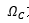 为切比雪夫低通原型滤波器响应中的截止频率,因此等于1,FBW为带通滤波器相对带宽比
为切比雪夫低通原型滤波器响应中的截止频率,因此等于1,FBW为带通滤波器相对带宽比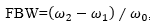 , 𝜔0为带通滤波器中心角频率, 𝜔1 和 𝜔2实际带通滤波器上下边频截止频率。
, 𝜔0为带通滤波器中心角频率, 𝜔1 和 𝜔2实际带通滤波器上下边频截止频率。
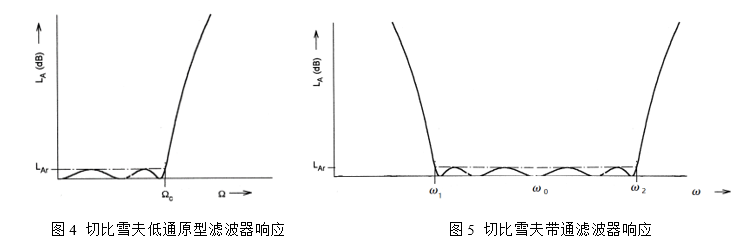
因此若当前所设计的这款中心工作频率为2.8GHz的滤波器的回波损耗为-20dB,代入公式计算得到n≥4.8,取整数阶数就为n=5。
第二种方法计算阶数就是利用目前市面上的相关软件如Couplefila或者CST里面集成的CST Filter Designer 3D(需要使用CST2019版本以上),这两者是同一个东西。利用软件就无需采用公式就能计算得到阶数、耦合系数等相关信息。打开CoupleFila如图6所示,在指标窗口中输入滤波器中心频率2800,带宽252,Q值设置为2000(当前设计没有插入损耗要求,因此暂定按2000的Q来设计),然后在设置阶数为5阶时,可以看到如图7所示的滤波器响应曲线,在响应曲线中设置带外抑制2500和3100查看当前设置是否满足带外抑制-35dB要求。
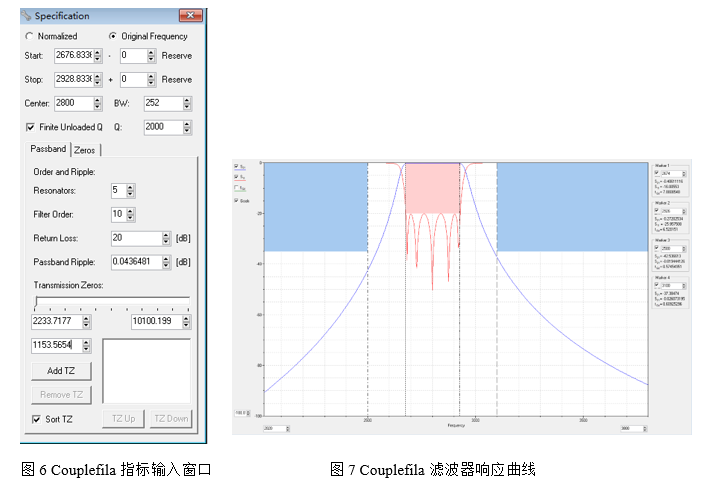
Couplefila相当比前面介绍的公式计算方法,由于可以观察当前所设计滤波器的响应曲线,因此更能直观的反映当前所设计的滤波器情况。
4.1.2 Q值的确定
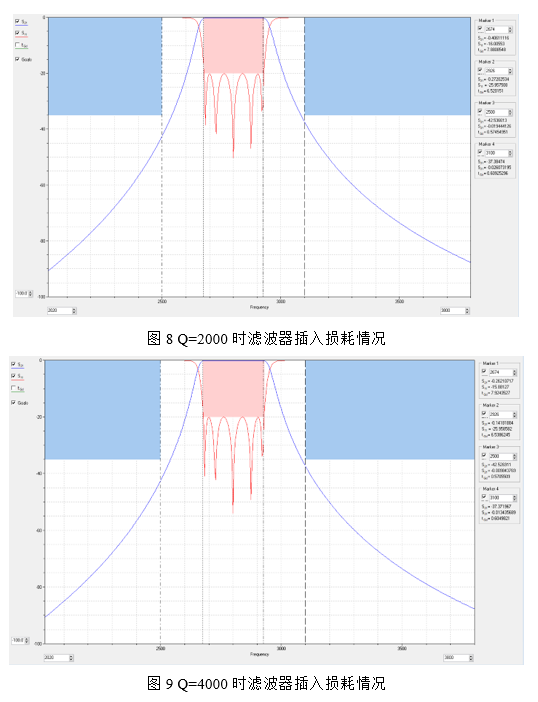
当前所设计腔体滤波器指标,由于只是一个简单的演示,因此并没有在指标要求中提出插入损耗的要求。插入损耗的影响因素有Q值、阶数和带外抑制,主要影响因素为Q值。可以在Couplefila中保持阶数与带宽恒定,改变Q值大小查看对插入损耗的影响,通常Q值越高,插入损耗越好。如果Q=2000时,可以看到当前滤波器工作频带2674-2926MHz插入损耗最差为-0.406dB。
4.1.3 耦合系数与时延计算
采用切比雪夫低通原型响应5阶并且回波损耗为-20dB情况下,计算得到的低通原型滤波器电路的参数如下表1所示:

低通原型参数的计算方法有查表法和公式法,这里介绍公式法,采用的公式如下:

当计算得到低通原型初值后,耦合系数与时延采用如下公式计算得到:
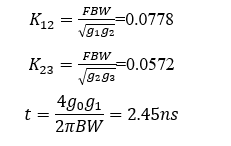
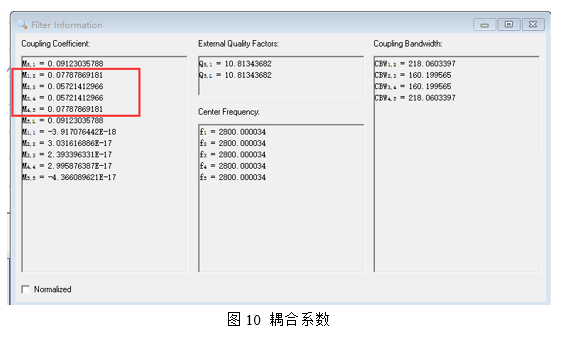
第二种方法就是直接调用Couplefila或者CST Filter Designer 3D的数据,如下图所示:
4.2 依据中心频率与Q值仿真出单个谐振器尺寸
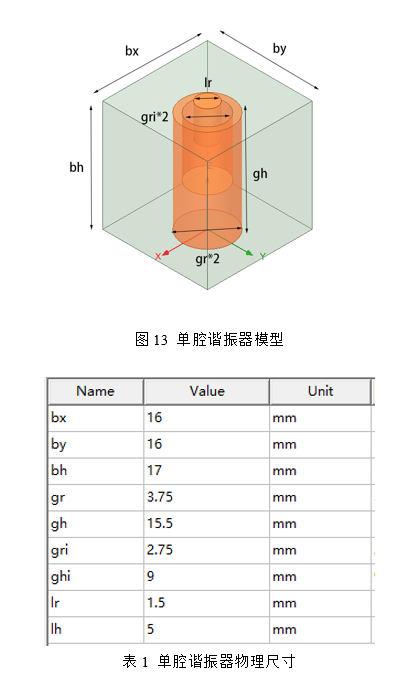
当前所设计的滤波器中心工作频率为2.8GHz并且Q=2000,单腔的结构由空气腔与谐振杆组成,空气腔高度取值依据滤波器中心工作频率对应自由空间1/8波长入手,或者保持电长度在60度以下即可,空气腔的长与宽依据Q值大小决定,若保持材料与腔壁电导率一致,一般空气腔的尺寸越大Q值越高。如图11所示,腔体高度若取17mm对应电长度为57deg,若设计的产品在高度方面有严格的限制,腔体的高度取值较小也可以,只需在HFSS软件里面仿真出对应当前腔体高度的谐振器尺寸,同时满足Q值要求即可。若腔体宽为16mm,谐振杆的直径可取7.5mm,谐振杆尺寸的取值可依据同轴线特征阻抗计算方法,一般没有功率和高Q值要求,以50Ω入手。若要求高功率,阻抗按30Ω设计,若要求高Q值,从75Ω入手。
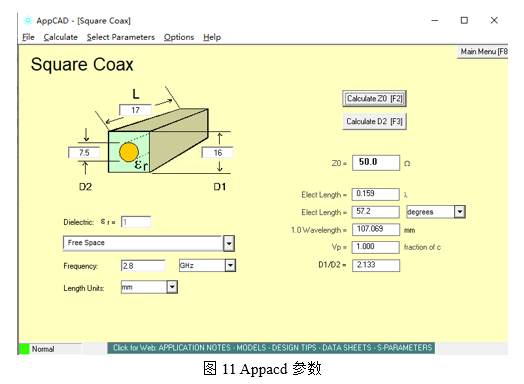
依据腔体高度17mm,腔体宽度16mm,谐振杆直径7.5mm在HFSS中建立3D仿真模型,优化各个尺寸参数使当前仿真模型谐振频率为2.8GHz同时Q值在2000以上。一般用于同轴腔体滤波器的材料有铝、铜、铁和银等金属,不同材料对应不同的电导率。如果用银作为腔体与谐振器主材料,Q值最大,但是性价比不高。因此考虑成本控制,常规使用铝作为腔体材料并在其表面涂镀3-7um的银层即可。这样即能实现生产成本的控制,同时也能实现高Q值的要求。
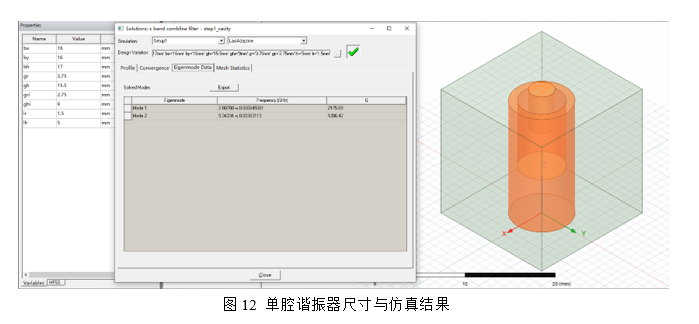
最终仿真优化好后的谐振器尺寸如图13,各个参数尺寸如表1所示:
4.3 依据耦合系数,扫描对应耦合结构尺寸
谐振器与谐振器之间的耦合系数定义为Kij,其中i和j表示谐振腔序号。如K12表示谐振器1与谐振器2之间的耦合系数。当前所设计的滤波器阶数为n=5,表示有5个谐振器和4个耦合系数,耦合系数分别为K12、K23、K34和K45,由于滤波器对称性,其中K12=K45,K23=K34,因此只需要仿真得到K12和K23即可。耦合系数的仿真由双模法确定,即在HFSS本征模求解器中设置2个模式,利用公式(4)来确定:
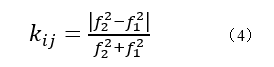
建立如如下图14所示的耦合仿真模型,此模型依据单腔谐振器确定的尺寸,通过仿真扫描两谐振器之间的距离Sij来对应计算的耦合系数。
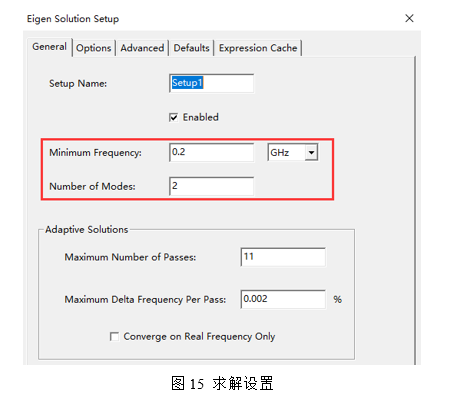
耦合仿真模型的求解设置中Minimum Frequency设置为0.2GHz,Number of Modes设置为2,如图15所示:
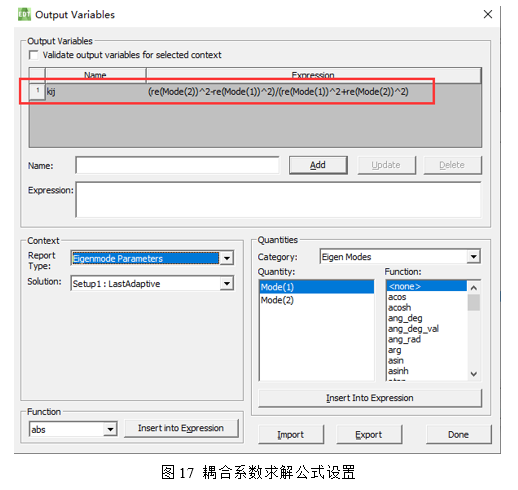
然后将谐振器之间的间距S设置为扫描变量如图16所示,在Calculations设置Output Variables中耦合系数求解公式:(re(Mode(2))^2-re(Mode(1))^2)/(re(Mode(1))^2 re(Mode(2))^2)如图17所示:
仿真完成后的结果如图18所示,将耦合系数对应间距结果如表2所示:
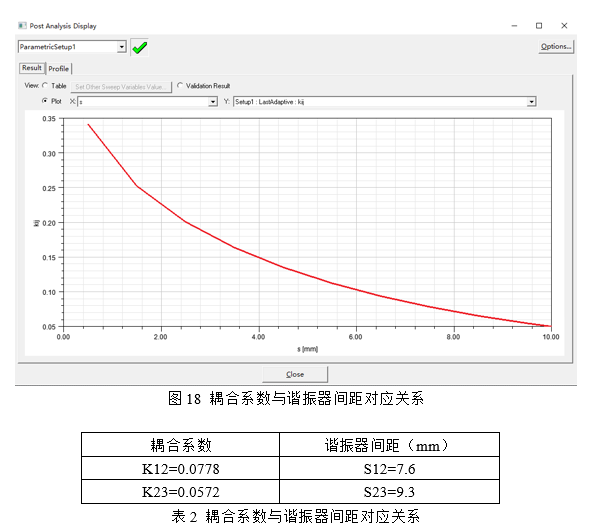
4.4 依据外部Q值或者时延,设计输入输出结构
依据计算得到的输入输出时延t=2.45ns,建立如图19所示的直接耦合输入输出结构,抽头距离地高度为ch,调谐螺钉的深度为lh,通过调试ch的高度对应计算得到的时延,通过调节lh对应中心工作频率2.8GHz。
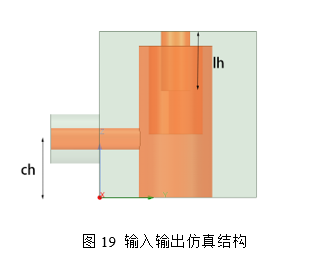

当时延满足在2.4ns并且时延波峰为中心工作频率2.8GHz时,抽头高度ch=6mm,调谐螺钉的尺寸lh为6.1mm。
4.5 建立整体仿真模型
通过前面单腔谐振器仿真、耦合仿真和时延仿真,综合所得的初始尺寸如下表3所示,然后建立如图21全仿真模型:

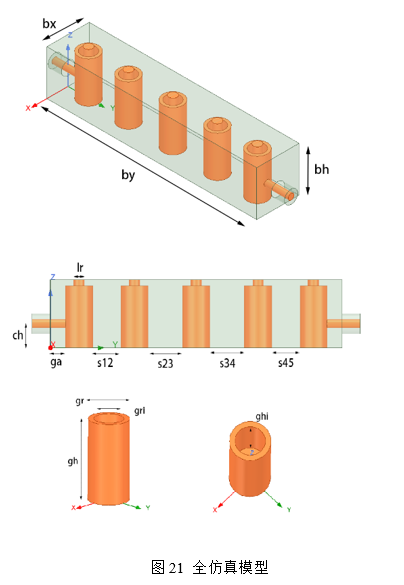
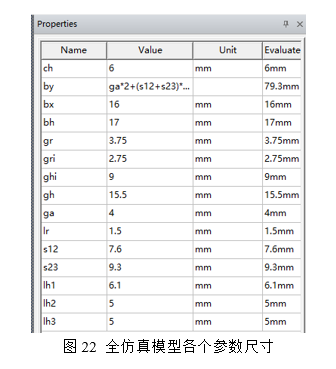
由于谐振器1与谐振器5频率受抽头影响这里重新定义调谐螺钉为lh1,lh1的尺寸由时延仿真确定为6.1mm,中间谐振器2与谐振器3的尺寸由单仿真时确定的尺寸为lh2=5mm和lh3=5mm,如图22所示:
求解设置的频率Frequency为2.8GHz,迭代次数和求解精度保持默认数值如图23所示,扫频范围设置为1.4-4.2GHz如图24所示:

全仿真模型的创建与各个参数设置完成后,运行仿真可查看得到由综合所得的参数仿真所得的S参数如图25所示:
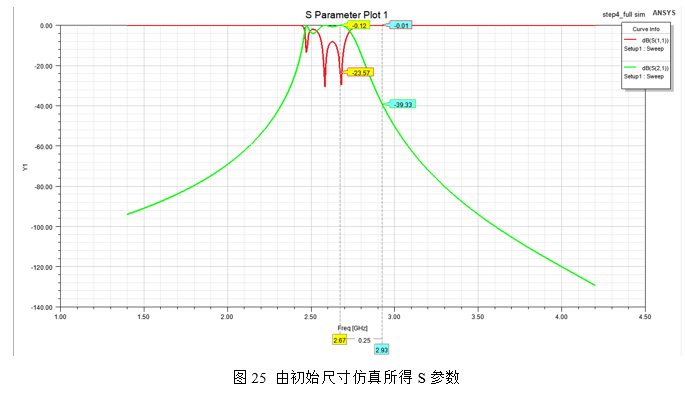
此时可以观察得到,滤波器有基本的S21与S11响应,但是由综合所得参数仿真的全仿真模型的S参数离所需求的中心频率2.8GHz有一定的频偏,主要表现为往低频偏移。很多朋友将仿真做到这一步就会反问为什么前面的综合步骤在如此严谨的情况下,滤波器最终仿真波形为什么不是如理想的Couplefila响应一样?此时我们需要明白的一点,前面综合过程中的单腔仿真、耦合仿真与时延仿真所得参数并不代表最终的数据,它只是一个初始尺寸,因此要将滤波器响应完全和理论曲线对应就需要接下来介绍的调试与优化过程。
4.6 滤波器调试
很多朋友在综合过程完成后,运行第一次仿真后就设置优化目标,让软件自动运行优化。虽然此种方法在原理上可行,但是软件能完成最终的优化满足设计只能看运气。因此这里给大家介绍一种调试方法。由图25所示的仿真曲线的通带,可以得到当前仿真模型离目标指标还有一定的差距,主要表现为往低频偏移。此时,调试第一步:调试谐振频率,先将通带频率调试到目标范围。如图26所示将调谐螺钉lh1、lh2和lh3的总体尺寸减小0.7mm后,运行仿真可得第一次调试结果如图26所示:
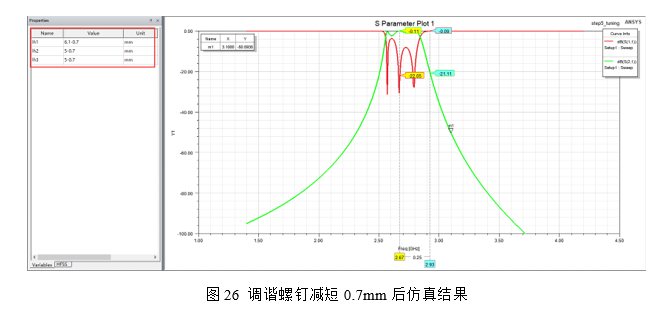
此时可以看到,滤波器响应曲线整体往高频率移动了一段距离,但是离目标范围仍然有一定的差距,因此需要继续减短调谐螺钉尺寸,再次减短lh1、lh2和lh3的总体尺寸0.7mm仿真曲线如图27所示:
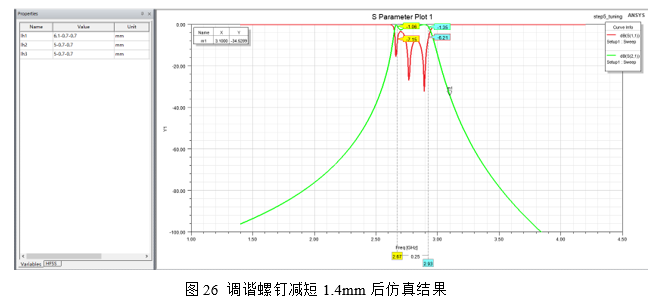
调试结果可以看出此时的通带已经在目标范围,就暂时停止对频率的总体调试。观察波形可以看出,此时滤波器回波损耗很差,只有-2dB,在不变动其它耦合尺寸和抽头高度的情况下。对滤波器频率lh1和lh5进行调试,因为这两个频率影响最深远的就是回波损耗。将lh1尺寸加大0.7mm,仿真如图27所示:
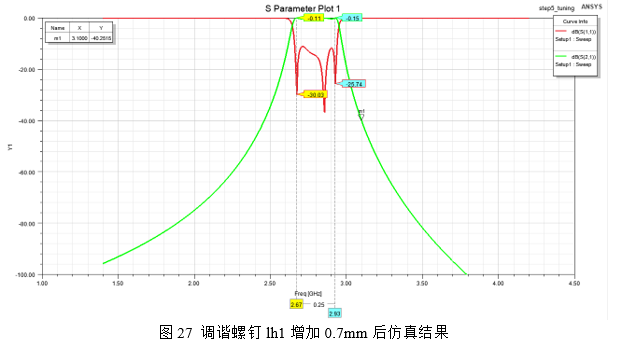
此时可以看出,滤波器的回波损耗基本能满足-12dB,如果是回波损耗要求不高的情况,此时的仿真曲线已能满足系统要求。如果是需要较高的回波损耗要求,此时在经验不足的情况下并不能判断当前模型的耦合尺寸与时延的修改值,因此需要设置优化来达到目的。
4.7 滤波器优化
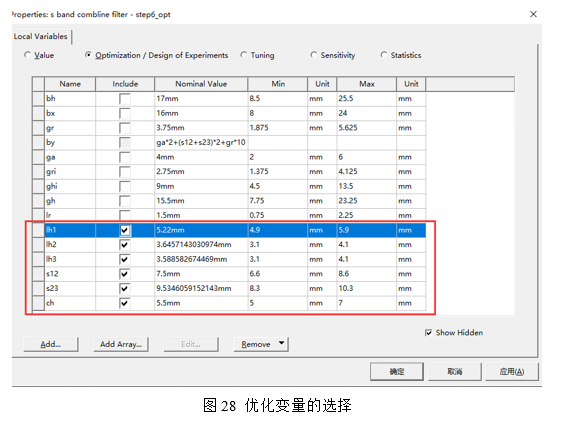
设置优化的变量,滤波器的影响因素主要就三个方面:频率、耦合与时延。lh1、lh2和lh3对应频率,s12与s23对应耦合量大小,ch数值对应时延大小。因此需要优化的参数就这6个数据,在参数变量中的Optimization窗口中勾选这6个参数如图28所示:
然后在Optimetrics窗口添加优化控件如图29所示:
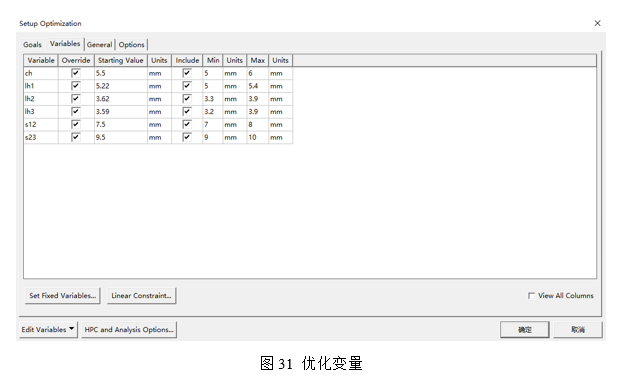
优化控件中设置优化目标为dB(S(1,1))<=-22,频率设置为通带工作频率2674-2926MHz如图30所示,然后在变量Variables中选择优化变量如图31所示:

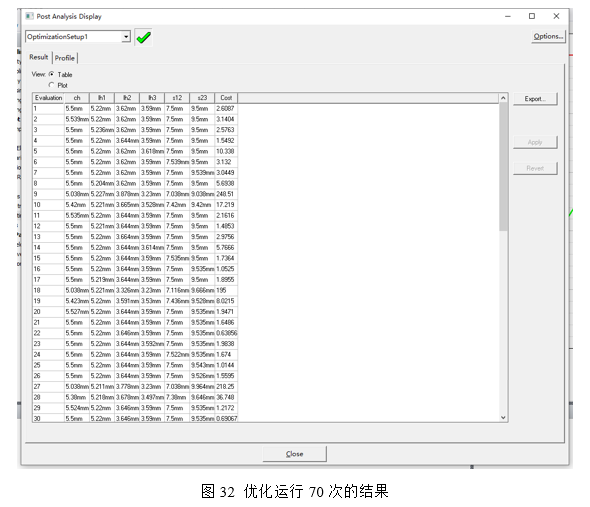
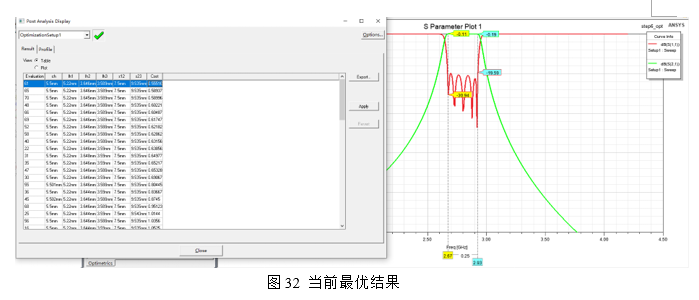
完成所有的优化设置后,运行仿真。可以看出在软件优化进行了70次计算下,此时的最优数值Cost为0.55516(cost越靠近0越好)如图32所示,选中cost为0.55516的数据点击运用,可以看出当前的仿真数据如图33所示:
5、总结
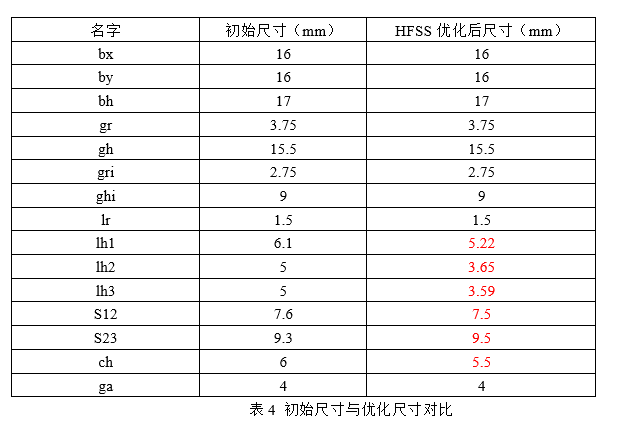
最终优化后数据与综合的数据对比如表4所示,红色是存在差异的尺寸,主要是调谐螺钉尺寸、谐振器间距和抽头高度。这三类参数代表的分别是频率、耦合与时延。因此这也解释了为什么综合数据第一仿真的结果并不能满足目标要求,需要设置优化的目的。
针对当前这篇文章的视频课程,大家感兴趣可以点击下面的链接进行学习。
https://www.fangzhenxiu.com/course/2942734-prcharge/







