算例分享:柱面拱壳的非线性屈曲分析
本节以一个拱壳的非线性屈曲分析为例,介绍非线性屈曲的分析方法。
1.问题描述
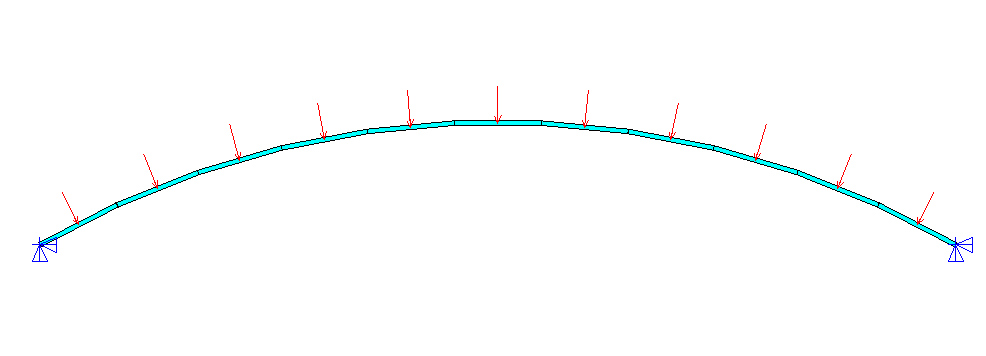
顶部承受均匀外压的钢圆柱拱壳,如图所示。拱壳两底端支座水平跨度为20m,拱壳跨过的圆心角为60度, 拱壳的半径为20m,拱壳轴线长度为36m,拱壳厚度为0.1m,左右两侧线约束三向线位移。计算此圆柱壳的极限承载能力。
2.建模及特征值屈曲分析
具体的操作过程采用批处理方式,命令流如下。
|
/FILNAME,Buckling |
!进入前处理器 |
|
/TITLE, Buckling ANALYSIS |
|
|
/PREP7 |
|
|
ET,1,181 |
|
|
MP,EX,1,2e11 |
!定义弹性模量 |
|
MP,PRXY,1,0.2 |
!定义泊松比 |
|
MP,DENS,1,7800 |
!定义材料密度 |
|
sect,1,shell |
|
|
secdata, 0.1,1,0.0,5 |
|
|
Secoffset,MID |
|
|
CSYS,1 |
!柱坐标系设为当前坐标系 |
|
k,,20.0,60,0.0 |
!建立关键点 |
|
k,,20.0,60,36.0 |
|
|
k,,20.0,120,36.0 |
|
|
k,,20.0,120,0.0 |
|
|
A,1,2,3,4 |
!通过关键点建立圆柱面,柱坐标系形成柱面 |
|
/VIEW, 1 ,1,2,3 |
!改变视图角度 |
|
/REP |
!重新绘图 |
|
aatt,1,,1,,1 |
!单元属性设置 |
|
AESIZE,ALL,2 |
!单元尺寸设置 |
|
MSHAPE,0,2D |
!单元形状设置 |
|
MSHKEY,1 |
!划分方式为映射网格划分 |
|
AMESH,ALL |
!划分网格 |
|
EPLOT |
!绘制单元 |
|
CSYS,0 |
!指定当前坐标系为总体直角坐标系 |
|
NSEL,S,LOC,X,-10.1,-9.9 |
!选择受约束节点 |
|
NSEL,A,LOC,X,9.9,10.1 |
|
|
D,ALL,UX |
!约束三向线位移 |
|
D,ALL,UY |
|
|
D,ALL,UZ |
|
|
ALLSEL,ALL |
!恢复选择全部对象 |
|
sfe,all,1,pres,,1 |
!对全部单元施加单位压力 |
|
/PSF,PRES,NORM,2,0,1 |
!压力显示为箭头 |
|
/REP |
!重新绘图 |
|
FINISH |
!退出前处理器 |
施加了位移约束及单位压力的模型如图所示。

按照如下的命令执行特征值屈曲分析。
|
/SOLU |
!进入求解器 |
|
antype,static |
!静力分析类型 |
|
pstres,on |
!预应力刚度选项 |
|
Solve |
!求解 |
|
FINISH |
!退出求解器 |
|
/SOLU |
!进入求解器 |
|
ANTYPE,1 |
!指定分析类型为特征值屈曲分析 |
|
BUCOPT,LANB,6,0,0 |
!设置屈曲模态提取方法及模态提取数 |
|
MXPAND,6,0,0,1,0.001, |
!设置屈曲模态扩展数及扩展算法选项 |
|
SOLVE |
!执行特征值屈曲分析 |
|
FINISH |
!退出求解器 |
|
/POST1 |
!进入通用后处理器 |
|
SET, FIRST |
!读入第一子步的计算结果 |
|
*GET,LScale,ACTIVE, ,SET,FREQ |
!获取第一屈曲特征值 |
|
PLDISP,0 |
!第1阶屈曲变形 |
|
SET,NEXT |
!读入下一子步的计算结果 |
|
PLDISP,0 |
!第2阶屈曲变形 |
|
SET,NEXT |
!读入下一子步的计算结果 |
|
PLDISP,0 |
!第3阶屈曲变形 |
|
SET,NEXT |
!读入下一子步的计算结果 |
|
PLDISP,0 |
!第4阶屈曲变形 |
|
SET,NEXT |
!读入下一子步的计算结果 |
|
PLDISP,0 |
!第5阶屈曲变形 |
|
SET,NEXT |
!读入下一子步的计算结果 |
|
PLDISP,0 |
!第6阶屈曲变形 |
|
FINISH |
!退出后处理器POST1 |
3.非线性屈曲分析
具体求解过程采用批处理方式,命令流如下。
|
/PREP7 |
!进入前处理器 |
|
TB,BISO,1,1,2, |
!修正材料模型 |
|
TBDATA,,2.0e8,0 |
|
|
UPGEOM,0.05,1,1,'Buckling','rst' |
!引入几何缺陷 |
|
FINISH |
!退出前处理器 |
|
/SOL |
!进入求解器 |
|
ANTYPE,0 |
!指定分析类型为静力分析 |
|
sfscale,PRES,1.2*LScale |
!压力荷载缩放 |
|
time,1.2*LScale |
!指定载荷步结束时间等于所施加荷载 |
|
NLGEOM,1 |
!打开大变形选项 |
|
OUTRES,ALL,ALL |
!输出所有子步的全部结果 |
|
lnsrch,on |
!打开线性搜索 |
|
NSUBST,200, , ,1 |
!设置分析的载荷子步数 |
|
SOLVE |
!求解 |
|
FINISH |
!退出求解器 |
|
/POST26 |
!进入时间历程后处理器 |
|
CSYS,1 |
!切换至柱坐标系 |
|
n1=node(20,90,18) |
!选择跨中节点 |
|
NSOL,2,n1,U,X ,DEFLECTION |
!指定X方向位移变量 |
|
/AXLAB,X,Displacement |
!指定绘图横坐标标签 |
|
/AXLAB,Y,Load |
!指定绘图纵坐标标签 |
|
/GROPT,REVX,1 |
!曲线X轴反向 |
|
XVAR,2 |
!指定横坐标表示变量2(位移) |
|
PLVAR,1 |
!绘载荷-位移曲线 |
|
FINISH |
|
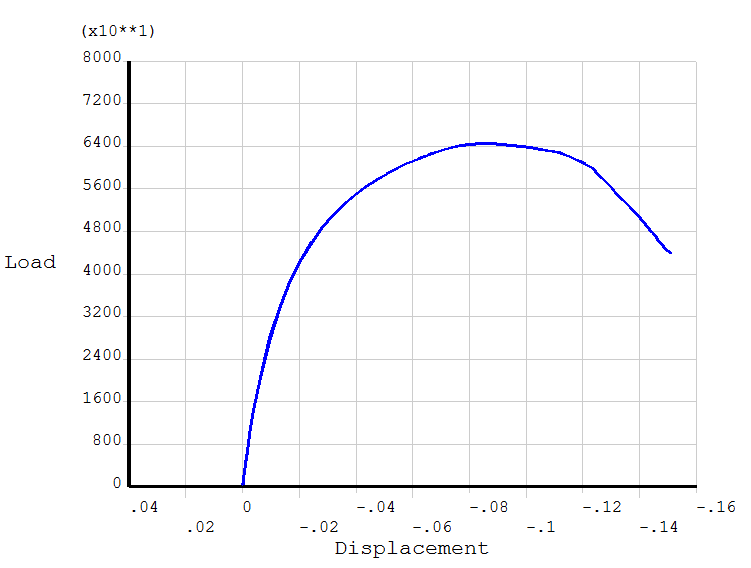
执行上述命令流,得到压力-壳顶水平位移曲线如图所示。

在前面的网格划分中在壳顶位置处没有节点,实际上这可以通过改变网格划分参数使得壳顶恰好有节点。本例题中不再重新修改网格参数,后处理中选择一个最靠近柱壳顶部的节点,提取其位移即可,实际后处理中选择的节点是最靠近柱坐标系下坐标值(20,90,18)的节点。在上述曲线中可以看到,在最后一个收敛子步的压力值位于60000到70000之间,低于第一阶屈曲特征值80193.7961。
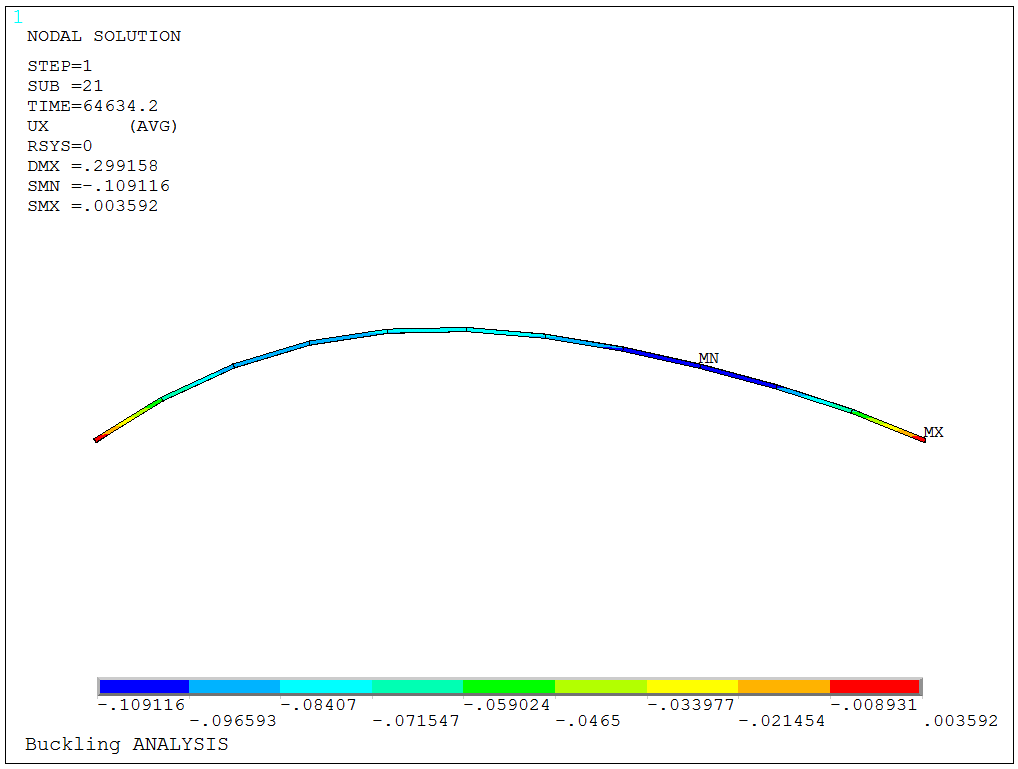
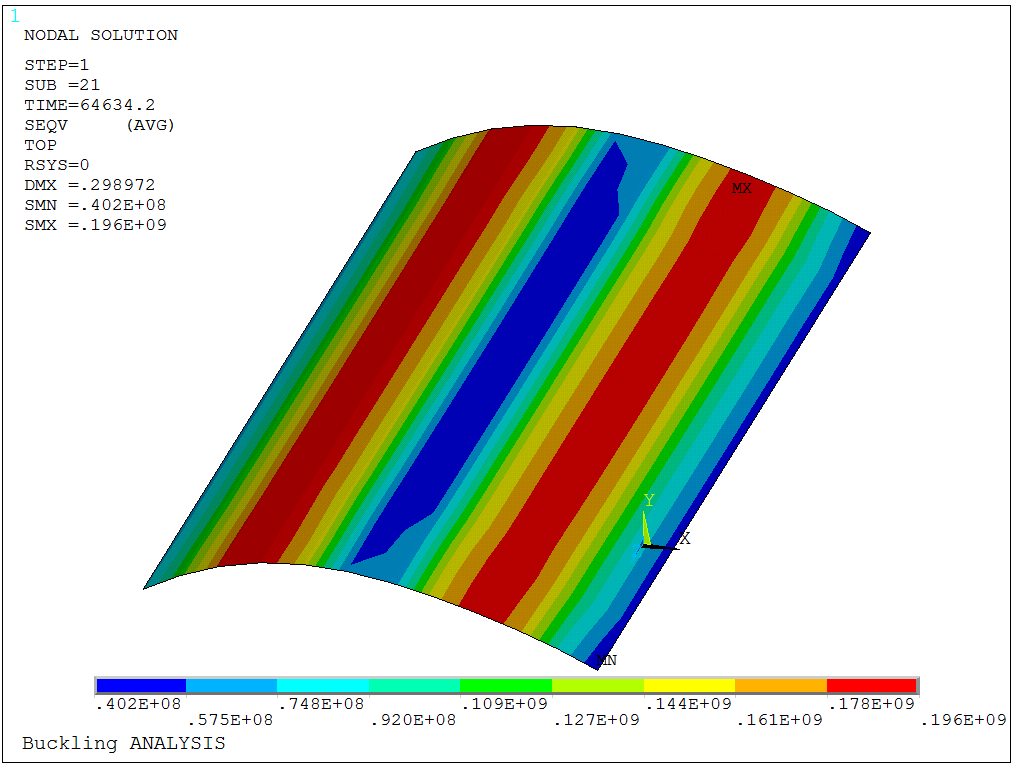
通过上图的结构变形可以看出,拱壳结构在达到极限荷载时,变形沿着拱的轴线呈现反对称分布的特点。这一分布与所施加的几何缺陷,即第一阶屈曲特征变形的分布式一致的。
由上图的应力分布可以看出,结构中局部应力已经基本上达到200MPa的屈服点,由于节点应力是临近单元应力的平均值,因此判断结构已经进入弹塑性工作阶段。下图为塑性应变的分布情况。
为了模拟后屈曲行为,采用弧长法计算非线性屈曲,非线性求解阶段的命令流请参考附件。
注意:上述命令是在修正了弹塑性材料参数及增加了几何缺陷之后执行。
在命令中采用了拱壳顶部水平位移限值0.15m,计算完成后,采用与之前线性搜索方法相同的后处理方式,得到荷载-位移曲线如图所示。
弧长法计算得到了后屈曲行为,捕捉到了曲线的下降段。64488Pa,与前述方法最后收敛子步对应的载荷64634Pa相比,仅相差约0.23%。