转子动力学系列(一):临界转速与坎贝尔图
本文摘要(由AI生成):
本文主要介绍了转子动力学的概念、研究内容、运动方程、临界转速计算方法以及ANSYS APDL和ANSYS Workbench两种分析方法。转子动力学是固体力学的分支,主要研究转子-支承系统在旋转状态下的振动、平衡和稳定性问题,尤其是研究接近或超过临界转速运转状态下转子的横向振动问题。临界转速是转子动力学中的重要概念,是指转子系统在旋转过程中出现共振现象的转速。临界转速的计算方法包括理论解和数值解,其中理论解主要考虑轴的弯曲不计轴的质量,加上回转效应时的频率方程,数值解则通过ANSYS APDL和ANSYS Workbench两种分析方法进行求解。两种分析方法均能得出较为准确的结果,但ANSYS Workbench分析方法在求解过程中需要更多的计算资源。
转子动力学为固体力学的分支。 主要研究转子-支承系统在旋转状态下的振动、平衡和稳定性问题,尤其是研究接近或超过临界转速运转状态下转子的横向振动问题。转子是涡轮机、电机等旋转式机械中的主要旋转部件。
运动方程为:
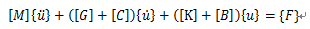
1.例子
如图刚性支撑单圆盘转子,圆盘质量m=20kg,半径R=120mm,转轴的跨度l=750mm,直径d=30mm。圆盘到左支点的距离a=l/3=250mm。求该转子临界转速及振型。(摘自《转子动力学》钟一谔 1987年 P14页 )
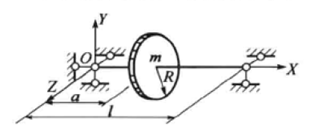
刚性支撑单圆盘转子
2.理论解
仅考虑轴的弯曲不计轴的质量,加上回转效应时的频率方程为
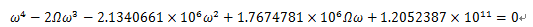


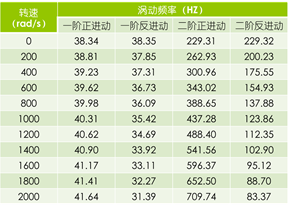

通过上述涡动频率可绘制出坎贝尔图,图中的曲线与直线的交点为该转子的一倍频临界转速,共有三个,故该刚性支撑单圆盘转子前三阶固有频率为:
2265.09 rpm
2333.85 rpm
8069.16 rpm
3.ANSYS APDL 分析
圆盘采用MASS21单元模拟,转轴采用BEAM188单元模拟,轴的两端为简支约束。其有限元模型如下图所示,求解可得到各阶涡动频率:

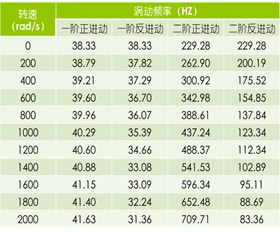
使用plorb命令输出各阶振型轨迹:
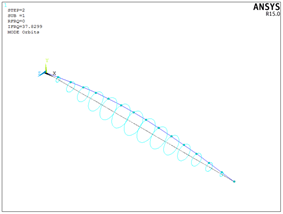
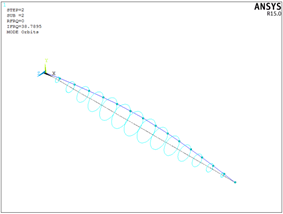
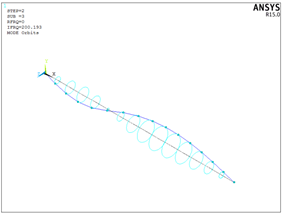
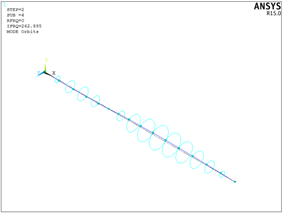
使用plcamp命令得到坎贝尔图:
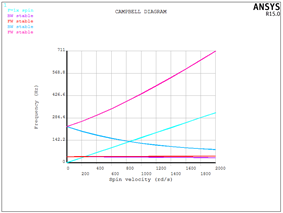
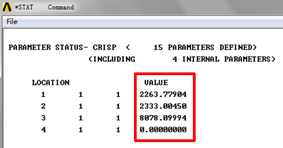
如上图得到前三阶临界转速为:
2263.8rpm
2333.0rpm
8078.1rpm
4.ANSYS Workbench分析
圆盘通过Point Mass模拟,转轴在DM里面通过直线绘制赋予截面的方式模拟,轴的两端为简支约束。其有限元模型如下图所示,求解可得到各阶涡动频率:

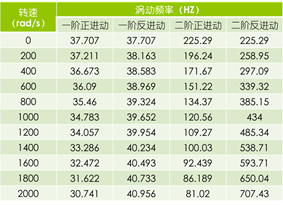
在Solution中导出前四阶振型如下:
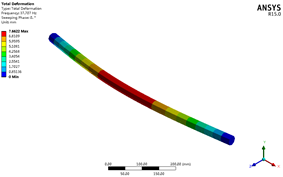
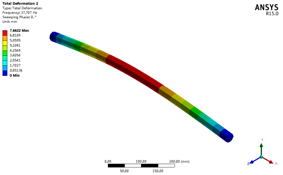
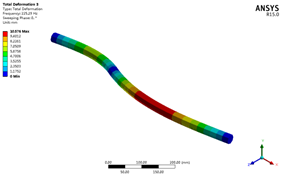

点击Campbell Diagram输出坎贝尔图:
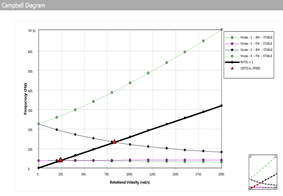

如上图得到前三阶临界转速为:
2226.4rpm
2293.8rpm
7928.1rpm
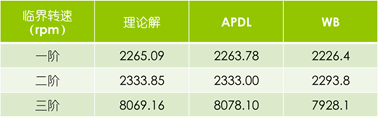
5.结果对比
误差范围内,APDL和WB的精度均满足需求。读者可采用三维模型求解与一维模型结果对比,若圆盘没使用Point Mass模拟而采用直接实体模型,得到的振型图与一维模型结果略有差异。
6.附录(命令流)
finish
/clear
/prep7
m=20
r=0.12
l=0.75
a=0.25
d=0.03
et,1,beam188
et,2,mass21
mp,ex,1,2.058e11
mp,prxy,1,0.0
sectype,1,beam,csolid
secdata,d/2
jd=m*r*r/4
r,2,m,m,m,2*jd,jd,jd
k,1
k,2,a
k,3,l
k,4,l/2,a
l,1,2
l,2,3
latt,1,,1,,,4,1
esize,0.05
lmesh,all
dk,1,uy,,,,uz,ux
dk,3,uy,,,,uz
d,all,rotx
type,2
real,2
n1=node(a,0,0)
e,n1
finish
/solu
nmod=4
antype,modal
modopt,qrdamp,nmod,,,on
mxpand,nmod,,,yes
coriolis,on,,,on
solnum=11
*do,i,1,solnum
omega,(i-1)*200
solve
*enddo
finish
/post1
set,list
plcamp,on,1,rds
转子动力学系列(二):基于ANSYS APDL的不平衡响应分析
转子动力学系列(四):基于ANSYS Workbench的不平衡响应分析
转子动力学系列(五):不同建模单元对比(BEAM188与SOLID186)
转子动力学系列(六):不同轴承单元对比(COMBIN14和COMBI214)
转子动力学系列(十):轴对称实体单元Solid272/Solid273的应用














