理解结构力学:总结几何不变体系组成规律
来源:头条号 新叔的科学日常。
之前我们了解了,一个结构体系按照几何是否可变被分为几何可变体系与几何不变体系,其中几何可变体系又有常变体系与瞬变体系之分。经过前面的内容,我们对体系的划分以及可变体系的分析进行了介绍分析,自然的,我们将要开始几何不变体系的讲解。
本文首先要强调,我们通过前面的内容知道,几何不变体系其实也存在类别划分,此处读者只用从约束的角度来考虑即可,即按此几何不变体系是否存在多余约束来分类。接下来的内容涉及的都是无多余约束的几何不变体系的组成规律,这里只讨论平面杆件体系最基本的组成规律,更复杂的结构以及分析会随着结构力学基本功的提高,后面会有所补充涉及。
01一个点与一个刚片
以这个组成规律开头可以很好的复习之前的内容,我们先假想一个自由点,它存在两个自由度(水平分量,竖直分量),我们将刚片假设为基础(结构力学中基础是最常见的刚片),那么怎样的约束能让此自由点和刚片(基础)联结后变为几何不变体系呢?根据前面自由度的结论:一个支杆可以减少一个自由度,可知我们用两根链杆将自由点与刚片(基础)相连后,自由度会变为0,可是自由度为0并不代表几何不变(自由度大于0代表几何可变)。比如下面的结构类型中,自由点尽管被两根链杆相连,但却是瞬变体系。
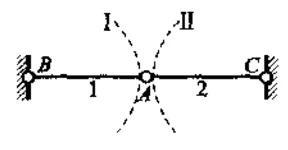
上例中,读者不必把B和C两处看作独立的两部分,基础在无穷远处是相交的,将B和C看作是一整体即可。所以,通过上面的分析我们可以得到两个限制条件,来得到关于点和刚片组成无多余约束的几何不变体系联结点一般规律结论:
一个点与一个刚片用两根链杆相连,且三个铰不在同一直线上,则组成几何不变的整体,且没有多余约束。
需要强调的是,我们此处几何不变的整体指的是几个连接“部件”之间相对稳定。
02两个刚片之间的联结方式
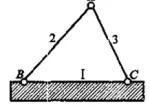
通过刚才点与刚片联结的例子入手,我们把这个体系中的2杆假想成一刚片,即变成了下面这样的形态:
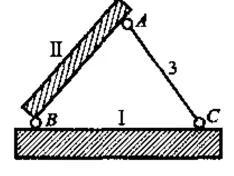
通过观察上面的情况,很容易得到下面这个结论:
两个刚片用一个铰和一根链杆联结,且三个铰不在同一直线上,则组成几何不变的整体,且没有多余约束。
3三个刚片的联结方式
我们可以在上面例子的基础上继续延伸,此处直接给出结论:
三个刚片用三个铰两两相连,且三个铰不在一直线上,则组成几何不变的整体,并且没有多余约束。
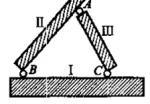
4两刚片被三链杆连接
两个刚片用三根链杆相连,且三链杆不交于一点,则组成几何不变的整体,并且没有多余约束。
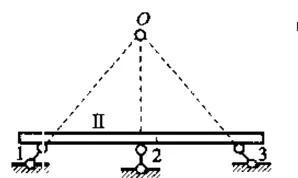
我们可以反过来看上面的这条规律,假如交于一点会发生什么?如果把O点看作圆心,那么很容易发现,所有支杆都指向了圆心,并且所有支杆都能绕固定端,沿着目前与杆垂直的方向转动(切线方向)。那么,此刻体系中所有的支杆都在转动瞬间具有“同向转动”的趋势且不相互约束。但在转动瞬间过后,变得不再同向变形转变为几何不变体系,所以这种体系为几何瞬变体系。(平行的三根链杆也看作会在无穷远处相交)





