Journal of Computational Physics丨物理神经网络:气体输送问题案例
作者:Erik Laurin Strelow, Alf Gerisch, Jens Lang, Marc E. Pfetsch
单位:德国达姆施塔特工业大学数学系
01 摘要
最近提出了物理神经网络,并为求解微分方程提供了一种新的有前途的方法。它们已经适应了更多的场景,并提出了原始方法的不同变体。在这个案例研究中,我们回顾了其中的许多变化。我们专注于能够补偿损失函数失衡的变量,并将这些变量与天然气输送问题的应用进行全面的数值比较。我们的案例研究包括损失函数的不同公式、不同的算法损失平衡方法、不同的优化方案以及不同数量的参数和采样点。我们得出的结论是,在损失函数中 特别选择恒定权重的原始PINN方法在我们的测试中给出了最好的结果。这些权重是通过计算昂贵的随机搜索方案获得的。对于我们的测试案例,我们进一步得出结论,为其他微分方程开发的损耗平衡方法对气体输送问题没有好处,控制体积物理信息公式对初始公式没有好处,最佳优化策略是L-BFGS方法。
02 图表简介
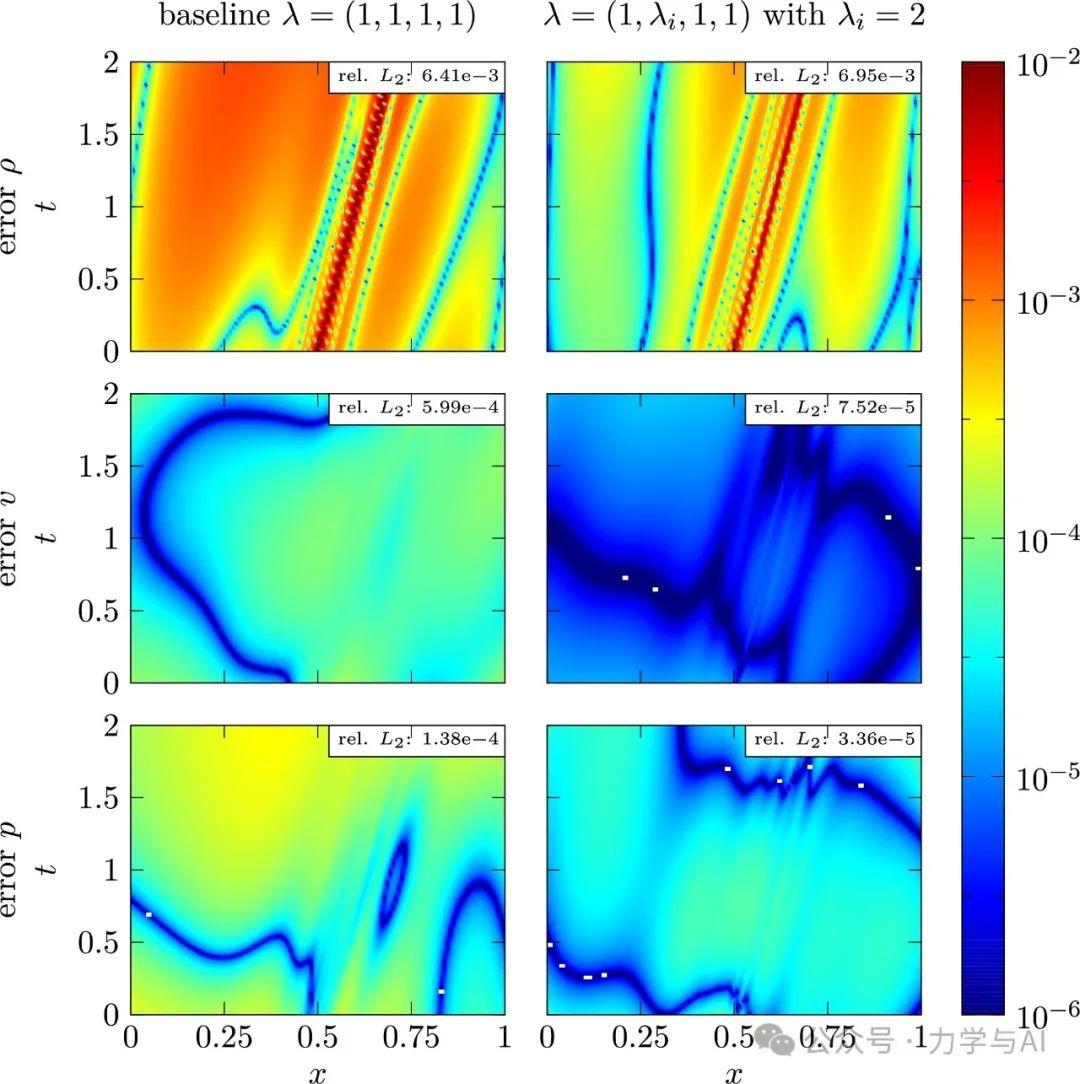
图:训练的两个模型在不同权重λ下的误差比较
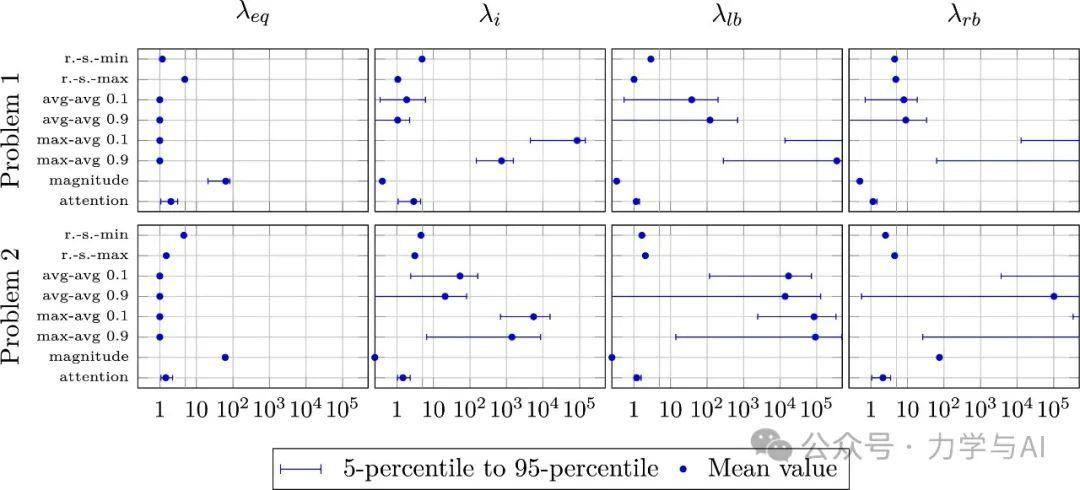
图:Adam优化算法(具有学习率衰减)权重的可视化

图:L-BFGS方法优化;通过随机搜索方法找到的最佳(rnd-search-min)和最差(rnd-earch-max)权重
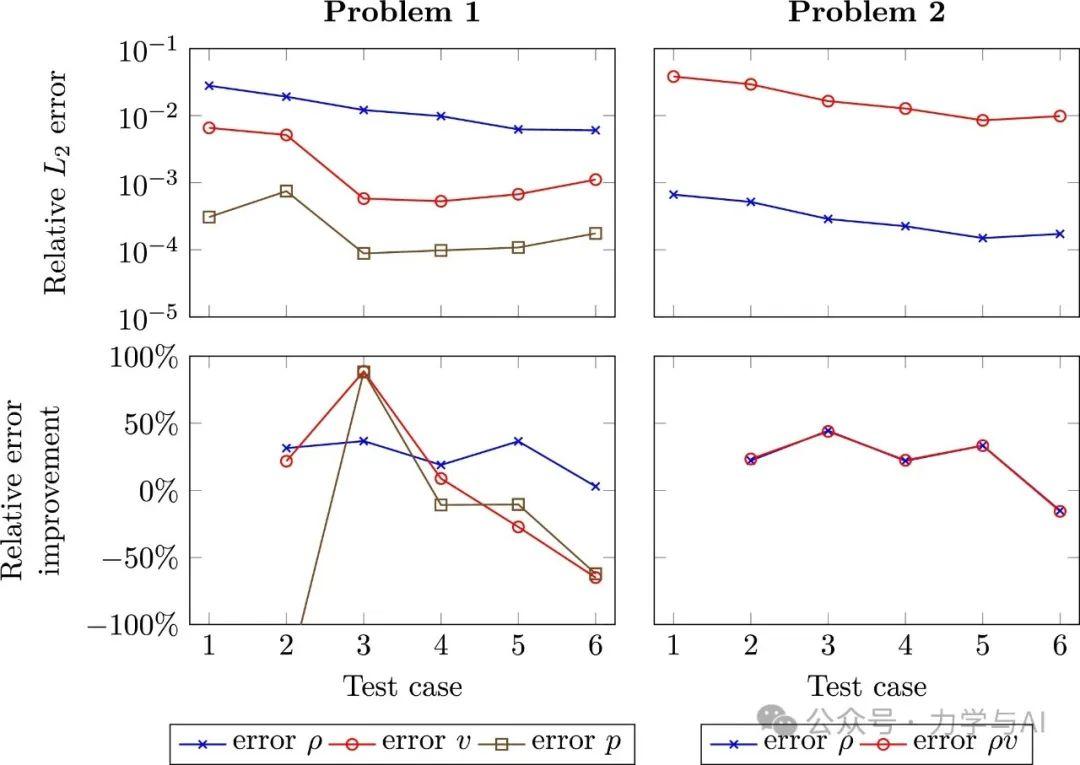
图:测试结果
03 结论
在这篇文章中,我们对气体输送问题的物理信息神经网络进行了全面的案例研究。我们提供了不同方法之间的客观比较,以获得近似两个测试问题的气流的神经网络。我们的目标是提供关于如何有效地获得这些神经网络以及在这个特定用例中可以预期的结果的知识。我们想利用这些知识来开发降阶方法,即PINN,它可以避免冗余计算,对于类似的模拟来说是快速的,并且可以保持高精度。这一点很重要,因为这些模型及其近似解构成了天然气管网模拟的构建块,因此也构成了天然气管网优化和最优控制的构建块。因此,在这些更复杂的气体网络设置中,具有适当精度的高效近似方法对于进一步发展最先进技术至关重要。原始物理信息方法的一个主要困难是需要解决多目标训练问题才能获得近似值。单独的目标源于分别执行微分方程、初始数据和边界数据。训练问题的单目标损失函数是通过形成单个项的加权和来获得的。这将困难转化为这些权重的选择,使得损失函数中的各个项被适当地平衡。处理这个问题一直是我们案例研究的中心点之一。在这里,我们的测试表明,在物理知情损失函数中选择适当的权重对于获得误差最小的神经网络非常重要。我们的最佳权重是通过随机搜索方案确定的,该方案随机选择一个权重列表,为每个选择的权重训练一个神经网络,然后选择训练误差最小的神经网络。然而,这个过程在计算上非常昂贵,并且由于权重与问题有关,因此当问题发生变化时,必须重复该过程。文献中提出了许多策略(损失平衡方法),以在训练过程中动态确定这些权重。这种策略已经成功地应用了,比最初的基于物理的方法有所改进,但适用于与我们的案例研究不同的微分方程。与原始方法相比,这些方法通常具有较小的计算开销。我们已经测试了其中的几种策略,但没有一个测试问题的解决方案比随机搜索方案和原始物理知情方法确定的解决方案更好,而且大多数都明显更差。这导致了一个重要的结论,即这些方法不适用于一般的一类微分方程,并且气体输送问题可能会带来这些方法没有认识到的独特挑战。我们还建议,未来关于损失平衡方法的工作应该包括与随机搜索方案的比较。此外,我们还测试了控制体积物理信息方法——一种基于守恒定律积分形式的公式。与最初的物理知情方法以及损耗平衡扩展相比,这种方法具有一些理论优势。这里,通过考虑积分形式,可以降低积分维度,还可以避免损失函数中的自动微分以及上述确定权重的问题。这些优势伴随着实现开销的增加。然而,这是另一个重要的结论,在我们的测试案例中,该方法的性能优于基于微分形式的原始物理信息公式。此外,在这些测试中,确定性求积规则的性能优于随机蒙特卡罗求积规则。我们还考虑了三种不同的训练程序,包括Adam方法、L-BFGS方法和两者的混合方法。我们在测试中得出结论,L-BFGS单独使用最少的迭代产生了最好的结果。然而,结合算法加权方法,我们观察到了一些受益于混合方案的情况。如果我们考虑到案例研究的所有结论,我们建议使用L-BFGS方法训练的原始物理方法,通过神经网络获得管道中气体流动问题的最佳近似值。如果计算预算允许,我们强烈建议执行随机程序,以确定最佳损失平衡权重。基于物理的神经网络的最大优势之一是能够灵活地将该方法适应不同的用例或在实现中交换构建块,如优化方法或求积规则。在这里,像这样的案例研究对于提出最有希望的前进道路非常重要。我们的测试表明,为了获得高度准确的近似值,我们需要在训练阶段以非常高的精度解决优化问题,而且更准确的求积规则可以提供更好的结果。然而,在传统的机器学习任务中,人们避免以高精度解决训练问题,以避免过度拟合。因此,我们的观察为PINN提供了新的研究方向,这些方向偏离了传统的机器学习。我们看到了PINN的两个进一步研究方向,这可以为我们在管道中气体输送的特定应用带来进展,也可以为更普遍的问题设置带来进展。首先,双曲守恒律是否存在限制所考虑的损失平衡方法适用性的特定性质?如果是,如何克服这些障碍?第二,我们能否确定哪些PINN扩展特别适用于哪些PDE问题,并理解为什么?这两个方向都旨在更深入地理解PDE中编码的底层物理与其在神经网络中的表示之间的联系。
04 参考文献
Strelow E L, Gerisch A, Lang J, et al. Physics informed neural networks: A case study for gas transport problems[J]. Journal of Computational Physics, 2023, 481: 112041.










