结构非线性分析理论-(1)
第一章 引言
绝大多数连续介质力学问题都可以表述为边界值问题。在这类问题中,我们需要规定连续体边界上的条件,并关注如何确定边界值以及物体内部某些物理量的分布情况。在结构力学问题中,这些物理量通常是位移、速度、应力和应变,但只要问题表述合理,任何其他物理量(¹其他物理量可以是物体内的温度分布、相或物质的给定浓度、电荷分布等)都可以作为物体内部的未知量。边值问题(BVP)的传统表述包含三个不同的方程"族",即平衡方程、运动学方程和本构方程。在接下来的章节中,我们将使用有限变形理论介绍这些方程的形式,讨论以位移场为主要未知量的连续体情况。1.1 边界值问题的强形式和弱形式
考虑一个一般连续体的空间构型,其在初始状态(t=0)占据体积V₀,质量密度为ρ₀,这定义了其参考状态。该物体受到单位质量体力b和单位面积表面力t的共同作用。物体外表面上受到表面力作用的部分称为St。此外,物体表面的另一部分Su(²注意Su∩St=∅且Su∪St=S)上存在已知位移ū。经过时间间隔Δt后,物体变形并占据体积V,质量密度为ρ,被表面S包围。平衡方程(³假设不存在动态效应,因此加速度场a可忽略)用柯西应力张量表示为:
其中D为变形率张量,对应于速度场v。可变形材料由如下一般形式的本构定律控制:
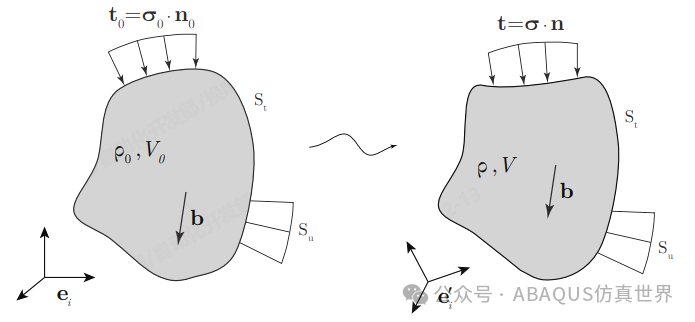
图1.1:一个任意形状的物体在参考态和变形态下受到应力场和位移边界条件的作用
其中σ̌代表σ的Jaumann速率,通常用于描述发生有限变形和转动的固体的本构行为,L是已定义的速度梯度张量。我们还引入边界条件S:u = ū = 已知值 在Su上 (1.4)
t̂ = σ·n = 已知值 在St上 (1.5)方程(1.1-1.5)构成了边界值问题的强形式。该问题包含15个未知量,即位移场3个(u)、速度梯度张量L六个和应力张量σ六个。我们也可以引入另一种表述方式。首先,我们用一个标量方程⁴替代(1.1)中的三个平衡方程。该方程通过将(1.1)中的微分方程与虚速度场δv*(任意但连续可微)相乘,然后在连续体的整个体积上积分获得: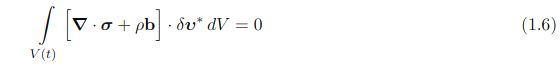
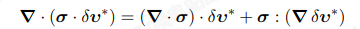
利用散度定理⁵(也称为高斯定理),我们也可以写出: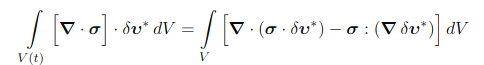
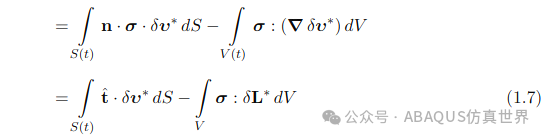
其中δL是对应于虚速度场δv的速度梯度张量。让我们将δL分解为其对称部分δD和反对称部分δW*,并利用σ的对称性可以写出⁶(回想一下,对称张量和反对称张量的双点积等于零):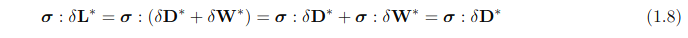
现在结合方程(1.6),(1.7)和(1.8),我们可以用以下替代形式: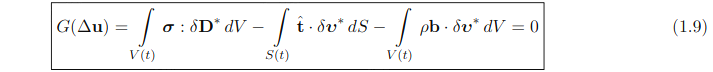
上述表述也被称为边值问题的弱形式,它为下一节将要介绍的有限元近似提供了基础。1.2 有限元近似
在有限元设置中,解从 tn 到 tn+1 逐步发展,需求解的主要未知数是位移增量 Δu(x)。一旦确定了 Δu,则计算当前增量结束时 t = tn+1 处的总位移场为: un+1(x) = un(x) + Δu(x) (1.10) xn+1 = X + un+1(x) (1.11) 将连续体离散为有限元,我们将未知位移增量 Δu 表示为每个单元内的函数插值:
其中 [N(x)] 是由用户定义的“形状”函数(该近似值最早由 Galerkin 引入)组成的插值矩阵,而 {ΔuN} 是节点位移的向量。现在回想一下,虚拟速度场 δv* 必须与所有运动学约束兼容。然而,在 (1.12) 中引入的插值将位移约束为具有某种空间变化,因此 δv* 也必须使用相同的函数插值来定义 [Abaqus 理论手册]。因此,
虚拟应变率张量 δD* 也以数组形式表示为:

其中 [B(x)] 是包含形状函数 Nα(x) 空间导数的矩阵,意义为 。最后,我们将中其余量的数组表示法引入弱形式 (1.9) 为:
。最后,我们将中其余量的数组表示法引入弱形式 (1.9) 为:
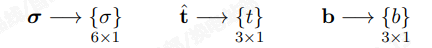
代入 (1.9) 中的每个项,我们得到:
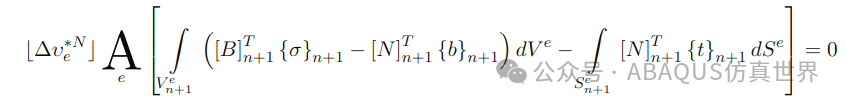
其中 Ve 和 Se 分别是所考虑有限元的体积和表面,而 Ae 表示“组装”操作。然而,由于上述表达式必须对所有 成立,我们可以推导出:
成立,我们可以推导出:
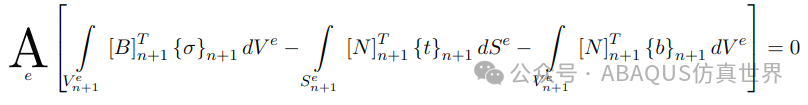
现在让我们定义包含牵引力和体力的外载荷向量:
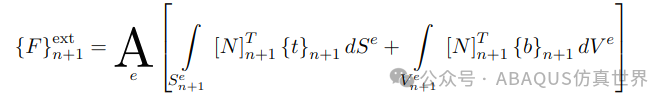
此时,回想一下 {σn+1} 是未知量 {ΔuN} 的非线性(一般)函数,因此我们写为:
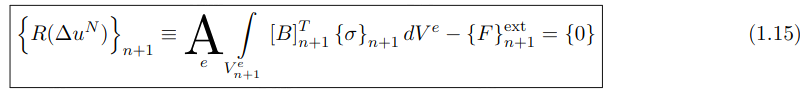
其中 {R(ΔuN)}n+1是表示内力σn+1和外力tn+1、 bn+1之差的残差向量。弱问题的解是位移场 {ΔuN},它满足方程组 (1.15),或者等价地,在 t = tn+1 时使外载荷 {Fe} 等于内力 {σn+1} 的位移场,从而产生小于给定容差的残差。 方程组 (1.15) 是关于节点位移的高度非线性系统,主要有两个原因。首先,位移通过本构定律  形成与应力的非线性关系。其次,也是在这里讨论中最重要的是,在有限变形理论中,我们考虑了参考几何和当前几何之间的偏差,通过积分极限引入了几何非线性,因为一般情况下 Ve = Ve(u)。
形成与应力的非线性关系。其次,也是在这里讨论中最重要的是,在有限变形理论中,我们考虑了参考几何和当前几何之间的偏差,通过积分极限引入了几何非线性,因为一般情况下 Ve = Ve(u)。



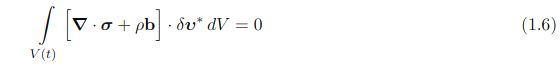
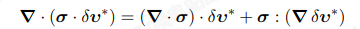
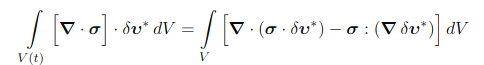
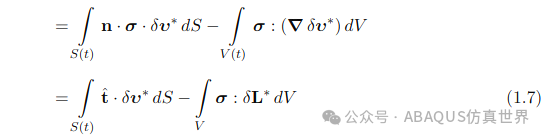
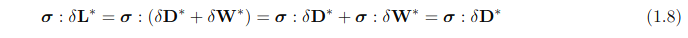
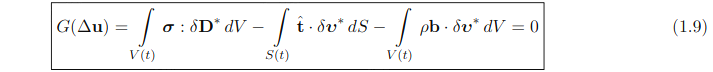



 。最后,我们将中其余量的数组表示法引入弱形式 (1.9) 为:
。最后,我们将中其余量的数组表示法引入弱形式 (1.9) 为: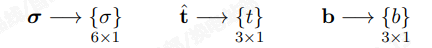
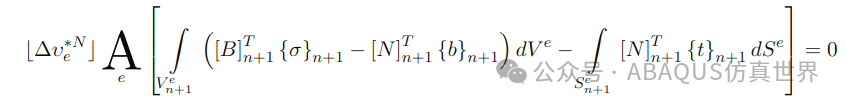
 成立,我们可以推导出:
成立,我们可以推导出: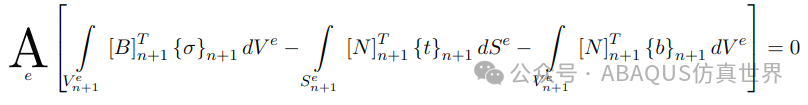
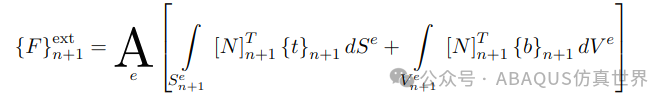
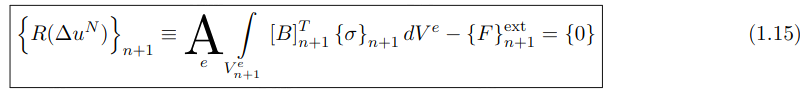
 形成与应力的非线性关系。其次,也是在这里讨论中最重要的是,在有限变形理论中,我们考虑了参考几何和当前几何之间的偏差,通过积分极限引入了几何非线性,因为一般情况下 Ve = Ve(u)。
形成与应力的非线性关系。其次,也是在这里讨论中最重要的是,在有限变形理论中,我们考虑了参考几何和当前几何之间的偏差,通过积分极限引入了几何非线性,因为一般情况下 Ve = Ve(u)。




