流体仿真中,六面体(Hex)网格的求解效率真的比四面体(Tet)高”很多”么?
本文摘要(由AI生成):
本文主要讨论了六面体网格和四面体网格在流体仿真中的优劣。文章首先指出,六面体网格在流体仿真中具有优势,但具体优势包括求解效率高、数量少、精度高、算得准、没有伪扩散、守恒性好等。接着,文章对六面体网格和四面体网格的求解效率进行了对比,发现当表面网格数量一致时,六面体网格和四面体网格的求解效率相当。最后,文章给出了一些简单的结论,包括体网格数量少不一定代表优势、六面体与四面体体网格数量比例为1:2.3时求解速度相同但四面体占用内存更高、仿真分析要有理有据等。
流体仿真中,六面体(Hex)网格与四面体(Tet)网格的争论一直伴随着整个CFD的发展过程,坊间也流传着许许多多关于六面体网格、结构化网格、四面体网格、甚至是Cutcell网格等相关内容的种类繁多的观点。由于CFD的工程性质,很多问题并不需要工程师进行过于深入、过于细致的研究,大家往往还是会把关注的重点放在仿真问题的求解之中,不管六面体还是四面体,只要能解决问题,就都是好网格!
但是值得一提的是,对于绝大多数的流体仿真工作者,都有一个共识,那就是:六面体(结构化)的网格好!
具体来讲,六面体网格(Hex)到底好在哪呢?大概会得到以下几种答案:
● 六面体网格求解效率高
● 六面体网格数量少
● 六面体网格精度高、算的准
● 六面体网格中没有四面体那样的伪扩散
● 只要是六面体网格就一定好用,cutcell也是六面体的一种
● 六面体网格守恒性好
● 四面体属于忽悠人的网格,不能用
● ……
不论对错,关于六面体网格的观点还是非常多、非常明确的;但由于篇幅的关系,我们可能没有办法一一的对上述观点进行分析和讨论;所以,本文仅对上述观点中的第一条进行相对详细的分析和介绍,那就是:在公平的条件下,六面体网格和四面体网格,谁的求解效率高?

问题的分解与明确
● 公平的条件如何界定?
● 求解效率高是通过什么方式体现的呢?
采用案例测试的方式进行,使用相同的计算机和相同的算例设置,仅网格不同(采用replace方式更换),初步估计稳态计算1000个迭代步,通过计算的真实时间来判定求解效率。
● 求解之前的内容(如网格划分、网格输出、求解设置、算例保存、网格替换等),暂不列入判定范围
● 仅比较纯六面体网格和纯四面体网格在 Fluent 中的计算效率
通常的流体仿真工作是必须包含边界层的,因为纯四面体在近壁面附近求解精度相对较低;不过,本次测试为了避免非四面体的层状网格(Prism)对最终的求解产生影响,所以采用了完全一致的网格类型进行对比。
知识要点复习
★ 六面体网格的优势
● 采用六面体网格可以减小网格数量
● 对于流动方向沿着网格的问题,六面体网格可以减小数值误差
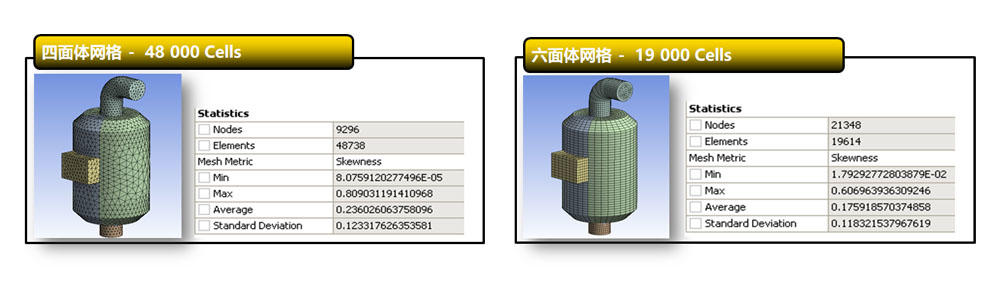
通常情况下,六面体网格数数量更少
★ 六面体网格的劣势
● 几何形状复杂时工作量极大(能力 & 耐心)
● 几何曲率较大时,网格质量难以有效控制
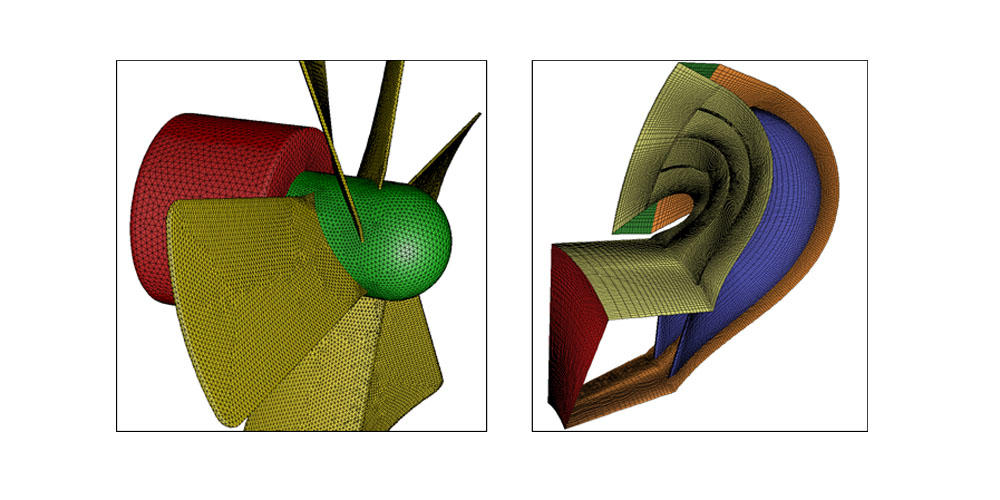
需要注意的是:有一些相对复杂的几何模型在生成六面体网格的时候会产生质量很差的网格,而且只能通过网格加密才能有效改善。
随着网格的加密,六面体网格的数量反而超过了自动生成的四面体数量……

当网格方向与流动方向对齐的时候,六面体可以极大的减小数值误差

当网格方向与流动方向不一致的时候,六面体的数值精度与四面体一致
公平的条件
比赛之前,必须要指定规则;同样的道理,六面体与四面体的网格对比也需要一个公平的条件,那么这个公平的条件指的是什么呢?有三个备选选项:
● 网格边 (edge) 的长度一致
● 网格面 ( face ) 的面积一致
● 网格单元的体积 (cell) 一致
★ 边 (edge) 的长度一致


通常情况下,对于边(edge)长度相等的hex与tet ,体网格数量之比约为1:5~1:8
★ 面 ( face ) 的面积一致


当三角形与四边形面积相等时,边长的比例约为1.3~1.5
★ 体积 (cell) 一致

体积一致,也就意味着六面体与四面体的体网格数量相等
为了能够确认这个公平的条件,我们还专门进行了一些问卷的调查,结果如下:


总体来讲,大家的意见还是相对分散的,为了公平起见,我们将选择多数工程师的意见“面 ( face ) 的面积一致”作为相对公平的评判标准。

表面网格(face)面积一致的纯六面体网格与纯四面体网格
求解的结果
|
对比条件 |
六面体 |
四面体 |
|
表面网格数量(一致) |
105000 |
105532 |
|
Cell |
1.25M |
3.04M |
|
Face |
3.80M |
6.22M |
|
Node |
1.31M |
0.54M |
|
.msh 文件大小 |
116 MB |
131 MB |
|
峰值内存占用 |
5.85 GB |
9.63 GB |
|
1000步计算时间 |
10637 s |
11487 s |
当面网格数量一致时,我们可以得到以下结论:
● Hex 与 Tet 体网格数量比约为 1:2.5
● Hex 与 Tet 网格文件大小比例约为 1:1.13
● Hex 与 Tet 求解效率比例约为 1.08:1
● Tet 占据内存更大
因此,在相对“公平”的条件下,六面体网格的求解效率可以认为和四面体一致!!
相信对于大多数流体仿真工程师来讲,这是一个颠覆性的结论;当然,也有很多人会说上面所谓“公平”的前提条件并不完全公平,所以结论并不合理;无论如何,这些都是可以接受的观点。
还是引用作者最常用的一句话,文章的目的并不是要否定别人的观点、也并不希望一定能够说服大家,而仅仅是从某些特定的角度,提供一些信息,希望能够引发大家的思考。
一些简单的结论:
● Fluent 采用的是有限体积法,因此,体网格的数量在很大程度上代表了计算区域的离散精细程度,从这个角度来讲,网格数量少,也不一定是优势。
● 简单的讲,当六面体与四面体体网格数量比例是1:2.3时,两者的计算效率(求解速度)是一致的,但四面体求解时占用内存更高(约1.6倍)。
● 仿真分析要有理有据,提出观点不能人云亦云。
作者:张杨 流体高级工程师 仿真秀专栏作者
声明:原创文章,首发仿真秀;部分图片源自网络,如有不当请联系我们,欢迎分享,禁止私自转载,转载请联系我们。

.jpg?imageView2/0/w/120/h/120)
.jpg?imageView2/0/w/90/h/90)




