知否知否?常用振动诊断方法——包络分析和阶次分析
来源:优感设备诊断中心微 信公 众号
本文摘要(由AI生成):
本文介绍了阶次分析在变转速齿轮箱振动信号分析中的应用。阶次分析通过等角位移重采样,将时域信号转换为阶次信号,从而消除转速变化对频谱分析的影响。文章详细阐述了阶次分析的实现过程,包括同步采集振动信号和转速信号、鉴相时标的计算以及振动信号的重采样。通过阶次分析,可以清晰地识别出与机械旋转相关的谱线,有效弥补稳态工况下频谱分析的不足。文章最后通过一个实际案例展示了阶次分析在变转速齿轮箱振动信号分析中的效果,证明了阶次分析在变速工况下的优越性。
包络分析
对于各个行业,存在很多低转速设备。低转速部件引起的振动集中在低频部分,且往往较为微弱,容易淹没在其他信号中,在频谱中不容易分辨出故障信号与噪声信号。但这种故障引起的冲击信号往往会激起高频固有频率,在频谱上表现为出现共振带,即低频故障信号作为某高频载波的边频出现。因此,对于这种出现调制现象的故障信号,往往需要通过包络进行分析诊断。

图1 包络解调机理
解调前需要对信号进行滤波处理,通过带通滤波,去除不相关频率,仅保留载波频率附近的信号(如下图保留区域)。载波频率往往存在多个,除齿轮啮合频率外,各个零部件的固有频率较难进行精确测量,但发生共振的频带往往是高频带。因此,通常预处理的方法是进行高通滤波,去除低频的不相关频率,仅保留高频部分,再进一步做包络解调处理。

图2 带通滤波

图3 高通滤波
下图为某轴承出现外圈故障时的时域波形和频谱。时域波形中,波形较为嘈杂,没有出现明显的冲击信号。频谱图中,3KHz到5KHz的范围内具有明显的调制现象,这是由于轴承损伤产生的冲击激起了轴承零部件的固有振动。利用一个通带为3-5KHz的带通滤波器对原始信号进行滤波,然后对滤波信号进行包络谱分析。
在包络谱中,可以清晰的看到234Hz的谱线及其多个倍频。234Hz与理论计算的此轴承的外圈故障特征频率236Hz很接近,表明轴承出现了外圈故障。该案例说明了基于包络解调分析的诊断方法具有很强的实用价值。

图4 时域波形

图5 加速度频谱图

图6 包络谱图
阶次分析
在稳态工况下,对振动信号进行频谱分析,可以有效地揭示被分析信号在全过程中的频率成分,但无法反映频率随时间变化的规律。对于某些设备的变速工况,尤其低速端需要采集较长时间的信号,若对长时间采集的振动信号仍然采用频域分析,会造成频谱上峰值能量分散,出现谱线模糊的现象,如下图所示。阶次分析是分析变速工况信号的有效方法。

图7 谱线模糊现象
以三级行星齿轮箱为例,第三级大齿轮的齿数为102,小齿轮的齿数为27,低速轴与高速轴的传动比为1:3.778,假设低速轴转频为fl,根据传动机理可知,高速轴转频fh=3.778fl,齿轮副啮合频率GMF=102fl,频谱示意图如下图所示。但是由于频谱分析无法揭示信号频率随时间变化的规律,所以一旦转速不稳定,振动信号的频谱中就会出现“模糊”现象。

图8 谱线模糊现象
然而,对于结构确定的齿轮箱,即使转速发生变化,齿轮箱中各部件特征频率之间的比例关系不会改变。如上例,无论低速轴的转速如何变化,高速轴转频fh 和啮合频率GMF始终是低速轴转频fl 的3.778倍和102倍,该倍数就是阶次。阶次是指以某转轴作为参考轴,其他轴的转频相对于参考轴的倍数。
通常阶次与对应的振动频率之间的关系如下:

式中,O 为阶次 (Order),fn(t )为参考轴转频,f(t )为监测部件的转频。
对于参考轴本身,其转频阶次为1。在稳态工况下,f(t )为常数,fn(t )也为常数,频谱分析可以较好的表达振动信号的特征。在变速工况下,f(t )和fn(t )都随时间t 变化而变化,由于传动结构固定,阶次O 作为比值固定不变,因此变速工况下,阶次分析可以进行很好的弥补稳态工况下频谱的不足。
从上面的分析可以看出,阶数与频率有直接对应关系,与频率一样揭示了振动信号频率结构。在上例中,以低速轴作为参考轴(阶次为1),那么不论低速轴转速如何变化,高速轴的旋转阶次都是3.778,啮合阶次为102。
阶次分析实际上是对原始时域信号重采样,将等时间间隔采样变为等角度间隔采样。因此,阶次分析的关键是实现振动信号的等角度采样,即根据参考轴的转速变化相应的调节采样率,这个过程就是阶次跟踪。为最大化减小误差,通常采用高速轴作为转速参考轴。
阶次技术实现的过程:
同步采集振动信号和转速信号,其中振动信号通过加速度传感器采集,转速脉冲信号通过转速计获得;
利用转速脉冲信号拟合转轴转角和时间的函数关系,计算振动信号角域重采样的时刻值,即鉴相时标;
最后对同步采集的振动信号进行重采样,采用数据插值方法计算重采样时刻对应振动信号的幅值,得到等角度采样信号,即阶次信号。如下图:

图9 阶次技术原理
通过等角位移重采样,将时域波形转换成为阶次波形,这样就建立起了稳态工况下的信号分析方法与非稳态工况下的信号分析方法之间的桥梁。对阶次波形可进一步按照稳态工况下的方法进行分析,分别得到阶次谱、阶次包络波形、阶次包络谱。

图10 阶次技术分析技术
稳态工况中,时域波形表示信号随时间的变化,因此横坐标单位是时间 (s);变速工况中,与之对应的是阶次波形,阶次波形表示信号随参考轴旋转转数的变化,因此横坐标单位是参考轴转数 (n)。
稳态工况中,频谱是由时域波形经过FFT变换得到,横坐标单位是频率 (Hz);变速工况中,与之对应的是阶次谱,阶次谱是阶次波形通过FFT变换得到,其横坐标单位为阶次 (Order)。
稳态工况中,包络波形是时域波形经过gPK包络处理得到,横坐标与时域波形相同,为时间 (s);变速工况中,与之对应的是阶次包络波形,阶次包络波形可看成是阶次波形经过gPK包络处理得到,横坐标与阶次波形相同,为参考轴的转数 (n)。
稳态工况中,包络谱是由包络波形经过FFT变换得到,横坐标单位是频率 (Hz);变速工况中,与之对应的是阶次包络谱,阶次包络谱是阶次包络波形通过FFT变换得到,其横坐标单位为阶次 (Order)。
某变转速齿轮箱,对低速端振动信号与转速信号同步采集,采集时长为60s,可以看到转速从1430-1630r/min波动。对原始振动信号直接进行频谱分析,看到频谱中出现了严重的“能量分散”现象,不能有效识别与机械旋转相关的谱线。进行阶次分析后得到阶次波形和阶次谱,阶次波形以高速轴作为参考,横坐标为高速轴转数 (n)。在阶次谱中,可以清晰的看到高速端转频阶次,以及低速轴啮合阶次及调制边频。
从该案例中可以明显看出,对于运行在变转速工况下的设备,频谱分析不能有效反映出频率随时间的变化,因此出现谱线模糊现象。而阶次分析消除了这种影响,可以清晰的看到各旋转部件的阶次谱线,如下图所示:

图11 振动信号时域波形
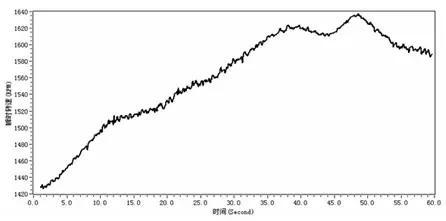
图12 转速信号

图13 阶次谱








