Comsol电力变压器漏磁场分布及损耗计算

5月前浏览4180

摘要

正文

关键词：电力变压器；漏磁场；电磁损耗；有限元；数值计算

1.变压器漏磁场

1.1漏磁场

漏磁通，一般指变压器中的漏磁通。在变压器中，凡不按铁芯所规定的磁路流动的一切其他磁通，称为漏磁通。简单来讲，变压器就是通过公共磁场耦合的两个或多个线组，这个公共磁场将能量(电压或电流信号)从一个绕组(初级)传送到另一个绕组(次组)。当有交流电通过一个绕组时，就会产生磁场，磁场通常用磁力线来表示。磁力线经过的是磁阻(电抗)最小的路径，当有交流信号在初级线圈中形成闭合回路时，初级绕组的磁通就会在次级绕组中感生出电流，然而，并非初级绕组产生的所有磁通都会通过次级绕组，并未同时通过初、次级绕组的磁通称为漏磁通。

变压器中的漏磁场是由多种因素引起的，包括铁心构造及制造不完美、绕组的空隙以及其他因素如变压器周围的绕组、铁架以及空气中的磁阻和磁场耗散等。这些因素导致磁通在空气中形成闭合磁路，而不是完全通过铁芯耦合。

漏磁场的存在会引起一些问题，如高损耗、高电压尖峰等，它是变压器的一个重要参数。在设计变压器时，需要考虑到漏磁场的影响，采取一些措施来减小漏磁场，如采用高磁导率的铁芯材料、优化绕制方式等。

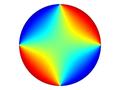
图1. 变压器漏磁场分布

1.2漏磁场有限元计算

有限元法是一种求解偏微分方程解的计算方法，具有对复杂几何适应性好、计算精度高等优点，因而在电磁学、传热学和流体力学等领域广泛应用。有限元数值计算的基本流程为：首先，将求解域剖分成若干有限元网格；然后，运用插值基函数构造待求解量的近似解；最后，运用加权余量法或变分原理将偏微分方程进行转化，使其成为离散形式的代数方程。应用有限元法进行数值求解时，运用节点插值可得到求解域内任意点的场量。

有限元法可分为变分有限元法和伽辽金有限元法。变分有限元法基于变分原理，需找出一个与所求定解问题相应的泛函，使得这一泛函取得极值的函数便是该定解问题的解，从该泛函的极值问题出发进行离散化，得到相应的代数方程；伽辽金有限元法，即令场方程余量的加权积分平均值为零，利用伽辽金准则，用有限单元上的插值基函数作为权函数，导出离散化代数方程组，代数方程的解答就是有限元各节点上待求变量的值。其中伽辽金有限元法应用范围更加广泛，更易于概念上的理解。因此选择利用伽辽金有限元法对电磁场方程进行求解。

2.物理模型

根据油浸式变压器的实际尺寸，按照其铁芯高度，油箱高度，绕组的分布、位置以及尺寸，导线的电流、匝数等数据，选择在Comsol自带的建模软件模块变压器三维膜型，模型如图 2所示。模型中各部分结构材料均可在材料库中直接添加使用。仿真计算还需设置材料的相对磁导率、相对介电常数和电导率参数，仿真模拟同时需要添加铁芯材料的BH曲线，为了计算结果的准确性，以上参数均从相关资料以及现有实验数据中获得，如图3所示。

图2. 计算模型

图3. 材料参数设置

3.物理场边界条件

变压器漏磁场和电磁损耗选择ACDC的磁场模块进行计算，通过给高低压绕组施加电流激励，可以得到变压器内部漏磁场和电磁损耗，详细物理场边界条件设置如图4所示。

图4. 物理场边界条件

根据有限元法的求解原理，剖分越精细，求解越准确，所以在计算绕组漏磁场时需要对尺寸较小的绕组区域进行网格加密处理。同时，为了保证整体场域网格剖分的质量，在初步剖分和部分加密后还需要进行整体场域的网格优化，主要对场域内几何边界处的网格进行平滑处理。具体剖分过程如下：利用 AFM 进行网格初始化；对绕组等区域进行三角形网格加密；采用 Laplace 网格光顺技术对边界网格进行平滑处理，网格剖分如图5所示。