Abaqus基础 | 从数学原理到有限元思想的萌芽
质点、刚体和变形体
我们从所学习的力学知识谈起,首先从质点、刚体、变形体的概念来切入,引出五类力学的知识区域。
所谓质点,源于我们的中学力学,对象指的是无变形、无形状的一个质心,常由牛顿三大定律方程描述。
所谓刚体,源于我们的理论力学,考虑了研究对象的形状,关键涉及到了由于对象自身转动引起研究问题变化的情况。
变形体来源于多门力学知识,比如材料力学,研究的是简单形状的小变形问题,如梁、杆,涉及的是线性和低阶微分方程的求解;结构力学研究是拥有众多数量且形状简单的小变形问题,如刚架、桁架,涉及的多是大规模的线性方程组;弹性力学就偏向于复杂形状的小变形问题,如壳、不规则几何体,基本单元取得是dxdydz微体;弹塑性力学就偏向于屈服、非线性等较大变形的问题。

这几大力学的基本变量及方程涉及三方面,即由变形方面描述的几何方程、力的平衡方面描述的力的平衡方程、材料特性方面描述的的物理本构方程。
变形体力学的要点
了解清楚质点、刚体、变形体后,接下来我们主要过渡到变形体力学方面的知识,这将是有限元发源的基础。
材料力学为了描述材料的力学行为,首先从同一材料的拉伸实验开始,把数据处理后引出了弹性模量的概念,形成了三大类变量——应力、应变与位移,消除了材料试样几何因素的影响,对材料本构进行了解释与构建。

接下来就转移到了对三大类方程的建立与求解中。几何方程描述的是位移与应变的函数关系;平衡方程描述的是力与应力的关系;物理方程描述的是应力与应变的关系,即材料本构属性。
微分方程的求解方法
对于实际问题,方程多为微方程,关于方程的求解方法有两大类:一类是解析方法,即通过函数关系的推导得出精确解;另一类是近似方法,如差分法与试函数法。
近似方法,步骤规范,容易编为计算机程序,以牺牲精度的方式,获取满足工程精度的结果,在实际工程中应用较多。
接下来我们以下面的一个实例进行方法介绍:

差分法,就是把这个对象分成若干段,把微分用有限差分代替,把导数用有限差商代替,从而把基本方程和边界条件近似地改用差分方程来表示,最终把求解微分方程的问题改换成为求解代数方程组的问题。


试函数法,它的思想就是假定有一个解,又称试函数,这个解中包含了待定系数,我们首先寻找满足边界条件的试函数,再把设定好的试函数带入控制方程,带进去之后基本不满足,我们再处理得到残差函数,通过使与原方程的误差残值最小,来确定试函数中的待定系数,得到最终的试函数,就得到了微分方程的解。


我们对三种方法进行比较,解析法技巧要求高,适用于简单问题,对于2D、3D问题很难得到解析解;差分法和试函数法求解过程规范,仅求解代数方程,容易用编程实现,适合工程中复杂问题的求解。
相对来说,试函数更为简单,计算量比较小,关键在于如何构造满足边界条件的试函数。也就引出了下面我们要说的问题:关于函数逼近的方式!

试函数与函数逼近
这里,关于试函数的问题,关键是要讨论函数的逼近问题。我们以一维函数为例,分析它的展开与逼近形式。
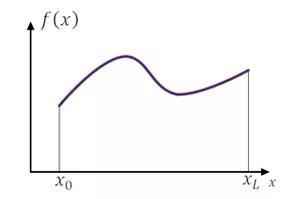
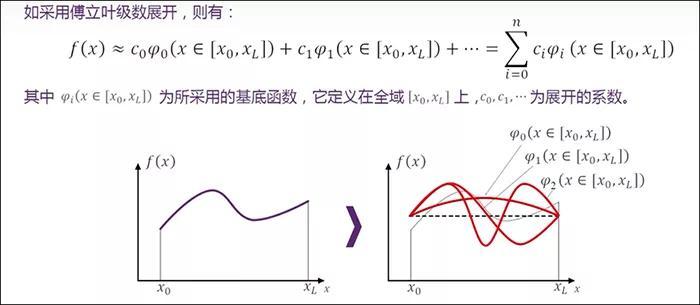
第一种是基于全域的展开形式:采用傅里叶级数展开,c 为待定系数,φ 为基底函数。我们可以用多个基底函数进行线性组合,去描述逼近目标函数。注意这儿的基底函数是定义在全域上的。
第二种是基于子域的展开方式:采用分段线性函数拼接出来整个目标函数,即不同的子域有不同的线性函数及系数,我们把每一段的线性函数组合起来得出结果。

对于两者的比较,前者基底函数高次连续,且仅采用几个函数就能得到较高的逼近效果,但是基底函数复杂,在2D、3D问题上去构造全域的基底函数是非常困难的;后者虽然在拼接处不连续,但是基底函数简单,形状逼近的确实还不错,且还能通过二次函数、三次函数进行逼近,提高精度,它的关键是如何针对复杂的2D、3D问题,构造出分片或者分块的试函数。
现在我们的方向是针对复杂几何域的函数表征及逼近。

针对于规则2D、3D形状,我们可以直接构造出全域的试函数,对于非规则形状,几乎就不可以了,只能通过分片和分块的方法构造试函数,去拼接成相近的形状。
有限元的核心原理
现在就很接近真相了,有限元的核心就是针对复杂几何域,采取分段、分片或者分块的方式,也就是子域的方式来构造相应的简单函数,然后再拼出一个全域的试函数。这种方式容易做得到。
我们从一个几何开始,进行几何离散,形状基本构件。我们把里面分出来的这些基本构件,像这些规范化的子域我们称之为单元,我们做好一系列的单元,就可以用它拼出我们需要的形状,处理复杂的几何问题。

在有限元软件中,我们将常用的1D、2D、3D单元构成单元库,需要什么调用什么。

在建筑结构中,这种思想就是单元+组装的方式,建筑用的构件就是杆单元、梁单元还有板单元,我们根据实际情况,就可以组装成满足我们实际复杂几何形状要求的试函数。
这就是我们有限元非常重要的一个基础,由基本构件来构建复杂的对象.
关于有限元的思想,其实在一百多年前就有了,一个是从工程方面,主要是工程师根据工实际得到启发,用直觉的方式构造试函数;另一种是数学家主要从求解微方及试函数如何控制误差这个角度发展有限元。随着各位科学的研究和工业的应用,有限元软件也逐渐发展了起来,成为了工程仿真计算必不可少的工具。

总之呢,时代技术的积累必然会造就美好的世界。





