❆ 模型加载
✦ 启动软件,通过文件-载入-选择上一篇章《Star CCM+案例:移动参考系-旋转风扇》中创建的fan_mrf.sim文件并打开; 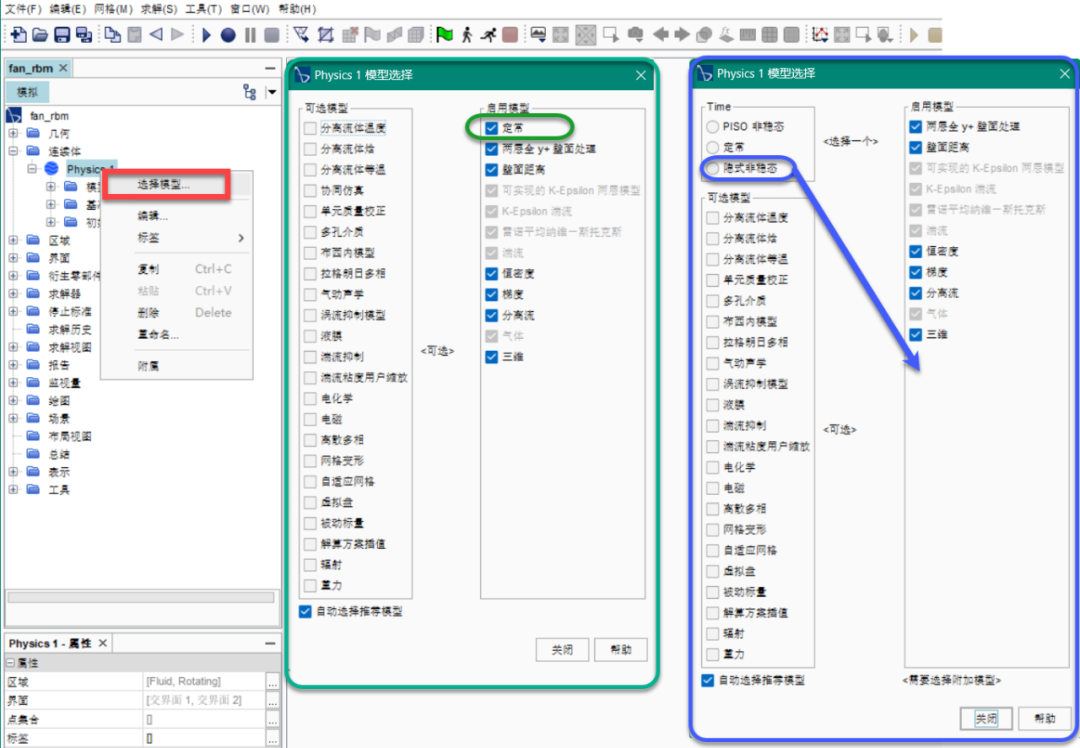
❂_对于先前设置的物理连续体Physics 1进行更改_ ✦ 通过左侧结构树-连续体-Physics 1-右键-选择模型-禁用模型框中的定常(即取消勾选);
✦ 在左侧Time框中-选择隐式非稳态;
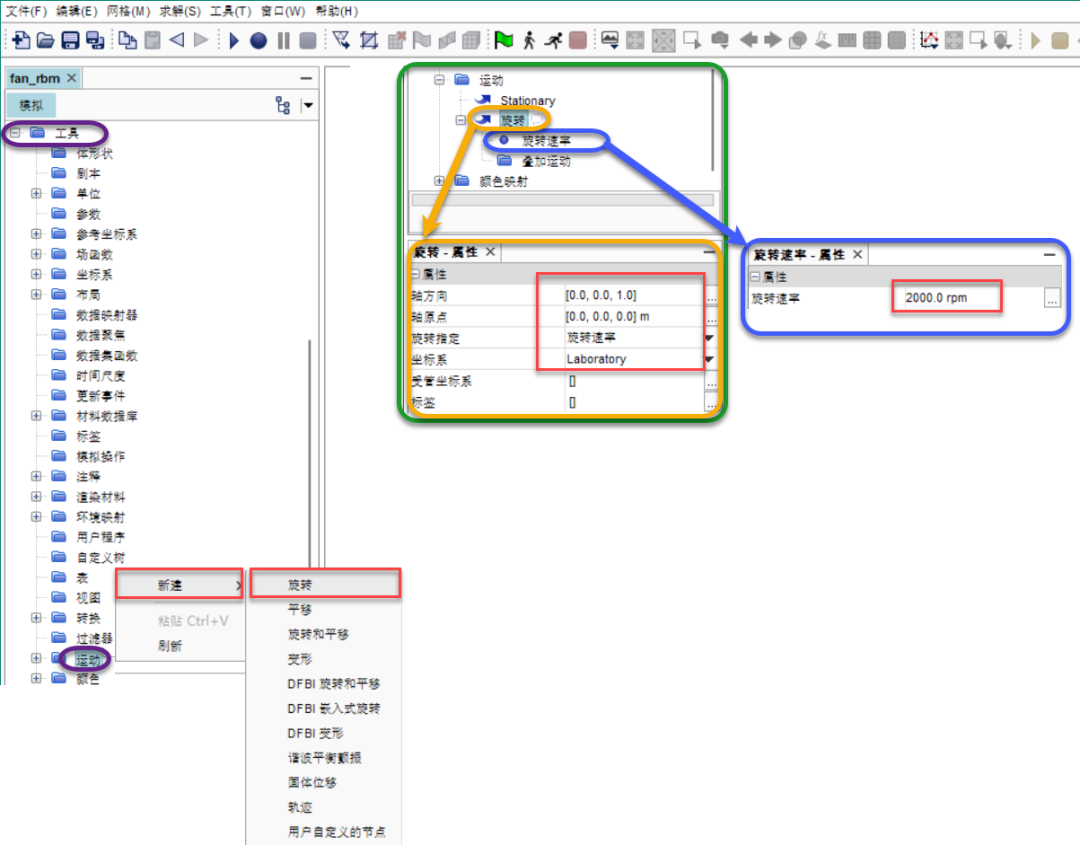
❂_通过左侧结构树-工具-运动-右键-旋转-新建一个运动并参照上图设置_
✦ 设置轴方向为[0,0,1],依据仍然是右手定则判定方向;
✦ 轴原点保持默认[0,0,0]即可,因为其适用于本模型;
✦ 旋转指定选项设置为旋转速率;
✦ 设置旋转速率为2000rpm;
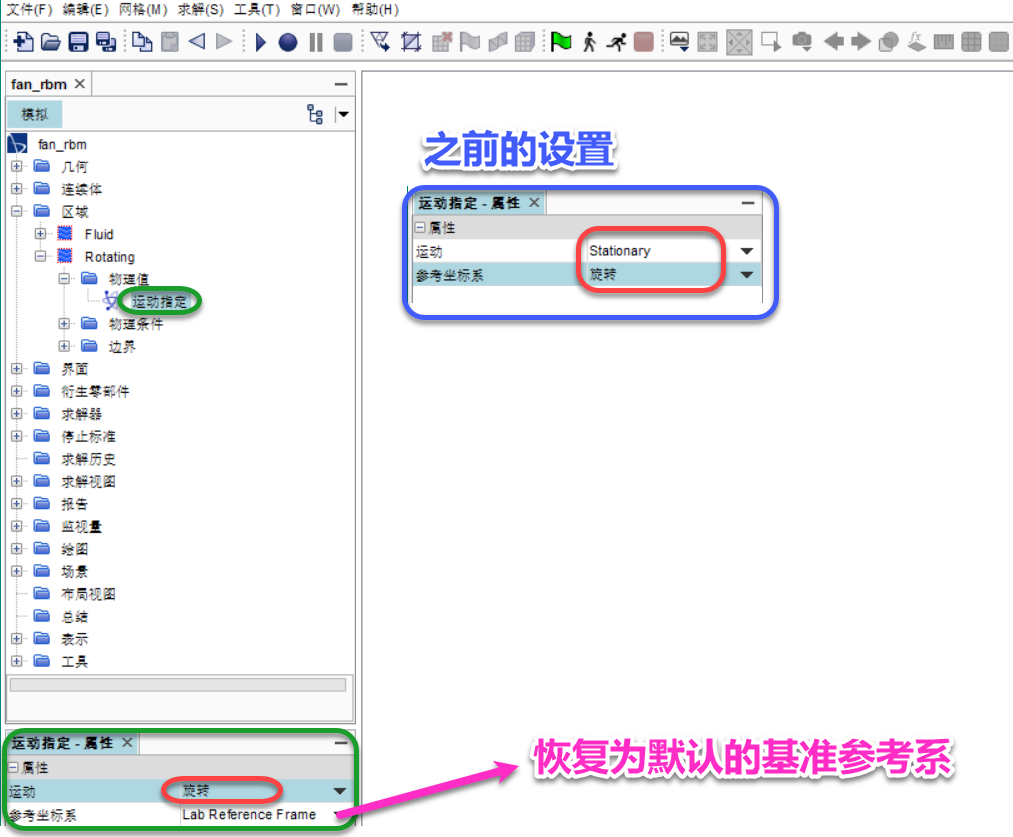
❂_通过左侧结构树-区域-Rotating-物理值-运动指定-在运动框选择之前创建的名为旋转的运动;
✦ 选择此运动后,参考坐标系属性会自动恢复到默认的基准参考系。
❆ 设置求解器参数和停止条件
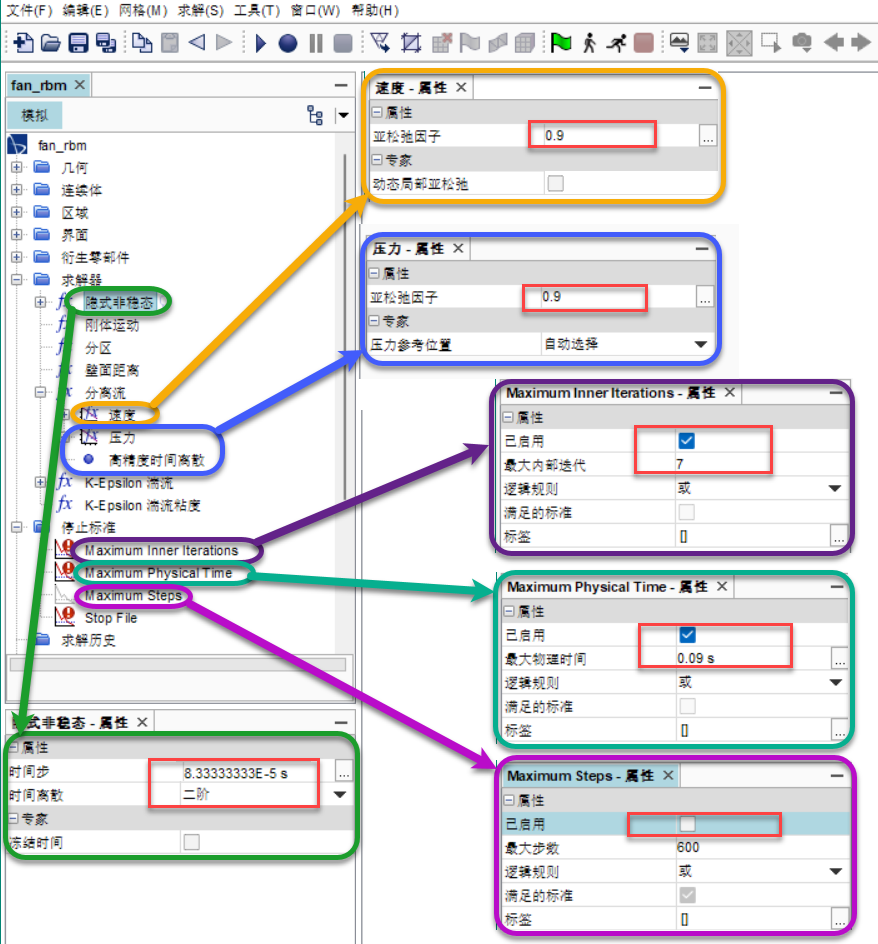
✦ 本案例的叶片旋转速度为2000rpm,即每分钟2000转,即每完成一次完整的旋转需要0.03s; ✦ 通常情况下,建议使用每时间步旋转1度这一标准,即本案例的时间步大小为0.03s/360=8.33333E-5s; ✦ 通过左侧结构树-求解器-分离流-速度-设置其亚松弛因子为0.9; ✦ 通过左侧结构树-求解器-分离流-压力-设置其亚松弛因子为0.9; ❂_通过左侧结构树-停止标准-进行停止条件相关设置_ ✦ 出于演示目的,本案例仅求解三个循环,即叶片完整旋转3圈(0.09s),通过左侧结构树-停止标准-Maximum Physical Time-设置最大物理时间为0.09s; ✦ 关于最大内部迭代,如果该值过低,求解不能在一个时间步内收敛,如果此值过高,则完成求解需要很长时间,本案例设置为7; ✦ 通过左侧结构树-停止标准-Maximum inner Interations-设置最大内部迭代为7; ✦ 通过左侧结构树-停止标准-Maximum Steps-取消勾选已启用选项栏-即禁用最大步数停止条件; ❆ 监视求解
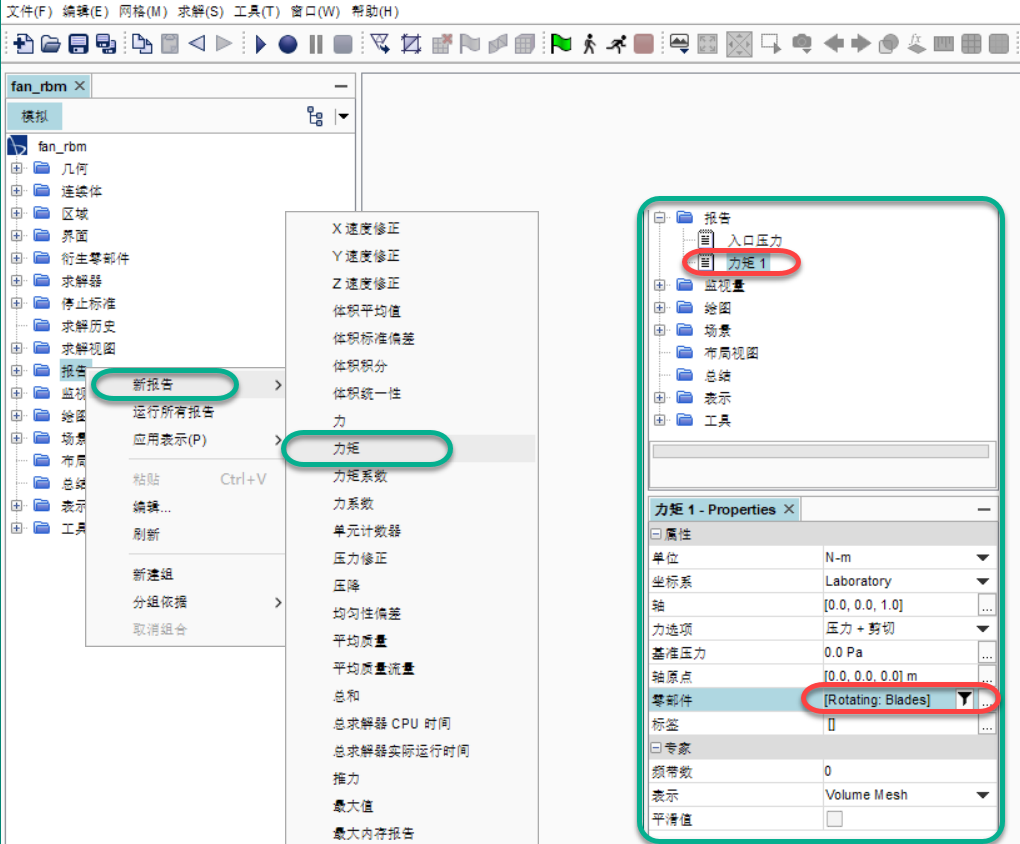
❂_通过左侧结构树-报告-新建一个报告用以表达叶片的力矩信息; ✦ 通过-报告-右键-新报告-力矩-新建一个报告;
✦ 选中刚创建的力矩报告,在其属性框-零部件栏-选择旋转域的叶片(即Rotating:Blades)边界; ✦ 选中该力矩报告-右键-根据报告创建监视器及绘图; ✦ 一个名称为力矩 1 Monitor的新节点出现在监视器节点下方。 ✦ 一个名称为力矩 1 Monitor 绘图的新节点同时出现在绘图节点下方。 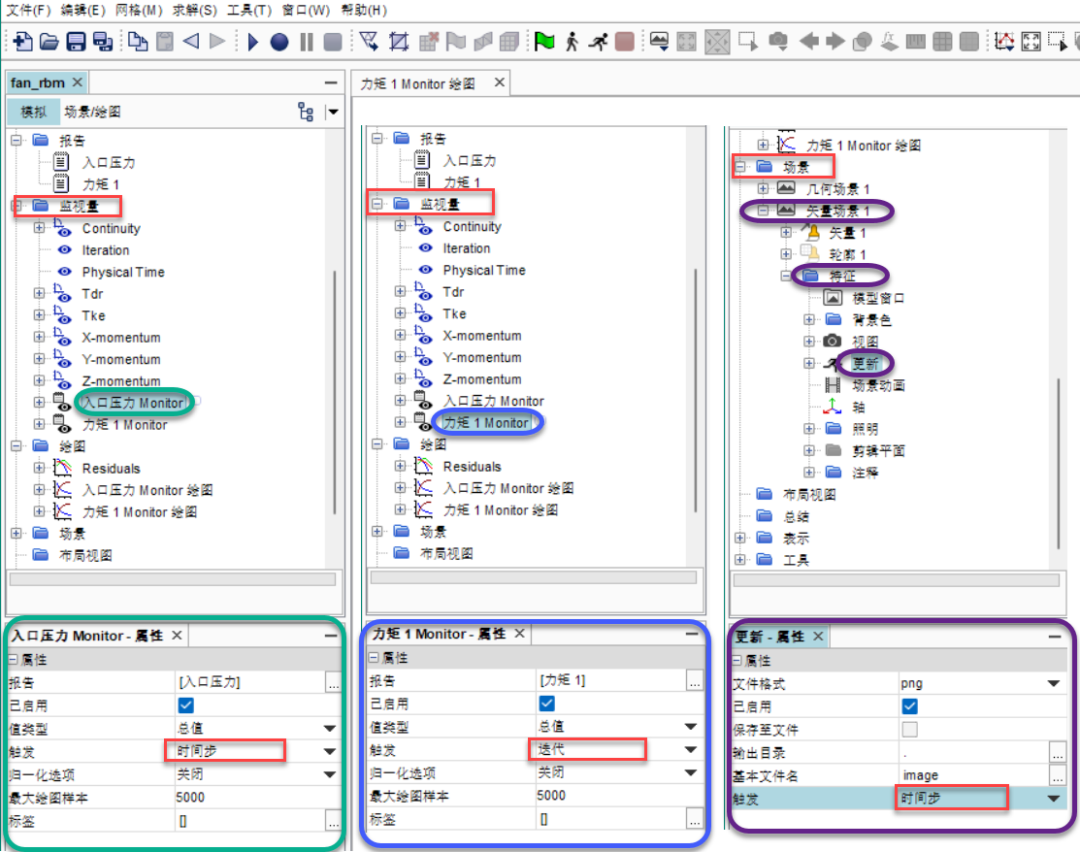
✦ 通过左侧结构树-监视量-选择入口压力 Monitor-并将其属性栏触发节点设置为时间步; ✦ 通过左侧结构树-监视量-选择力矩 1 Monitor-并将其属性栏触发节点设置为迭代; ✦ 通过左侧结构树-场景-选择矢量场景 1-特征-更新-并将其属性栏触发节点设置为时间步; ✦ 力矩的触发节点设置为迭代,可在时间步期间监视此力矩(即监视每个时间步内不同迭代次数的力矩),可提供用于时间步内收敛检查的数据; ✦ 但对于非稳态情况下的大多数绘图而言,更为有用的方法是通过报告每个时间步(而非每次迭代)的量值来查看求解进度,比如本案例的压力报告和矢量仅需要查看每个时间步的数据即可,用以评估求解进度,对于时间步内的迭代并不关心; 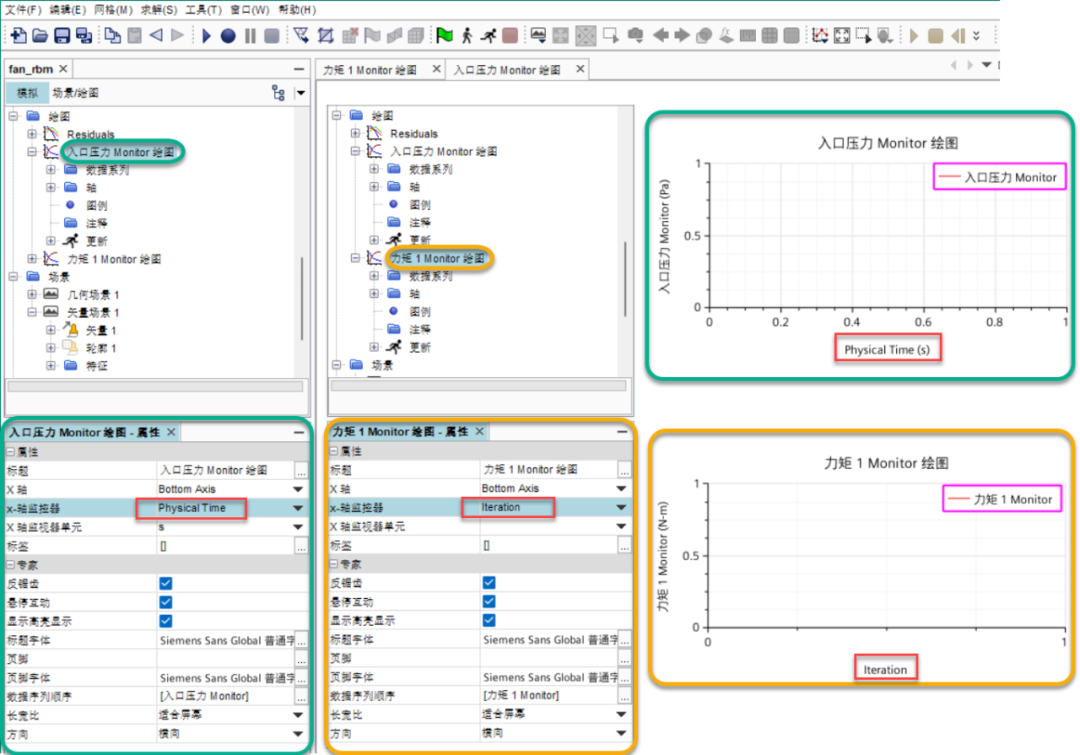
✦ 通过左侧结构树-绘图-选择入口压力 Monitor 绘图-将其属性栏x-轴监视器节点设置为Physical Time; ✦ 通过左侧结构树-绘图-选择力矩 1 Monitor 绘图-将其属性栏x-轴监视器节点设置为Iteration; ✦ 通过在图形区域检查两个绘图的X轴信息,以保证修改完成,使监视与绘图相对应,力矩报告触发节点为迭代,绘图X轴为迭代次数,压力报告触发节点为时间步,绘图X轴为物理时间; ❆ 初始化&模拟
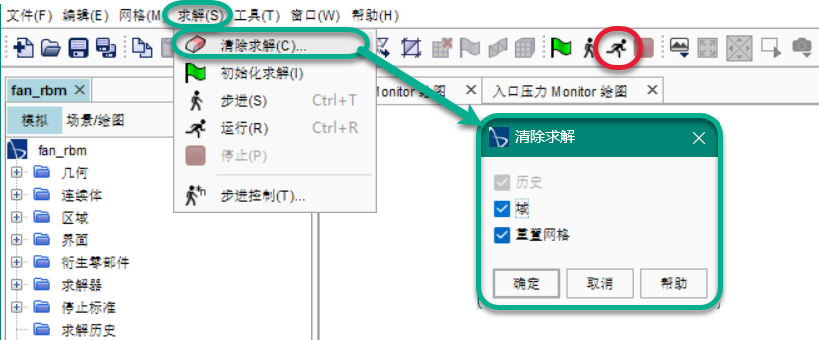
✦ 通过顶部菜单栏-求解-清除求解-清除之前的求解数据; ✦ 通过顶部工具栏-运行(Ctrl+R)-开始模拟; ✦ 此时将自动创建“残差”屏幕,并在其中显示求解器进度; 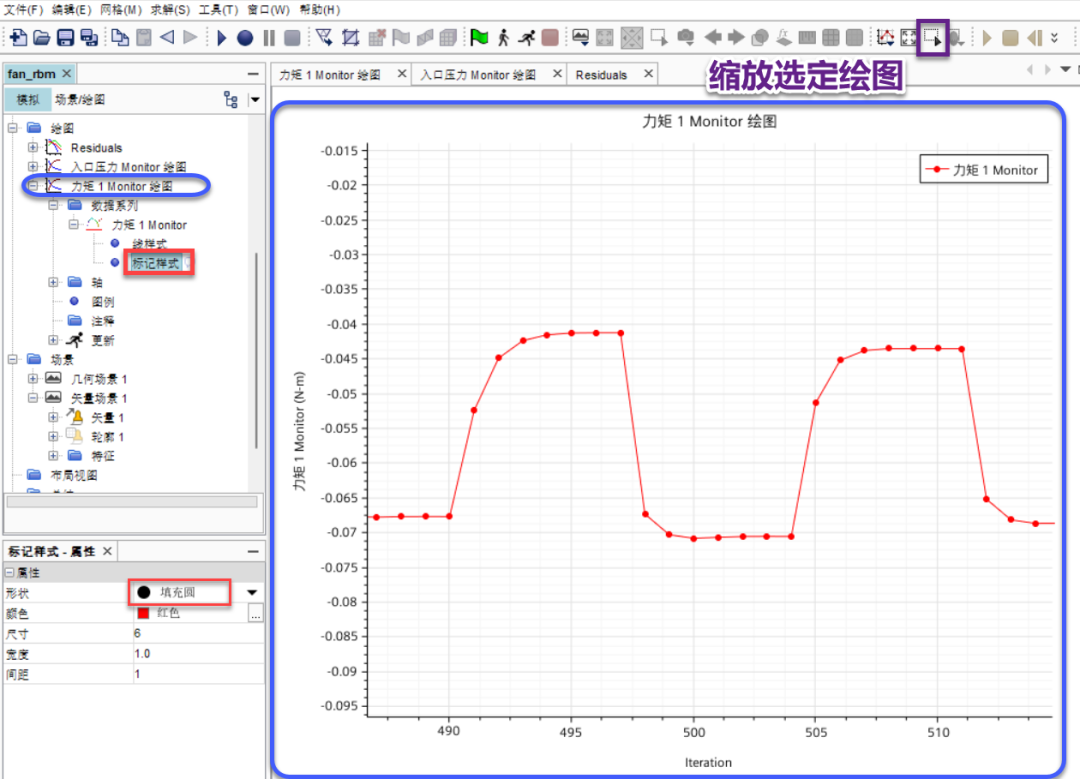
✦ 通过左侧结构树-绘图-选择力矩 1 Monitor 绘图-数据系列-力矩 1 Monitor-标记样式-将属性栏形状节点设置为填充圆,即可改变右侧绘图样式,使数据点以填充圆形式展示; ✦ 可通过滚动鼠标滚轮或顶部工具栏的缩放选定绘图进行局部绘图曲线的放大查看; ✦ 上述分布明确说明在每个时间步内求解的确已收敛,在每个时间步中分布呈平稳状态。 ❆ 后处理
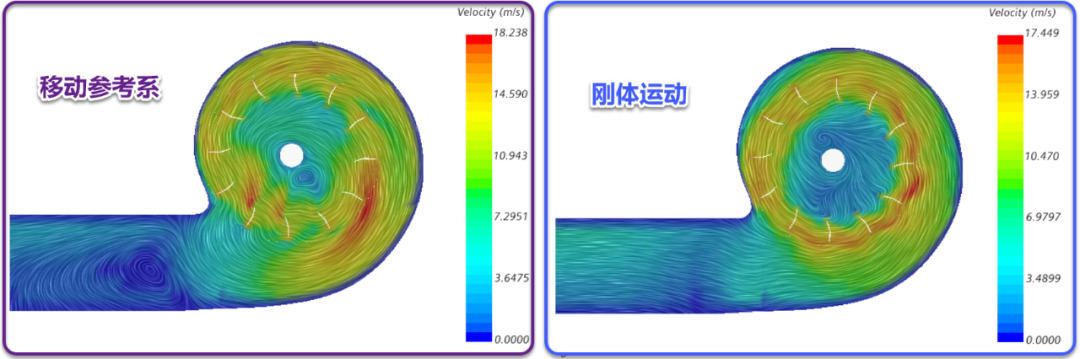
✦ 入口压力绘图的Y轴使用了大比例缩放,导致难以评估求解循环期间的入口压力变化,因此需要更新绘图; 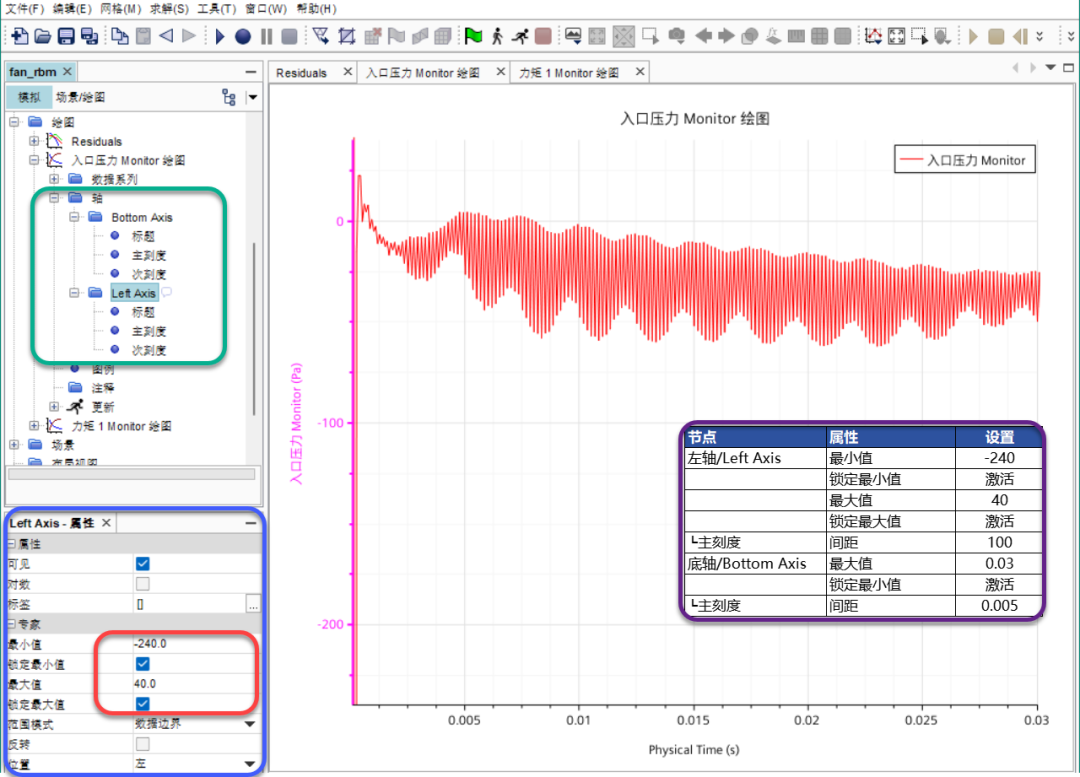
✦ 通过左侧结构树-绘图-选择入口压力 Monitor 绘图-轴节点,参照图中信息进行设置,显示如上; ✦ 入口压力以0.0025s(即1/12转)的周期振荡,与预期相同,因为本案例模型叶片数量为12片; ✦ 随着时间推移,这些振荡的幅值在流体循环稳定下来的过程中趋于固定; 
















