多功能碳纤维复合材料-3
本文摘要(由ai生成):
这篇文档主要讨论了一种新型碳纤维复合材料的机械和物理性能、在拉伸和压缩中的 PECT 效应、短路电流测量以及能量收集。研究发现该材料具有 100GPa 的纵向弹性模量和 1460kg/cm3 的平均密度。在拉伸和压缩中,PECT 效应会导致电压变化,短路电流测量显示电流与应变呈线性关系。能量收集方面,串联电阻器可在 0.18%应变差下产生约 69nW/g 的可用功率。文档还介绍了使用恒电位仪测量电流变化的实验装置和结果,得出基于活性 CF 电极质量,测得的最大功率约为 18nW/g,填充系数约为 26%的结论。
4.结果
4.1. 层压板的机械和物理性能
所得的层压板具有 100GPa 的纵向(纤维方向) 弹 性模量,该弹性模量是通过层压板的弯曲和拉伸测试获 得的。弯曲试验的载荷-位移曲线和拉伸试验的应力-应 变曲线的示例如图 2 所示。

图 2. 层压板的机械测试。
(a) CF 复合材料层压板三点弯曲的示例力-位移曲线
(b) CF 复合材料层板拉伸试验的示例应力-应变曲线。
使用组成成分的体积分数和密度来推导复合材料 层压板的密度。CF 的密度为 1.8g/cm3,分离器的密度为 1.435g/cm3, SBE 的密度为 1.23g/cm3 。 CF 层中 CF 与 SBE 的平均体积分数为 49%,而分离器层中分离器与 SBE 之间的体积分数为 45%。这给出了 1460kg/cm3 的 层压板的平均密度。相比之下, 典型的 CF 单向预浸料 的模量在 130 – 180 GPa 范围内,密度约为1600 kg/cm3, 而铝的模量为 69 GPa, 密度为 2700 kg/ cm3。在对样品进行灌封和抛光后, 使用显微镜获得 CF 的 32μm 和分 离器的 20μm 的层厚度(见图 1f)。应该注意的是,厚度 的变化导致不同样品的计算机械性能的变化。
4.2. PECT 在拉伸和压缩中的作用
活化后,将层压板从袋状电池袋中取出, 并包裹在 低密度聚丙烯薄层(厚度≈15μm)中,以防止 SBE 的液 相蒸发。将层压板夹在一端以形成悬臂, 将两个集电器 连接到恒电位仪以施加和测量电流和电压。已知恒定曲 率的两部分 3D 打印夹具用于使悬臂沿纤维方向机械变 形(见图 1e)。在释放变形 25 秒之前,用夹具将变形保 持在适当位置约 25 秒。在最终变形保持约 120 秒之前, 重复进行四次。应变状态如图 3a 所示, 一层为压缩状态, 另一层为拉伸状态,振幅相等。在变形状态下, 纤 维方向上的应变通过层压板厚度线性变化。这里,每个 CF 层中的平均应变变化(Δε33)用于表示变形应变状态 (见图 S6)。图 3b 显示了上 CF 电极被重复变形到 30 mm 的半径,对应于 Δε33=0.09%的平均拉伸应变变化。 在变形时,观察到电势从稳态明显上升,与 Li 金属对电 极相比, 幅度约为 0.52±0.14 mV。图 3c 显示了相同变 形过程中较低的 CF 层,但 Δε33=−0.09%。从稳态开始, 电势明显下降,与 Li 相比,幅度约为 0.49±0.13 mV 。 电压的变化与施加变形的速度一样快。压缩 PECT 效应因此在大小上与拉伸 PECT 效应相等,但在符号上相反。
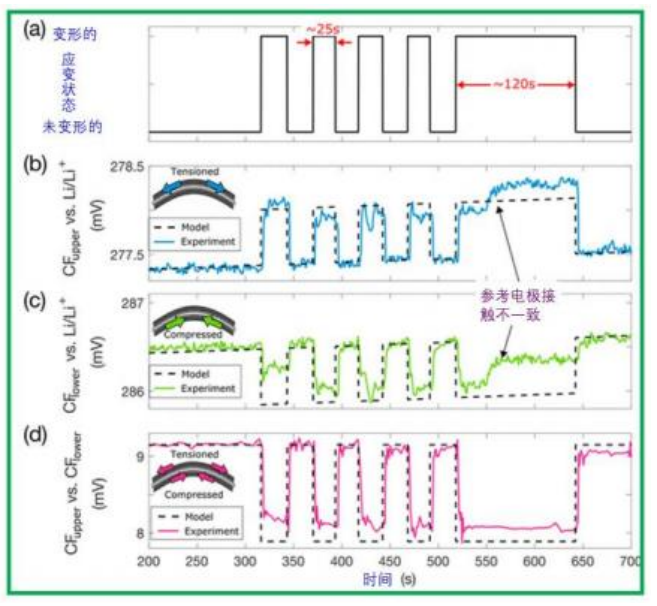
图 3. PECT 测量。
(a) 悬臂循环弯曲过程中的应变状态。
(b) (b ,c)悬臂的上 CF 层和下 CF 层分别相对于锂金属 参比电极的电压。在测量过程中观察到参比电极中大 约 0.2mV 的漂移。这是在使用梯度约为 4×10-4 mV/s 的线性增加的初始电压进行建模时考虑到的。
(c) (d)悬臂的两个 CF 层之间的电压差。虚线是理论预 测。
在图 3b,c 中可以看到电势的微小变化, 特别是在 较长的变形过程中。这被认为是由与锂金属参比电极的 接触不一致引起的。
图 3d 显示了在测量两个 CF 层之间的电势时的相 同测试。电压变化约为 1mV。这等于两个独立测量的电 极电势的大小之和。这里, 在没有参考电极的情况下, 电压在变形时看起来保持更加一致,并且电压没有返回 到稳定状态的趋势。因此,施加弯曲变形有效地使可获 得的电压变化加倍。这种效应使得能够在没有寄生成分 的情况下测量材料内的弯曲应变。
对于 0.09%的应变, 预测的电压变化与 Li/Li+的关 系为 0.63mV,如图 3b、c 中的虚线所示,这与实验观察 结果非常一致。当应变至±0.09%时,这导致两个 CF 层 之间的电压差为 1.26 mV,这也与图 3d 中的实验数据非 常一致。预测的变化略高于实验观测值, 这种差异被认 为是由模型简化引起的,例如,施加的边界条件和使用 的材料数据。
测试了直接拉伸中的 PECT 效应,以验证使用平均 应变来表示弯曲变形的假设。这是使用先前描述的方法 进行测量的。使用拉伸试验机将 0.11%的循环拉伸应变 施加到锂化 CF 束上,并测量 PECT 响应。电位变化的 幅度为 0.52 mV,这与之前的工作一致。这表明,使用 夹具施加的平均应变可以与使用直接拉伸应变施加的 平均应力进行比较。
4.3. 短路电流测量
通过防止层压板变形时的电流流动, PECT 效应产 生开路电位(OCP) 的变化。相反, 通过外部电路连接 两个 CF 电极并施加 0V 电位, 当层压板变形时,电流 将流动,称为短路电流(SCC)。OCP 和 SCC 分别给出 了施加应变时可用电压和电流变化的上限。电化学和机 械系统的耦合性质使得能量收集成为可能。
测量两个 CF 层之间的 OCP 和 SCC 的各种应用平 均应变差,由 2|Δε33|给出。例如,一层张紧至 0.09%应 变,另一层压缩至-0.09%应变,应变差变为0.18%。使用 四种不同的夹具施加一定范围的应变,使应变差等于 0.04 、0.06 、0.08 和 0.18%。通过翻转夹具来施加向上和 向下弯曲。对于 OCP 测量,将两个 CF 电极连接到恒电 位仪,并且在测量电压时不允许电流流动。对于 SCC, 使用恒电位仪将 CF 层之间的电压保持在0V,并测量电 流。悬臂首先在向下弯曲时变形, 然后在向上弯曲中变 形,施加应变约 10 秒, 其间间隔 10 秒。
图 4a 显示了在向上和向下弯曲的施加应变范围内 的 OCP 响应。 OCP 随着施加应变的增加而增加,当从 向下弯曲变为向上弯曲时符号相反。图 4b 显示了每个 施加应变的平均 OCP 变化幅度。误差条表示 OCP 在非 应变和应变状态下的标准偏差的总和。OCP 响应与应变 呈线性关系, 在 0.18%的应变差下达到约 1.5mV 的最大值。当将应变方向从向上弯曲反转为向下弯曲时,OCP 响应的符号从正变为负,尽管响应的幅度基本相同。因 此,OCP 响应是材料中平均应变水平以及弯曲状态的直 接测量。
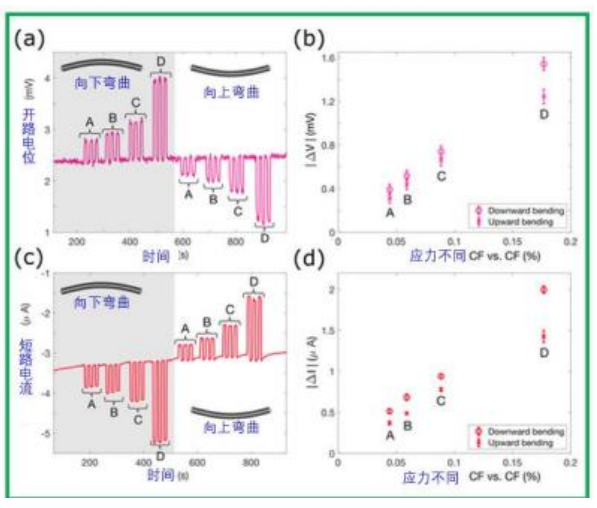
图 4. OCP 和 SCC 在不同弯曲曲率下的响应。
(a) 两个 CF 层之间的 OCP,用于在向上和向下弯曲中变 化
(b) 的应变差。
(c) 对于不同的应变差异,两个 CF 层之间的 OCP 响应的 平均幅度。两个 CF 层之间的SCC,用于向上和向下弯 曲中的不同应变差异。
(d) 对于不同的应变差异,两个 CF 层之间的 SCC 响应 的平均幅度。这里使用的 CF 层叠悬臂的有效长度为
42 毫米,宽度为 15 毫米,总质量为 78.5 毫克。有效 CF 电极质量为 43.6 毫克。
图 4c 显示了施加应变后的 SCC 响应,而图 4d 显 示了平均 SCC 变化的幅度,误差条表示未应变和应变状 态下 SCC 标准偏差的总和。SCC 响应的大小与应变呈线性关系,在应变差为 0.18%的情况下,最大值约为 2μa 。 SCC 遵循与 OCP 相同的模式,当从向上弯曲到向下弯 曲时,响应变化符号。对于向上弯曲, 电流变化的幅度 略低。这可能是由于 CF 层之间的残余负电流较小。这 在电化学系统中产生了离子分布梯度,这将略微放大更 负的响应, 并略微抑制更正的响应。
4.4. 能量收集
OCP 和 SCC 的测量给出了可用功率的理论上限, 两者的乘积给出了理想的可用功率。这是类似能量采集 器经常报告的功率。在这种情况下,基于活性 CF 电极 质量,可用的最大理想功率约为 69 nW/g。然而,由于 测量 SCC 时没有电势差,测量 OCP 时没有电流,因此 不会产生功率。为了测量实际可用功率,有必要在电路 中具有已知的电气负载。
普雷梅斯贝格(Preimesberger)等人报告的方法用于在 电路中串联连接各种电阻器,如图 5a 所示。使用了 10 、 100 、 1000 和 7000Ω 的电阻器。使用了最高的可用施加 应变,对应于 0.18%的应变差。使用恒电位仪在 CF 层 之间施加 0V,并测量复合悬臂偏转时的电流变化。使用 欧姆定律计算电阻器两端的相应电压变化。电压变化和 电流的乘积就是输出功率。
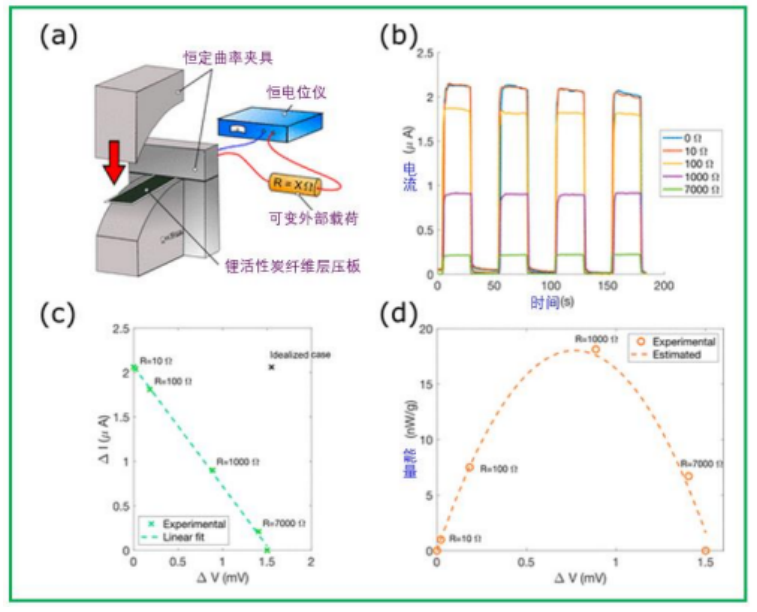
图 5. 能量收集结果。
(a) 测量可用于能量收集的功率的实验装置。在测量 电流变化的同时,将不同的外部电负载与 CF 层 压板和恒电位仪串联连接。
(b) 弯曲过程中两个 CF 层之间的SCC,应变差为 0.18%。
(c) 在各种外部电气负载和测量响应的线性拟合的情况 下弯曲过程中的电流-电压分布。
(d) 在各种外部电负载和 43.6mg 的活性 CF 电极质 量的情况下用于能量收集的重量功率分布。
图 5b 显示了施加应变时的电流分布,外部电阻增 加导致电流响应降低。图 5c 显示了由此产生的电流-电 压曲线。正如预期的那样, 对于小扰动, 电流和电压之 间的关系是线性的。线性曲线拟合如图 5c 所示。然后可以计算功率,如图 5d 所示。理论功率可以通过对图 5c 中关于电压的线性曲线拟合进行积分来计算。基于活性 CF 电极质量, 测得的最大功率约为 18nW/g。因此, 填 充系数约为 26%,与其他地方报道的类似, 填充系数定 义为理想功率与最大可用功率之间的比率。使用 1000Ω 外部电阻器获得最大功率,该电阻器与使用电阻抗谱法 发现的 860ΩCF 层之间的内部电阻大致匹配。这与最大 功率转移定理以及先前的发现一致。




