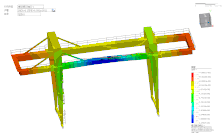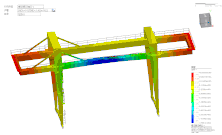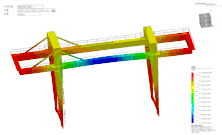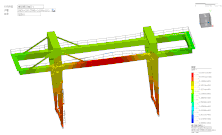
MeshFree|模具吊装仿真分析

静强度、静刚度
假定条件


区分材料是塑性的还是脆性的。最常用的是,用试验拉断后的伸长率来区分,如果伸长率大于5%,就是塑性材料。对于大多数的塑性材料,伸长率都会超过10%。
塑性材料的失效理论有:最大剪应力理论(Treasca理论)以及最大畸变能理论(Von Mises理论)。
脆性材料的失效理论包括:最大拉应力理论、最大伸长线应变理论。
最大剪(切)应力理论(第三强度理论)
认为最大剪应力是引起材料屈服破坏的主要因素。只要有一点的最大剪应力τmax达到单向拉伸屈服剪应力τS时,材料就在该处出现明显塑性变形或屈服。

式中:
σ1和σ3分别为材料在复杂应力状态下的最大主应力和最小主应力
[σ]为材料的许用应力
此理论对于塑性材料的屈服破坏能够得到较为满意的解释。并能解释材料在三向均压下不发生塑性变形或断裂的事实。
需注意:
最大畸变能密度理论(第四强度理论)

最大拉应力理论(第一强度理论)

1.该理论只考虑σ1,而没有考虑σ2、σ3的影响

此理论对于一拉一压的二向应力状态、且压应力较大的脆性材料的断裂较符合,如铸铁受拉压时比第一强度理论更接近实际情况。
适用材料
石料或砼等材料在轴向压缩试验时,如端部无摩擦,试件将沿垂直于压力的方向发生断裂,这一方向就是最大伸长线应变的方向,这与第二强度理论的结果相近
需注意:
应变由应力引起,拉应变并不一定由拉应力引起。
轴向压缩时、或二向压应力状态时、二向拉应力状态时、或三向压应力状态时不适合用该理论
小结:
在常温和静载的条件下,脆性材料多发生脆性断裂,故通常采用第一、第二强度理论;塑性材料多发生塑性屈服,故应采用第三、第四强度理论
无论是塑性材料或脆性材料:在三向拉应力接近相等的情况下,都以断裂的形式破坏,所以应采用最大拉应力理论
无论是塑性材料或脆性材料:在三向压应力接近相等的情况下,都引起塑性变形,所以应采用第三或第四强度理论
示例-以MeshFree
第一步:导入几何(最新版支持格式及版本)

对于模具常用的UG-CAD,MeshFree支持11-NX2306版本的*.prt,为了提高导入CAD速度,建议可以导出x_t parasolid格式。

可调用MeshFree自带材料库,也可以自定义

第三步:定义边界和荷载
接触边界
MeshFree支持焊接、滑动、一般接触



压边圈