【技术贴】通过优化声学包降低汽车噪声
通过优化声学包降低汽车噪声
Michaël THIVANT1; Olivier MINCK2
1:VIBRATEC, 28 chemin du petit bois, Ecully, France
2:MICRODB, 28 chemin du petit bois, Ecully, France
摘要:在即将实施的欧盟法规中,对汽车的通过噪声(Pass-By-Noise)有了更加严格的要求。汽车制造商需要进一步优化声学包来满足这一要求。ECONBEX是一个法国资助的研究项目,旨在一定的附加质量和成本前提下,将车辆动力总成对噪声的贡献量降低5~7dB。本研究计划中汇集了OEM,原材料供应商,声学包制造商,大学研究团队和专业技术顾问,从而实现了材料、设计、测试和计算方法的创新。本文将重点介绍一种用于优化声学包的新方法,这种方法是基于3D准确定位并量化声源的前提下,在能量边界元方法的基础上,来计算噪声的传播。得到的噪声强度分布图能够直观的显示噪声的主要传播路径,以及吸声和隔声材料的最佳布置位置。在此基础上,设计声学包时可以同时考虑声源和声学包的空间和频谱特性,从而可以得到效果最优的声学包。根据噪声源的频谱特性来选择最佳吸声和隔声材料,同时能够满足工业实施的要求。最终,测试和计算结果是令人满意的。
1. 绪论
欧盟新法规中对汽车的通过噪声有了更加严格的要求,同时还要求逐年降低汽车的噪声水平。这部法规要求在未来8年内,将汽车的通过噪声降低4dB。按照这个标准,市面上97%的汽车将不满足这个要求。本文研究是基于2014设立的Econbex项目,这个项目由法国政府及包括OEM,RJP,Lsover 和研究院所在内的9个研究机构组成。项目的目标旨在满足附加质量和成本要求的前提下,通过优化发动机的声学包来降低发动机对通过噪声的贡献量,以适应欧盟新法规的要求。本文的思路是将动力总成视为3D噪声声源,并导入至仿真软件中来预测声学包的有效性以及外部噪声的量级。
文章的第一部分将介绍一种测试动力总成3D声场的有效方法,并通过实际测试来验证后处理方法的有效性。文章的第二部分,介绍了一种车辆声学模型。计算得到的车辆通过噪声与实验结果有较好的一致性。并基于此提出了一种优化的声学包方案。
2. 动力总成噪声特性
第一部分的详细内容见文献1。
2.1 测试方法
2.1.1 patch 测试
使用麦克风阵列测量雷诺汽车动力系统周围的3D声辐射,并且测试得到的声压可以直接映射在声学模型上,因而测试结果可以在仿真计算时继续使用。
对于使用声阵列进行声场测量,需要保证不同通道之间的信号是同步的,因而最好的方法是在发动机周围布置大量麦克风,并通过单次测量来获取声场数据。但这一方法需要数百个频率范围在6khz以上的麦克成,而这需要一笔很大的费用。
鉴于此,我们只用了Patch测量方法,因为这种方法只需要使用一个麦克风阵列(54通道)。实验过程中需要将阵列布置在被测试对象的周围。在此之前,还需要借助交叉谱矩阵(CSM)来使各个通道完全同步。计算CSM矩阵时,我们借助参考麦克风,并借助文献2中的参考相位法来获得。
互谱矩阵(SMM)可以通过下式求得:

其中SHRM代表参考传感器与麦克风阵列互谱的Hermitian矩阵;S-1RR代表参考互谱矩阵的伪逆矩阵;
各个通道间信号同步的程度强烈依赖于SRR平方矩阵的逆矩阵的质量。此处,我们使用的方法是将矩阵进行分解,并使用上式求出各个分量矩阵的虚拟S_MM矩阵。并通过使衡量测量得到互谱矩阵与计算得到的互谱矩阵之间的偏差最小,来确定需要的分量矩阵的个数。最后通过每个通道与参考通道之间的互谱矩阵来修正全局互谱矩阵。
2.1.2 阵列定位系统
Patch方法需要围绕发动机来布置传感器的位置,因而需要一个准确的方法来确定传感器的布置位置。Vibratec 公司的MicordB团队使用了基于飞行时间的定位探针,来确保定位精度在1mm以内。这种方法便于测试结果由阵列所使用的坐标系向声源网格使用的坐标系的快速转换。
2.1.3 传递函数评估
一旦几何形状确定后,就需要来确网格上的节点与麦克风之间的声学传递函数。大多数声学成像设备都是基于自由场假设的。这一假设是不考虑测试对象引起的散射和反射行为。以发动机声源定位为例,这一假设经常容易造成严重的声源成像误差和虚假声压幅值的现象。如果是在消声室内进行声源测试,且声源确实在测试面上,自由场假设下的测试结果是基本满足要求的。
第二种方法是测量传递函数,但这需要覆盖6hkz的频带,且需要测试5000个节点上的传递函数。这一过程需要耗费大量的时间,而且需要处理大量的数据。
第三种方法是使用经由MicrodB实测验证过的FEM或者BEM软件[3]。然而这一方法也异常麻烦。使用这一方法时需要将网格上的数据与麦克风上的数据进行传递,还需要计算高频段的结果。计算完成后还需要将仿真结果再导入到测试系统中,以便于做后处理。
第四种方法则是将预估传递函数的算法集成到测试软件中。这一方法是有T.Mayueres博士在MocrodB时构建的[4]。这种方法是基于适用于传递函数计算的等效源建模(ESM)方法得来的[5],该方法有以下两个假设:
声辐射源是刚性的(网格法向速度0);
Sommerfeld辐射条件
这种方法在文献1中通过与刚性球体的理论解与发动机上实测结果进行对比得到了验证。EMS方法被认为是一种便捷准确的方法。这一方法的优点是可以使用同一套网格来进行传递函数仿真计算以及阵列测试数据的后处理,因而省去了繁琐的数据导入导出操作。
2.2 后处理
2.2.1 广义声学全息成像
通过传递函数和声阵列同步测试结果得到传播模型后,可以得到动力总成网格上的声压幅值和主要声源的位置。现有文献中有很多方法介绍通过阵列测试结果来重构声源。比如可以通过平面波分解法或是使用球谐函数分解赫姆霍兹方程最小二乘法等等。现有研究表明,上述方法可以借助概率统计方法在简单2D结构[5]或者复杂3D箱体结构[6]上进行使用。而广义声全息技术正是结合概率统计方法和上述的传递函数构建而来的。关于噪声和未知声源的概率统计方法的更多介绍可参见文献5,6.使用这种方法可以获得满足最小残差和从能量角度最稳定的声源在网格上的分布结果。进而,可以对以下表达式进行简化:

其中
H是传递函数矩阵,描述了声源从网格结点向麦克风的传递特性。传递函数矩阵由ESM方法得到;
q是网格节点上点源复振幅的未知量;
p是由重新同步的CSM矩阵计算得到的复压力向量;
λ是使用贝叶斯方法计算的正则化参数[6];
从而,我们得到了著名的Tikhonov方程:
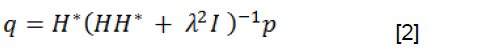
一旦点源的体积速度能够得到,就能够完成向3D网格的映射,以得到每个网格单元上的声功率。
2.3 在动力总成上的应用
2.3.1 搭建测试平台
我们将雷诺汽车的动力总成安装在CRITT M2A全消声室中,并选择了几组特定运行工况。测试系统由适用于不同发动机转速的设备及不同传动比传动系统,来模拟车辆的最大通过噪声。实验中对发动机在不同转速和传动比下,以及空转下的噪声水平进行了测试。图1中显示了阵列的5个测试位置(相当于270个麦克风),并选取其中的8个作为参考通道。
由于仿真计算中动力总成的网格不包含支撑结构,因而在实际测试中支撑结构都使用声学材料进行覆盖,以避免造成声反射。

图1 发动机测试台,发动机网格模型及测试阵列位置
2.3.2 测试结果
图2为最大转矩下,齿轮箱位于3档,选定发动机转速下,2Khz处的声学全息图示例。其中红圈区域为发动机油泵。

图2 2kHz处,发动机不同表明的声强分布
为了验证使用阵列测试结果计算得到的声功率结果的准确性,我们使用声强探头对发动机在低怠速,一定扭矩下的噪声水平进行了测试。使用声强探头进行测试时,遵从了ISO9614-2标准,对每个面进行扫描测试。图2显示了测试结果与计算结果的对比,两组结果的偏差在2dB的偏差范围内。
这种3D声学全息成像技术具有以下优点:
结果分析更加简单,结果可以直接反应在网格节点上,而不需要与2D面全息图进行对比;
可以直接在网格上选择子区域,并计算子区域的辐射声功率。

图3 声强探头测试结果(蓝线)与计算结果(橘黄色线)的对比
通过以下步骤,就可以将动力总成噪声声场的结果导入到仿真软件中用于计算动力总成装配到汽车上之后的噪声辐射特性,并用于优化声学包。
3. 车辆声学模型
在此,我们建立了边界元模型,用于计算噪声源从动力总成向测试通过噪声的传感器的传播。模型中通过面单元来表示声源,吸收和反射表面。模型的求解是基于文献11中的能量边界元法。计算的目的是为了获取动力总成对通过噪声的贡献量,进而提出优化声学包的方案[11]。
3.1 车体网格
在此,我们建立了车体和环境的边界元网格。由于求解方法是基于功率平衡原理,因而不考虑声波之间的干扰,也就不受波长标准的限制。在此只需要关注声源的分布以及材料属性即可。
动力总成的网格与仿真计算声源特性时使用的网格相同。此处,我们建立一个立方体远场边界,边界网格的大小为1平方米,以便于计算声源的指向性和声功率。7.5m处设置有接收点,以对比仿真结果与实际位置处麦克风测量得到的声压值。
地面同样进行了网格划分,以考虑地面对声波反射的影响。车体以外的地面并没有进行网格处理,这部分区域对接收点处声压的影响通过对接收点处的声压值进行修正来考虑在内。
此外,我们只对影响到声源向测点麦克风传播的部件进行了网格处理。
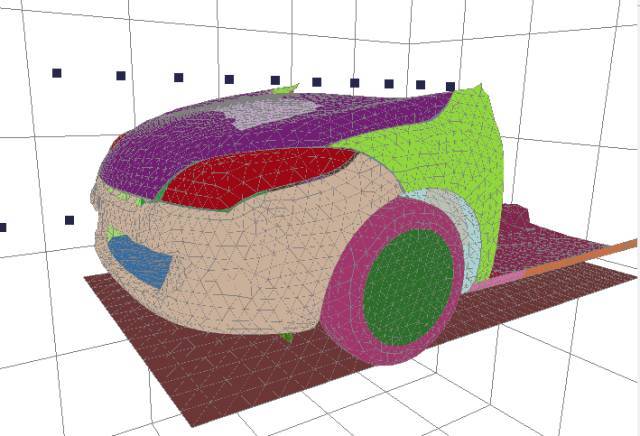
图4 车体、地面、远场网格模型
3.2 材料设置
网格设置完成后,对不同的网格区块设置对应的材料属性。声学包的位置如图5所示,图6中显示车体、轮胎和地面。

图5 右图:标准声学包模型;左图:吸声系数和传递系数

图 6 车体及地面的吸声系数和传递系数
3.3 声源设置
首先,将每个网格节点上的功率谱导出;然后,将其作为声源导入到Sonor软件中。
此外,我们选择噪声最大的工况(全负荷,第三级齿轮转速为1900rpm)来计算动力总成对噪声的贡献量,并优化声学包。
动力总成的噪声谱以1/3倍频的形式加载到仿真计算模型中。
3.4 求解计算
求解计算的理论背景参见文献7,此处我们对其做简要介绍。
3.4.1 模型假设
声波被认为是不相干的,实际声波之间的干扰被忽略。这一假设对高频,宽频带,传播环境复杂的声源是合适的。
用辐射功率来描述噪声源。声功率均匀分布在声源表面,并在各个方向上自由传播;
每个网格节点上的入射场是扩散的
边界对声波的吸收、反射和传递是扩散的(随机发生),并通过下式中的能量系数来描述:
如果节点i接收到其它节点向其传递的功率Wincident(i),该节点将会吸收一定的能量,吸收系数为αi:

节点对声波的反射用下式来表示,ri为反射系数:

功率从k面向i面的传递播关系用下式来表示,其中τik为Diffues场中传递系数:

由能量守恒可知,αi,ri,τik满足以下关系:

3.4.2 视角因数计算
不同边界单元上的能量交换取决于单元之间的“视角因数(view factors)”。这个系数只和几何形状有关(单元面积,起点,两个单元之间的障碍物)。当两个单元之间没有障碍物时,视角因数可以通过解析解求得。
当两个单元之间存在障碍物时,就需要借助Hemicube方法来对视角因数进行计算。
3.4.3 求解边界元问题
为了得到待求解的系统方程,需要对每个边界元单列列出能量平衡方程。对于声学问题,单元i辐射的声功率等于反射、传递和源功率的总和:

反射和传递功率与入射功率的关系如式4和式5所示:
第i个元素的入射功率Wincident(i)等于其他各元素的辐射功率乘以视角因数的和;

由式4,5,7可得:

这样就可得到包含n个未知量(各个单元上的辐射功率)的n个 方程(在n个边界元单元上)。
并可以通过稀疏矩阵SuperLU方法求解上述方程组。
3.5 结果分析
3.5.1 辐射强度云图
首先,我们可以得到各个网格单元辐射的功率。
在这个结果的基础上,我们也可以得到各单元辐射强度的云图。从接收点处来看辐射云图,就可以很直观的看到声压的主要传播路径。从图7可以看出,大部分辐射声源在发动机机舱的右侧区域,通过动力总成下声学包旁边的孔传出,并经由地面反射传递到右侧接收器。

图7 辐射强度 右视图和下视图
3.5.2 入射强度图
使用式8可以计算得到入射功率,并绘制出入射强度云图。这一结果能够指导我们在最佳的位置铺放吸声材料。

图 8 入射强度云图
3.5.3 传播和反射强度云图
通过式4和5可以计算得到各个单元的透射和反射功率强度,从而可以画出透射和辐射功率强度云图。图9显示了发动机舱下的传播和辐射功率强度云图。
可以看出,图7中的辐射功率主要是由于声波反射引起的,而不是由于透射。这一结果表明:声学包的透射系数是足够高的,从而通过声学包底部的吸声系数来降低声学包与地面之间的混响能够起到更好的隔声效果。

图 9 发动机底板上的反射(上)和传递强度(下)
3.5.4 功率平衡
为了量化声学包的入射、反射和传递功率,吸声材料位置处的入射功率或是可能向舱内传递噪声的面板上的入射功率,我们对功率平衡做了进一步计算。
3.5.5 声压云图和频谱
通过公式10,我们可以得到接收点上的压力云图以及频谱图,如下图10和11所示:

其中,p2 (j)是第j个点上的压力平方值,W(i)是第i个单元面的辐射功率,VFij是第i个面与第j个点的立体角。

图10 动力总成对7.5m位置接收点上噪声的贡献。右侧接收点上声压值相对较高

图 11 最大通过噪声工况下,7.5接收点处的声压值
通过在特定的工况中开启响应的源项,就能够获得发动机不同表面对噪声的贡献量。这一结果为使用声学包降低发动机噪声,确定发动机的主要振动源以及在发动机噪声的传播路径上安装声学包提供了有效的指导。
3.6 验证
通过测试结果来对计算结果进行验证。
3.6.1 全局辐射声功率
图12 显示了在低怠速工况下车辆的噪声声功率。灰色曲线表示使用发动机测试平台上测试得到的动力总成的声场数据,上述汽车模型,以及标准声学包模型得到的声功率结果。橙色曲线代表根据ISO标准,在混响室中通过测试声压级得到的声功率结果。仿真计算结果相比实测结果低1.4dB,但考虑到以下因素,这是一个相当好的计算结果:
声源表征方法的不确定性;
车辆声功率测量的不确定性;
发动机在实验台以及在真实车辆上的装配差异;
进气和排气噪声的影响;
计算模型的不确定性;

图 12怠速条件下声功率测试值与计算值的对比

图13 声学包插入损失测试值与计算值对比
图13显示了两组不同声学包的插入损失差异,其中灰线是计算结果,橙色线是混响室中测试结果。两条曲线有较好的一致性(偏差在0.3dB)。因而,该模型可以认为在计算声学包插入损失时是准确的。
3.6.2 声压水平
为了比较在通过噪声测试条件下接收点的声压值,我们将车辆安装在半消声室中的传动台上。发动机的转速和齿轮传动比满足PBN(Pass-by Noise)测试总对加速度的要求,此时发动机噪声位于最大水平。由于测试环境的限制,测点与车轴的距离为2m,而不是7m。测试过程中,前轮安装有滚动轮胎,且已经将轮胎转动产生的噪声降低至最小值。由于正常测试时,轮胎在转动测试台上正常滚动的,因而需要从测试结果中剔除由于轮胎滚动产生的噪声,才能得到动力总成贡献的声压级。因为轮胎产生的噪声与动力总成产生的噪声水平在一个量级,使得这一操作又增加了测试的不确定性。
测试完成后,我们将四个麦克风测试得到的声压的平均值与图14得到的理论计算值进行对比。
尽管计算值在低频段段偏高,而在2000-3150Hz偏低,但总的计算结果与实际测试值得偏差只有0.9dB。从而确定,该理论计算方法在仿真计算动力总成对噪声贡献量时是准确的。

图14 PNB测试条件下,测试得到的动力总成声压级与仿真值得对比
3.7 优化声学包
借助仿真计算结果以及在使用声场云图对传递路径的分析,我们提出来四种优化后的声学包设计方案。其中声学效果最好的设计方案如图15所示。这一方案在距离动力总成在7.5m处的侧点上有7dBA的插入损失。目前,我们的合作伙伴正在对这一方案进行详细的研究,以便使其更加具有实用价值。此外,我们还进行了新材料方面的研究。
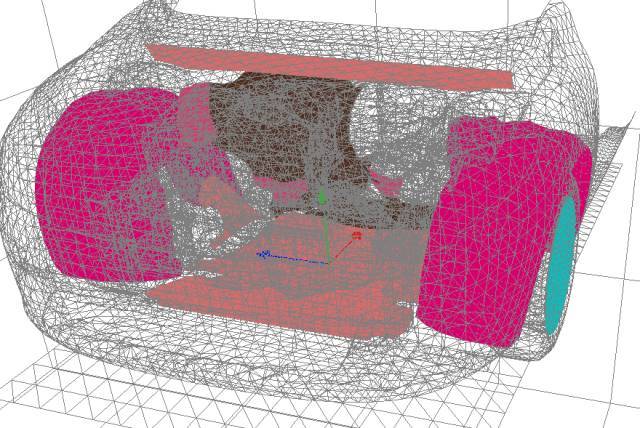
图15 优化后的声学包示意图

图 16 优化后的声学包插入损失仿真值
4. 结论
在欧盟法规即将提高车辆噪声标准的限制下,Vibratec和MicrodB提出了一种在3D边界元网格法基础上计算动力总成噪声水平的方法。在此基础上,将计算结果导入到车体声学模型中,从而可以用于预测车辆的通过噪声并优化声学包设计。实验表明,文章提出的方法与测试结果有较好的一致性,并适用于工业应用。雷诺汽车已经采用了本文研究提出的具有7dB插入损失的新的声学包设计,样车于2016年底下线。
了解方案中使用的工具sonor软件
请联系懿朵科技
参考文献
1. Minck, Olivier & Al. Array based acoustic power measurement, Renault Pass-By Noise. In: Proceeding of NVHG Congresse, Japan; 2016. p. 887-909.
2. Yoon. S.H, Nelson. P.A. A method for the efficient construction of acoustic pressure cross-spectral matrices [J] Journal of sound and vibration, 2000, 233(5): 897-920.
3. Le Magueresse. T, Minck. O. Source localization inside cabin using calculated Green’s function. [J]. Automotive NVH Confort, SIA 2012.
4. Le Magueresse T. “Approche multidimensionnelle du problème d’identification acoustique inverse », PhD Thesis, 2016.
5. Pavic. G. A technique for the computation of sound radiation by vibrating bodies using multipole substitute sources. [J]. Acta Acustica united with Acustica, 2006, 92(1):112-126.
6. Antoni. J. A Bayesian approach to sound source reconstruction: optimal basis, regularization, and focusing. JASA, 2012.
7. M. Thivant, P. Bouvet, A. Cloix and N. Blairon, Boundary Element Energy Method for the acoustic design of vehicles shileds, Proceedings of ISNVH, Graz (2008)
8. A. Le Bot, A vibroacoustic model for high frequency analysis. In Journal of sound and vibration, vol.211, no.4, , p. 537-554 (1998)
10. B. Betgen, M. Thivant, P. Bouvet, A. Cloix and A. Bocquillet, Boundary Element Energy Method for the acoustic prediction of vehicle external and interior noise – Validation on a mock-up and industrial application In Proceedings of DAGA (2011)
11. B. Betgen, M. Thivant, P. Bouvet, A. Cloix and T. Lambert, Boundary Element Energy Method for the acoustic prediction of automotive external noise In Proceedings of DAGA (2013)
来源:懿朵科技