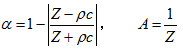电机径向力相位对振动噪声的影响——【电驱动系统NVH系列专题(六)】
本文摘要:(由ai生成)本文研究了电机径向力相位对振动噪声的影响,特别是在三合一或多合一电驱动系统中。通过仿真对比了不同斜极形式的影响,并深入分析了电磁力幅值、相位和声功率。研究发现,径向力相位差对零阶模态共振有显著影响,实际状态与理论值存在明显偏离。文章强调在振动优化时,需综合考虑径向力幅值和相位的影响,并建立合理的目标函数来降噪。懿朵科技提供全方位的NVH解决方案。电机径向力相位对振动噪声的影响方江龙 唐旭 对于三合一或多合一电驱动系统,其常见NVH问题包括两类:低速区由切向激励激发总成弯扭模态引起的弯扭振动;高速区由零阶径向激励与圆柱零阶模态共振引起的径向振动并辐射高频噪声。现有研究表明,转子分段斜极对抑制齿谐波电势、各阶次谐波以及齿槽转矩均有明显作用,因而对改善低速区扭矩问题有显著效果。与此同时,宝马工程师研究对比了不同斜极形式下,零阶激励与结构零阶模态共振峰位置及幅值影响。揭示了径向力相位对零阶共振的影响。在该研究中认为,转子分段后不同段之间磁势的相位差满足如下关系: 并进一步分析不同斜极形式与零阶模态的共振形式及幅值差异。文中结果表明,V型斜极及ZigZag斜极将显著改善零阶模态共振问题。作者近期研究结果表明,以V型斜极为例,假定不同段上零阶激励力幅值相同,相位相差180°,呼吸模态处噪声峰值较无斜极降低量大于10dB。但由于开槽及饱和效应,斜极后不同段上电磁力相位差并不满足上述关系,进而导致型斜极及ZigZag斜极并不能有效改善高速区NVH问题。由此说明应该高速区振动噪声峰值一方面取决于径向电磁力幅值,另一方面不同段上电磁力的相位将对径向振动的幅值产生显著影响。在电驱动系统早期开发或者NVH优化时,为控制高速区径向振动问题,通常对径向电磁力幅值进行控制或优化。但如果忽略了不同段之间径向力相位的影响,有可能导致优化目标不准确,甚至预期降噪效果与实际降噪效果产生严重偏离。本文借助仿真结果,首先对比理想状态下即径向力相位差与斜极角度满足1式条件下,不同斜极形式对振动噪声的影响;其次对比实际状态下不同斜极形式对振动噪声的影响;最后,提取某电磁方案在迭代优化过程中不同段上径向电磁力幅值及相位的变化,借此探讨如何在优化过程中考虑相位对振动响应的影响,进而得到更加准确合理的优化目标。1.零阶结构模态 本文计算中结构前三阶圆柱模态如下图1.1所示,更高阶零阶模态超出了本文分析频段范围,在此不再展示。前三阶零阶模态频率如表1.1所示。 图1.1 零阶圆柱模态振型 表1.1圆柱零阶模态 2.理想状态下电磁力幅值及相位 本文计算中选取某8极48槽电机为研究对象。由表1.1各阶模态圆柱模态频率可以,(48,0)阶电磁力与0-1阶圆柱模态,0-0阶圆柱模态以及0-2阶圆柱模态的共振转速分别为:8250rpm,8510rpm及11755rpm。后续分析(48,0)阶径向电磁力时重点关注以上三个转速区间。 2.1 不同斜极形式下电磁力幅值与相位文中提取电磁力时采用2D电磁模型。忽略端部效应,不同斜极形式电磁力处理方式如下:在无斜极时,认为电磁力在轴向不同截面处相同;线性斜极(连续斜极)时,斜极角度3.75°,电磁力在轴向不同截面处径向电磁力幅值相同,48阶径向力相位从铁心一端到另一端线性增大180°;V型斜极(4段),第一段与第二段转子角度相差3.75度;48阶电磁力在两段转子上幅值相同,相位阶跃180°;ZigZag斜极(6段),各段转子初始角度为1.875-4.375-6.875-3.125-5.625-0.625,48阶径向电磁力在各段上幅值相同,转子各段上径向力相位与第一段的相位差为:143°,286°,71°,214°,-71°。2.1.1 无斜极时电磁力幅值及相位 无斜极时,(48,0)径向电磁力及在1000-12000rpm转速区间上的变化如下图2.1所示: 图2.1 无斜极时(48,0)径向电磁力幅值及相位 2.1.2 线性斜极时电磁力在齿面上的分布 线性斜极时电磁力在齿面上的分布如下图2.2所示: 图2.2 线性斜极时径向电磁力在齿面上的分布 2.1.3 V型斜极时不同段的电磁力幅值与相位 V型斜极时,不同段上(48,0)径向电磁力幅值与相位如下图2.3所示: 图2.3 V型斜极时不同段上电磁力幅值及相位差 2.1.4 ZigZag斜极时不同段的电磁力幅值与相位 ZigZag型斜极时,不同段上(48,0)径向电磁力幅值与相位如下图2.4所示: 图2.4 ZigZag斜极时不同段上电磁力幅值及相位差 2.2不同斜极下48阶等效声功率不同斜极形式下48阶在1000-12000rpm声功率计算结果如下图2.5所示。 图2.5 不同斜极形式下48阶声功率 由上图可以得到以下结论:无斜极时,圆柱(0,0)阶模态被激发,声功率峰值94db;圆柱(0,1)及(0,2)阶模态处无显著峰值;线性斜极时,圆柱(0,1)及(0,2)阶模态被激发,其中(0,1)阶模态处峰值与无斜极(0,0)阶模态处峰值接近,(0,1)阶模态处声功率峰值80db;V行斜极时,圆柱(0,0)及(0,2)及模态被激发,其中(0,2)阶模态处声功率幅值88db,大于(0,0)阶模态处峰值78db;两个共振峰处峰值高度均低于无斜极及线性斜极;ZigZag斜极时,圆柱(0,1)及(0,2)阶模态被激发,其中(0,1)阶模态处峰值高度84db,(0,2)阶模态处峰值高度80db; 两个共振峰处峰值高度均低于无斜极及线性斜极。不同斜极形式下96阶在1000-12000rpm声功率计算结果如下图2.5所示。 图2.6 不同斜极形式下96阶声功率 从图2.6可以看出,不同斜极形式激励起的圆柱模态阶次及峰值均有差异。由于其峰值高度较48阶较低,在此不再赘述。由以上结果可以看出,理想状态下,无论V型斜极或ZigZag斜极,对降低(0,0)阶模态处振动噪声峰值均有显著效果;同时需要关注(0,2)阶模态被激发所产生的新的峰值。3.实际激励下不同斜极形式电磁力幅值、相位及声功率 3.1 不同斜极形式下不同段上径向电磁力幅值及相位对比不同与章节2中电磁力幅值与相位结果,本章节中提取不同斜形式电磁力时,建立多段2D电磁模型,给定不同的转子位置后,通过电磁有限元计算提取不同段上实际径向电磁力的幅值与相位。有限元计算得到4段V行斜极与6段V行斜极下(斜极角度均为3.75°),不同段上的(48,0)径向电磁力的幅值、相位如下图3.1及3.2所示。 图3.1 4段V型时不同段上(48,0)径向电磁力的幅值与相位 图3.2 6段V型时不同段上(48,0)径向电磁力的幅值与相位 由图3.1及3.2可看出,斜极状态下,不同段的电磁力的幅值及相位均存在显著差异,即不满足式(1)条件。将不同段上的电磁力分解加载到定子齿面不同截面位置处,得到1000-12000rpm区间上等效声功率对比结果如下图3.3及3.4所示。 图3.3 48阶等效声功率 图3.4 96阶等效声功率 上图中,sega Noskew及segb NoSkew分别表示单独将第一段与第二段电磁力加载到电机结构上得到的声功率结果;sega V shape表示假定两段上电磁力幅值相同,相位差3.75*h(h表示阶次)时,得到的声功率 结果;Actual V shape表示将两段转子上实际的电磁力相位与幅值分别加载到子齿面不同截面位置处,得到等效声功率。从上图3.3可以看出,加载不同段上V行斜极不同段上真实电磁力的幅值与相位后,48阶共振峰值的位置及高度并未显著降低;其峰值高度与理想V形斜极下存在显著性差异(>10dB)。由此说明,在幅值一定条件下,通过设计斜极角度,改变不同段上的径向力的相位差是降低0阶模态共振的有效手段之一。但由于不同段径向力的实际相位差与理论相位差存在显著差异,导致斜极起不到应有的降噪效果。本文中,重点关注48阶噪声变化趋势,在此不再赘述96阶在不同斜极形式下声功率的变化。 图3.5 4段V行斜极(3.75°)两段上理论相位差与实际相位差 4.迭代过程中不同段上径向力幅值及相位的变化 如上所示,在幅值一定条件下,通过设计斜极角度,改变不同段上的径向力的相位差是降低0阶模态共振的有效手段之一。但由于不同段径向力的实际相位差与理论相位差存在显著差异,导致斜极起不到应有的降噪效果。以某4段V型斜极电磁方案迭代优化中间结果为例,迭代过程中不同段上的电磁力幅值、相位及径向力相位差变化分别如下图4.1,图4.2及图4.3所示。 图4.1 迭代过程中不同段径向电磁力幅值变化 图4.2 迭代过程中不同段径向电磁力相位变化 图4.3 迭代过程中不同段径向电磁力相位差变化 由上图结果可以看出,迭代过程中,电磁力幅值、相位及不同段之间电磁力的相位差均均在较大范围内波动。在对48阶电磁噪声进行优化时,除了可以对电磁力幅值进行优化,也可以对不同段上电磁力的相位进行优化。但通常,在进行电磁力幅值优化时,会影响不同段的相位差;在进行电磁力相位优化时,电磁力幅值同样会发生改变。那么,在同时进行电磁幅值与相位优化时,如何建立幅值、相位与振动噪声响应之间的目标函数是另一个值得探讨的问题。以下图为例,假定不同段上电磁力幅值相同,改变不同段之间径向力的相位差,得到不同相位差下电机48阶辐射声功率如下。 图4.4 不同相位差下(V型4段)48阶声功率 5.总结 (1)径向力相位差能够显著影响零阶模态共振的阶次及幅值高度;(2)实际状态下转子不同段之间径向力的相位差与理论值存在显著偏离,进而极大影响斜极对零阶模态共振的抑制作用;(3)在进行振动优化时,需同时关注径向力幅值及相位对响应的影响,通过建立合理的目标函数,得到更好的降噪效果;(4)在对径向力相位进行优化时需要关注制造误差对相位的敏感程度,如电磁力差对制造误差敏感程度较高,则并不能得到预期的降噪效果。(后续论文中进行阐述)来源:懿朵科技