自紧对厚圆筒压力容器极限性能的影响
摘要
本文探讨了厚壁圆柱压力容器在各行业的广泛应用及其复杂的应力分布问题。文章通过拉梅方程描述其应力状态,并强调了解破坏或爆破压力的重要性。回顾了多位研究者对圆柱压力容器破坏压力的预测和分类工作。介绍了有限元分析软件在弹塑性分析中的应用,验证了单轴材料模型的有效性,并讨论了自增强技术的优势。同时,涉及了材料行为的模拟,研究了残余应力分布,并考虑了Bauschinger效应。最后,讨论了弹性应力和过应变压力的概念,并提出了相关的数学模型和表达式,以助于设计出更安全、高效的设备。

HELLO DECEMBER
概述
厚壁圆柱压力容器在军事、国防、航空航天、核工业和化工行业中有着广泛的应用。与薄壁圆柱压力容器相比,厚壁圆柱的应力分布更加复杂,可以通过拉梅方程来表达。了解这些容器的破坏或爆破压力对评估在工作压力下的安全系数至关重要。破坏理论因材料和几何变化而异,因此无法达到唯一的破坏机制。材料的发展也与其他技术同步进行。因此,还需要发展破坏理论,以便对新开发的材料进行表征。早期研究者如Faupel和Crossland&Bones因提供大量测试数据并补充理论背景而受到高度赞扬。
Marin和Weng除了进行大量实验外,还回顾了几个预测圆柱压力容器破坏压力的公式。Christopher等人对许多用于确定圆柱爆破压力的公式进行了分类和批判性分析。Svensson提供的压力扩展关系引起了人们的关注,关于其不稳定性标准和对爆破压力的预测能力。Brabin等人尝试通过有限元分析(FEA)软件Ansys对金属的弹性-塑性行为进行建模,以找到破坏压力。Güven、Liu等人和Zhu&Leis采用不同的破坏准则评估圆柱压力容器的爆破压力,这些程序是严格的。Nejad等人和Ebrahimi等人分别使用Tresca屈服准则及其线性应变硬化的流动规则分析旋转盘和压力容器。Kadam等人对圆柱压力容器进行了严格的爆破压力分析,并对应变施加了限制。Singh等人基于Hill准则进行了三维材料模型的研究。它提供了较不准确的结果,与各向同性材料模型相比。
HELLO DECEMBER
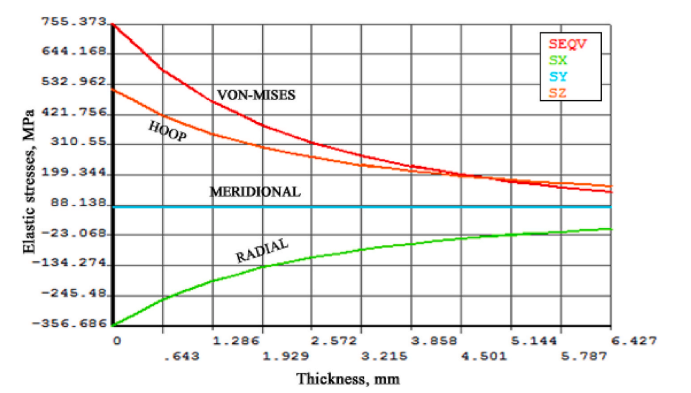
图1.内压作用下一端封闭的厚壁圆筒的弹性应力
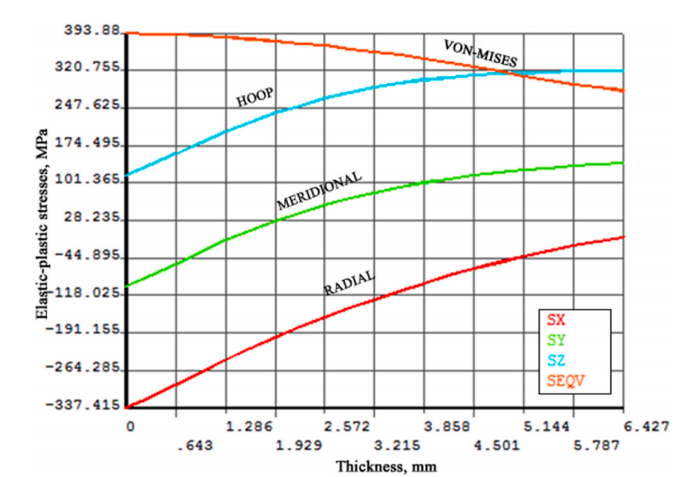
图2.内压作用下封闭端厚壁圆筒的弹塑性应力
本文利用有限元分析软件对单轴材料模型进行了弹塑性分析,验证了单轴材料模型在圆柱形压力容器失效压力评估中的有效性。本文采用了Svensson模型[7]中的失稳判据。失稳判据假定容器的体积为常数,内压对内应变的导数在失效瞬间为零。在失效瞬间,内压对内应变的导数为零。外表面应变与内表面应变接近,材料模型采用Ludwick定律,而本分析中采用的材料模型是与材料试验结果非常吻合的反Ramberg-Osgood关系,但很少被研究人员使用。该方法涉及Von Mises屈服准则,Nejad等人[15]和Mazarei等人[16]也使用了该方法。在本分析中,内表面处的有效应力梯度对于内压为零,并且外表面上的应力接近内壁上的值。此外,一个有趣的现象,称为全球塑性变形(GPD)也被用作一个额外的功能,以确定故障的发生。
自增强是一种在圆柱形压力容器的内径处产生所需深度的压缩性质的残余应力的过程。这是通过将圆柱体加压到预定值然后释放来实现的。残余应力用于提高其使用期间的承载能力。它还有助于增加部件的疲劳寿命[1]。自增强是制造功能梯度材料(FGM)的子类之一。Nejad等人[17]已经回顾了FGM制成的厚壳分析中的关键问题。自增强在枪管中具有特殊优势,具有更高的最大工作压力,这将导致更高的肌肉速度和更大的射程[18]。虽然一方面有利,但不幸的是,由于在圆柱体的外表面上形成拉伸残余应力,自增强处理具有不利的影响。因此,有必要找到最佳的自增强半径和相应的压力。最佳自增强压力如图1所示。内压作用下厚壁封闭圆筒的弹性应力。图2.内压作用下封闭端厚壁圆筒的弹塑性应力。A. Mohan等人的International Journal of Pressure Vessels and Piping 194(2021)104546 3中提出了一种在气缸的内表面上引起最小屈服的方法。Faupel等人[19]提出了一种自增强应力分布的理论关系式,这些关系式由于简化了假设而具有一定的局限性。
在模拟FGM中的材料行为时,Hosseini等人[20],Shishesaz等人[21]和Zarezadeh等人[22]使用应变梯度理论。而Noroozi等人[23]使用非局部应变梯度理论。在处理应力和磁场组合的特殊问题时,Hosseini等人[24],Khoram等人[25]和Barati等人[26]使用了非局部弹性理论。Barati等人[27]在上述组合场中使用了偶应力理论。Zhu & Yang [28]利用Tresca和Mises理论推导出了自紧最佳半径,它们的关系表明,内表面的张力减小,加载时的应力模式有利。包括Majzoobi和Ghomi [29]和Hojjati和Hassani [30]在内的几位作者也推导出了最佳自增强压力和相应的弹性/塑性界面半径的关系。Shim等人[31]进行了实验并模拟了残余应力的分布,包括Bauschinger效应,在高强度钢中。他们发现,当考虑包辛格效应时,孔处的残余应力的大小相对较低。
Huang & Cui [32],Faghidian [33]和Perl & Saley [18]也提出了残余应力的解析表达式,并强调了Bauschinger效应的重要性。受上述研究的启发,在这项工作中,弹塑性有限元分析程序被用来评估自增强产生的残余应力。此外,并将残余应力的应力分量与内压容器的应力分量进行比较,以评价残余应力对爆破压力的影响。


2.压力水平和现象

2.压力水平和现象

HELLO DECEMBER
厚圆柱体中的弹性应力是非常普遍的,并且由下面给出的Lame方程表示[2]。
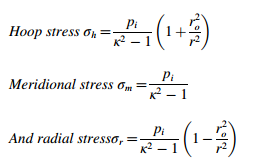
其中,pi,内压; ro,外半径; r,中间半径; κ = ro/ri; ri,内半径。可以注意到,在整个壁厚范围内,径向应力是恒定的,并且是任意点处的环向应力和径向应力的平均值。使用Ansys软件评估的这些弹性变化如图1所示。需要强调的是,在弹塑性条件下的变化将如图2所示。这是进入该主题并研究其行为,特别是对失效行为的动机。弹性破裂压力是应力水平达到内半径ri处的屈服强度(σys)时的压力,由Faupel [3]给出。
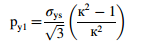
过应变压力对应于压力容器整个厚度达到屈服强度的应力水平[3]。

Faupel [3]假设了圆柱形压力容器失效压力的经验关系,并表示为:
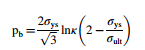
其中σult为材料的极限抗拉强度。Svensson [7]提出了一种假定按照Ludwick定律表现的材料的压力-膨胀关系。Ludwick幂律表示为
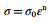
其中,σ是应力,ε是应变,n是应变硬化指数(n =失效时的真应变εu),σ0材料常数表示为
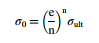
其中,e是自然对数的底。Svensson [7]给出了内表面和外表面应变之间的关系。

其中εi和εo分别是内表面和外表面上的应变。失稳判据将破坏压力定义为内表面应变的一阶导数为零时的压力水平。因此,他推导出了爆破压力的关系,

这个方程可以数值求解;然而,Svensson提供了一个简化的公式,
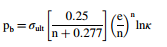
最佳自紧标签的模型之一最佳自增强压力的模型之一的特征在于剪切应力表示为[6],
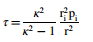
上述方程由方程 1(a-c) 代入得到

产量将发生在内壁表面,当剪切应力达到材料的屈服强度的最大值时。
这导致了在方程(2)中呈现的弹性破裂压力的方程。增加压力后,屈服会继续通过厚度发生。导致在所需半径ri处发生屈服的压力由Christopher等人给出。
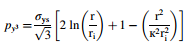
对于r = ro,施加的内部压力对应于方程(3)中表达的过应力或坍塌压力。检查方程(10),可以得出内表面上的残余应力。
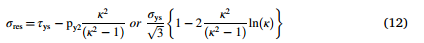
如果在使用中加压后卸载期间应力需要保持弹性,则上述量不应超过相反方向的剪应力。因此,最小直径比由以下表达式计算得出,以使壁完全过度应变。

使用该关系沿着等式(3)并通过代入
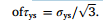
表1(a):圆柱体1-5的材料性质和尺寸。

表1(b) 圆柱体1-5的材料常数(E = 2.06 × 105 MPa,ν = 0.3)。
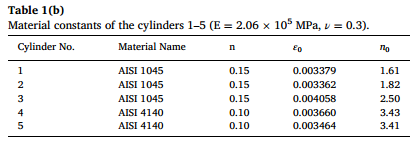
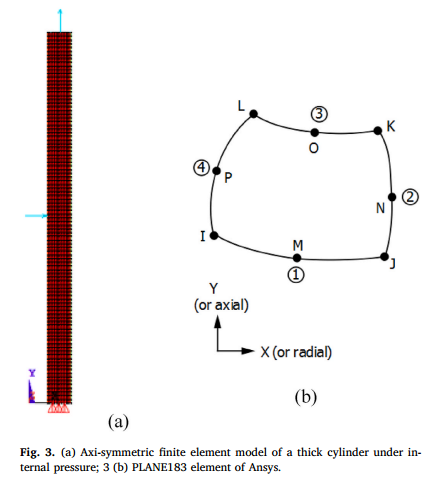
图3。(a) 内压作用下的厚圆筒轴对称有限元模型;3 (b) Ansys的PLANE183单元。图4. 圆筒1的外环向应变。A. Mohan等得到了直径比限制。
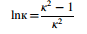
解出的数值κ = 2.218 表明,直径比大于2.218的圆筒在不发生逆向屈服的情况下不能被允许过度应变。因此,不会诱发逆向屈服的最大自动过压压力(py4)可表示为,

值得注意的是,最大自动套压力等于弹性破坏压力的两倍(py4 = 2py1)。上述讨论适用于弹性完全塑性材料,这在制造厚壁圆柱体的钢材中从未成立。为了评估自动套效应,需要进行一种密切逼真地逼近实际材料行为的弹塑性分析。

图4. 圆柱体1的外环应变。A. Mohan等
未完成翻译
本文来源(Effect of autofrettage on the ultimate behavior of thick cylindrical pressure vessels )




