爆炸即为艺术
本文摘要:(由ai生成)
本文探讨了氢气的安全风险及泄爆模拟。通过案例展示了增加泄爆面可显著降低爆炸超压。计算结果显示,设置泄爆后的最高压力远低于封闭情况。文章还指出泄爆模拟边界处理的问题,并提出改进建议。此外,还分享了传爆药冲击起爆数值模拟的相关知识。总之,本文通过模拟展示了泄爆面的重要性,并讨论了相关数值模拟的技术细节,以提升氢气使用的安全性。
艺术是一种转瞬即逝华丽之美,如璀璨的烟火,在爆炸的瞬间迎来华美的高 潮。这不仅是迪达拉的爆炸艺术,也是所有艺术的通用释义。(注:迪达拉-《火影》晓组织一员)

最近机电君痴心爆炸仿真的学习,小小资料分享一下。
简单来说,操作上爆炸就是几个能量方程的写入以及材料模型的设置,最后还有网格的控制。计算时间不超过1ms,爆炸往往在µs级。
数值模拟是进行传爆药冲击起爆过程研究不可或缺的工具。运用软件研究各条件下传爆药冲击起爆及响应细节。
提示,各位道友参考网络参数时候一定要核对一下单位制,并且与软件协调,否则结果不一定,更有可能无法计算,机电君熬了几个通宵被网络上的资料整惨了,所以这里分享的参数也不保证一定可以用,参考需谨慎,结果不保证!
1 传爆药冲击起爆数值模拟反应速率及状态方程
在爆轰波的数值模拟中,选择不同的化学反应率函数,模拟计算出来的爆轰波的发展和传播结果是不同的。常用的有 Arrhenius反应速率方程、Forest Fire模型、Cochran反应速率方程、Lee-Tarver点火增长模型和巴塔洛娃反应速率方程。数值模拟的状态方程包括炸药的状态方程和爆轰产物的状态方程。炸药的状态方程常用HOM状态方程和JWL(Jones-Wilkins-Lee)状态方程。爆轰产物状态方程常用的Abel余容状态方程、Ⅱ-C方程、JWL状态方程和BKW状态方程。
分享模拟计算反应速率方程选择能够一定程度上反映凝聚炸药冲击起爆过程的Lee-Tarver点火增长模型,见式;炸药状态方程和爆轰产物状态方程均选择JWL 状态方程,见式。
Lee-Tarver点火增长模型如下式所示:

λ 是炸药反应度;t 是时间;ρ 是密度;ρ0 是初始密度;p 是压力;I、b、a、x、G、c、d、y、G、e、g、z 是与炸药有关的可调系数。
上式中的第一项,描述点火阶段。点火阶段热点的数量由参数I和x控制,a是炸药临界压缩度。第二项表示孤立热点的反应成长阶段,点火后热点早期的反应增长由G1和d控制。燃烧项压力系数y一般取1,燃耗阶数b和c一般均取为2/3,表示炸药颗粒向内的球形燃烧。第三项描述反应的快速完成阶段,高压下的反应速率由G2和z控制,常数G2可随入射冲击波的压力而改变,pz表示与压力相关的线性燃烧速率,该项认为控制生长过程的因素主要燃烧的压力效应。(不要偷懒,翻翻资料很容易找到这些参数的解释)
JWL 状态方程如下式所示:

式中:A、B、R1、R2、ω为方程参数,可由圆筒试验进行标定;V为相对体积,E为炸药微元的初始内能。
2 施主药柱 RDX 标准输出试验的数值模拟
2.1RDX 标准输出试验装置有限元模型
建立的施主药柱RDX标准输出的试验装置有限元模型如图所示。装置中施主炸药为RDX(GB296-87),密度为1.463g/cm3,药柱总高度为 38.0mm,共分为7个药柱,单个药柱的尺寸为Φ5.0×5.43mm。施主药套筒外径为25.0mm,内径为5.0mm,高为38.0mm,装药壳体材料为45#钢;鉴定块材料为A3钢,在建模模拟时,为节省计算时间,钢鉴定块模型尺寸并未采用Φ110×50mm,由于底边和侧边要设定无反射边界条件,通过反复模拟计算Φ60×30mm 尺寸不影响计算结果,故作为鉴定块模型尺寸。由于模型的对称性,计算采用二分之一模型。计算模型采用中心点起爆方式,省去雷 管元件建模。
计算模型使用Lagrange 单元进行划分,炸药和壳体、鉴定块之间采用 Lagrange/Lagrange 单元之间的Self-interaction 算法,在壳体边界面上施加无反射边界条件,采用 cm-g-µs 建模。
有限元计算模型如图所示。

2.2 材料状态方程及参数
试验的施主炸药RDX密度为1.463g/cm3,采用工程经验公式计算可得输出爆轰压力约为20GPa,要获得其JWL状态方程需做大量圆筒试验确定各个参数,本分享未进行这方面工作。CompB炸药各相关参数,其在密度为 1.630g/cm3,Φ5×38mm 的药柱模型网格尺寸为0.1mm×0.1mm时,经模拟计算可获得爆轰输出压力约为20GPa。因该计算条件CompB 的爆轰输出压力与试验施主RDX药柱用工程经验公式计算得到的爆轰压力极为接近,故建模时采用密度为1.630g/cm3的CompB炸药JWL状态方程代替 RDX 作为主发药柱。此处需要说明,如果其它类已知参数的炸药,能满足符合试验所需输出约为 20GPa 爆轰压力的要求,亦可作为建模时施主炸药材料。当然,如果通过大量试验获得RDX 各状态参数进行模拟更为符合试验情况。
试验装置中,施主炸药的爆轰产物采用JWL状态方程,其形式见上文中分享方程。
CompB 炸药JWL状态方程参数见表所示。

利用Johnson-Cook(J-C)强度模型描述试验装置的钢套筒及鉴定块材料。Johnson-Cook(J-C)强度模型的具体形式为:

该模型能够很好描述金属材料在高应变率、高应变以及高温条件下的应力行为。A、B、n、C、m为材料参数。静态屈服应变,应变硬化指数,应变率相关系数,应变硬化指数,温度相关系数。其他参数由于难打就自行翻阅参考文献吧。
45#钢材料Johnson-Cook强度模型参数

A3钢材料Johnson-Cook强度模型参数

由于Johnson-Cook强度模型本身只描述了偏应力和偏应变的塑性部分,在高应变率、大变形条件下,体积变形部分需要用状态方程来描述。常用的高压固体状态方程包括Bridgman方程、Murnagham方程和 Gruneisen方程。前两者分别描述了等温过程和等熵过程的P-V 关系,它们只是特定条件下的材料各参量间的相互关系。而Gruneisen方程是根据能量守恒定律在着眼于微观的统计力学和宏观的热力学之间建立联系,得到了压力与比容(即体积变形)的关系。它考虑了P,V和其他热力学参量间的关系,是高压条件下最常用的一种内能形式的固体状态方程。45#钢和 A3钢在爆炸冲击作用下实际近似一种绝热熵增的压缩过程,采用Gruneisen状态方程显然更为合理。该方程可表示为:
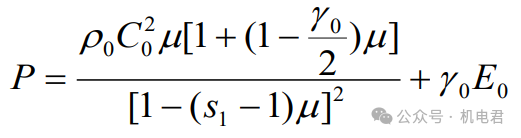

45#钢的Gruneisen状态方程参数

A3钢的Gruneisen状态方程参数

侵彻效果:

2.3 计算结果及分析
在施主药柱中下段的轴向每隔2mm设置1个Gauge观测点,共计9个 Gauge观测点,计算的观测点压力曲线如图 所示。从下图可知,有限元模型中施主药柱轴向爆轰压力约20GPa,与试验采用的密度为1.463g/cm3 的RDX实际输出压力相当,因此计算模型中可以选用密度为1.630g/cm3 的CompB炸药代替RDX药柱。

施主药柱爆轰压力曲线
下图是施主药柱引爆后不同时刻爆轰反应压力云图。施主药柱在t=0µs时刻被雷 管引爆,从图可知,当t=0.642µs时刻,施主炸药已被引爆,并发生反应,产生压力约17.6GPa的冲击波;当t=2.805µs时刻,爆轰反应前沿波已经接近药柱中部,此时爆轰压力约20GPa,且趋于稳定;当 t=5.005µs时刻,爆轰反应前沿波已经到达施主药柱底部,爆轰压力保持在20GPa左右,这与试验RDX施主药柱输出的爆轰压力接近,较为符合试验情况;当t=6.497µs时刻,施主药柱爆轰波已经进入钢鉴定块,此时爆轰压力约5.4GPa。

施主药柱爆轰反应压力云图

钢鉴定块凹坑形成及压力云图
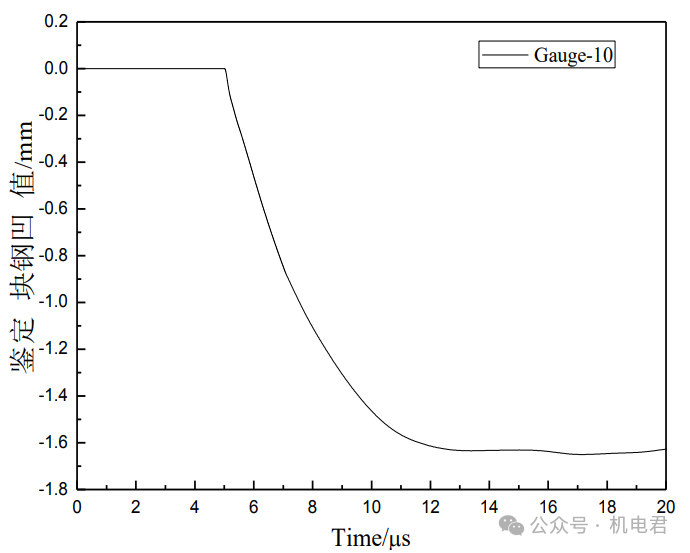
施主药柱侵彻钢鉴定块的凹坑值变化曲线