二维or三维？仁者见仁，智者见智？

7月前浏览1601

浅谈如何用二维轴对称对三维进行简化

（盘管换热器）

作者：极度喜欢上课

一、引言

在现实生活中事物都是三维的，理论上直接采用三维建模进行仿真能得到最接近真实情况的结果，但是在某些情况下，咱们可能只是想初步得到定性的规律不太在意定量的数据，此时简化几何维度能大大减少计算成本（能帮我们解决算得快不快的问题！）。而且三维模型的计算量通常都忒大，对于广大同学来说可能不是都有条件能使用高性能工作站，因此对三维模型进行几何维度上的简化更显得尤为重要（能帮我们解决能不能算的问题！）。

几何维度的简化不是盲目的，有时候简化后的模型所涉及到的方法操作可能比三维模型更加的复杂。本文以COMSOL官网一篇博客《模拟盘管换热器》[1]为例，同大家分享一下如何利用二维轴对称模型对三维模型进行简化。

如图1所示，为盘管换热器。中间螺旋盘管流入热水，四周圆柱流道流入冷空气，热水和冷空气在计算域内进行换热。COMSOL官网博客有详细介绍盘管换热器的背景以及简化的原理，但是并没有给定具体的边界条件，因此本文所展示的盘管换热器模型的各类边界条件均是本人根据仿真实际所进行设置的。

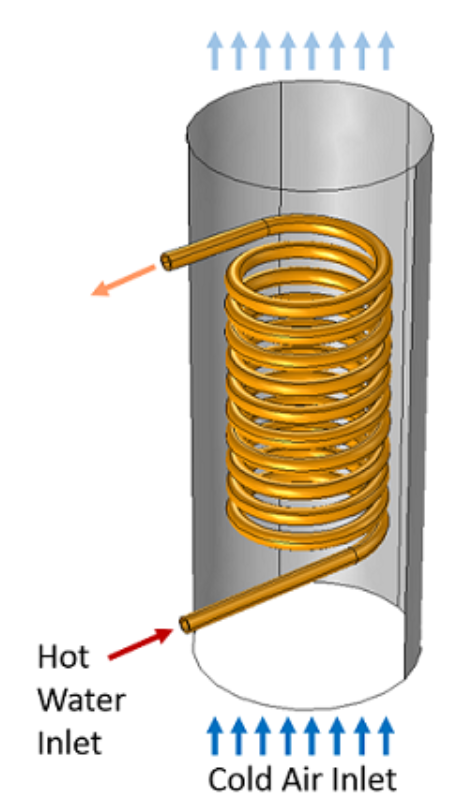
图1（来源COMSOL官网[1]）

二、三维盘管换热器

（一）模型的建立

如图2所示，在三维几何维度下进行建模。盘管总共有13节螺旋，盘管和四周圆柱流道均被0.2毫米厚的铜包裹，盘管内的流体为水，四周圆柱流道的流体为空气。盘管内径为1.6毫米，四周圆柱流道内径为19.6厘米。水的入口速度为0.1米每秒，流入温度为50摄氏度；空气的入口速度为1米每秒，流入温度为25摄氏度。考虑四周圆柱流道管壁对周围环境的自然对流换热，采用“湍流，k-e”进行稳态仿真。

图2

（二）结果分析与讨论

如图3所示，展示了空气（左）和水（右）的温度等值面。温度的分布规律符合实际，空气的入口处温度较低出口处温度较高，水入口处温度较高出口处温度较低。

图3

如图4所示，取一条贯穿盘管和四周圆柱流道的直线来测量温度的变化。空气的出口温度约为302K。

图4

三、二维轴对称盘管换热器

（一）模型的建立

本节的二维轴对称盘管换热器模型是依据上节三维盘管换热器模型进行简化的，单纯的几何维度上的简化并不难，难点在于如何考虑简化之后盘管内水流动的情况以及盘管内水对四周空气的传热。如图5所示，在二维轴对称几何维度下进行建模，其余边界条件与上节三维模型的边界条件一致。

图5

（二）结果分析与讨论

如图6所示，展示了空气的温度等值面（在二维轴对称模型中忽略了水的流动，因此无法给出水的温度等值面）。与三维模型的一致，空气的温度在入口处温度较低出口处温度较高。。

图6

如图7所示，取一条贯穿盘管和四周圆柱流道的直线来测量温度的变化。二维轴对称模型温度整体的变化规律与三维模型一致，特别是空气出口处的温度也是约为302K。。

图7

四、总结

本文利用COMSOL Mutiphysics建模，分别建立“三维盘管换热器模型”和“二维轴对称盘管换热器模型”，两组模型所得到的结果规律基本一致，但是二维轴对称模型的结果和三维模型的结果还是存在一定差异（这里如果要论准确性的话肯定是三维模型更为准确）。这里需要指出的是三维盘管换热器模型的计算时长约为13小时，二维轴对称模型的计算时长约为3分钟，从计算时长来看二维轴对称模型对三维模型是妥妥的降为打击。

至于最终大家是选择“二维盘管换热器”还是“三维盘管换热器”，还得根据实际情况出发，见仁见智。（案例均为本人的原创案例，请大家理性看待。）

来源：COMSOL实例解析