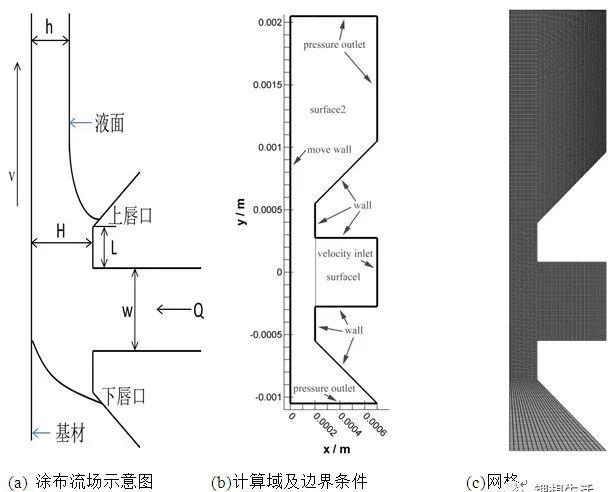
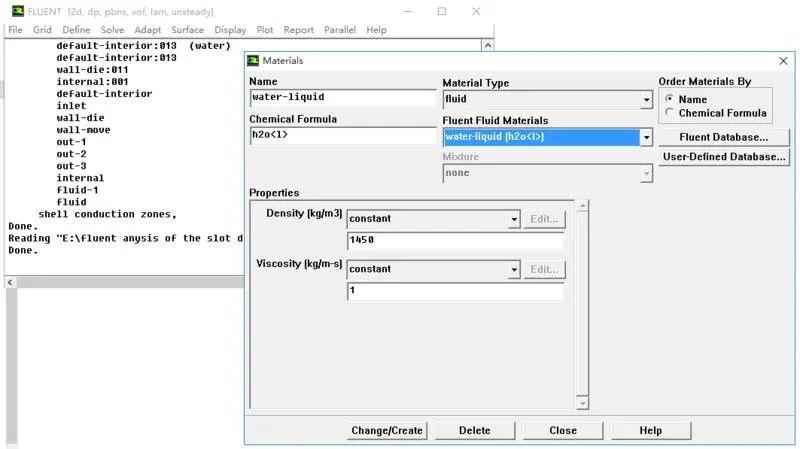
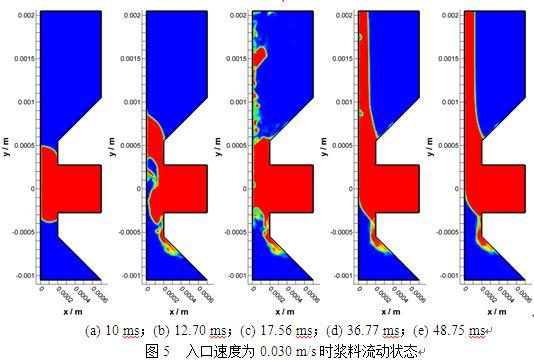
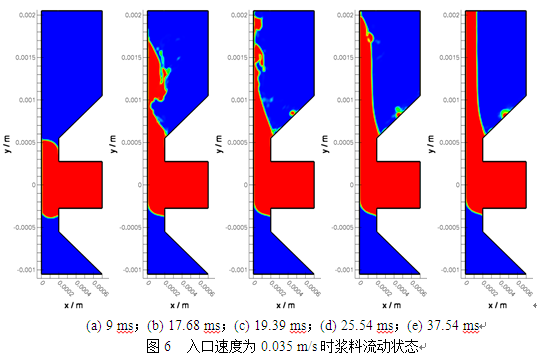
锂离子电池直流内阻分解方法
电池内阻是反映电池性能的重要指标,而测试方法有电化学阻抗谱(EIS)法、单频(1000 Hz)交流阻抗测试、间歇电流中断法、混合脉冲功率表征(HPPC)法,以及开路电压-电池电压(OCV-V)法。通过施加小交流信号测试得到的电阻称为交流内阻ACR,而通过大电流脉冲测试得到的电阻称为直流内阻DCR。相比ACR,DCR测试更贴近真实工作状态,能更直接、准确地反映锂离子电池的性能。此外,DCR不仅会影响电池的极化和发热,还有一些研究人员通过DCR与循环次数的关系来预测电池的健康状况。同时,通过分析循环前后锂离子电池的DCR,可以明确电池的限制因素,高效、快速地指导材料优化。 目前,电池内阻分解主要通过电化学阻抗谱(EIS)来实现,而DCR本质上是指单位电流引起的极化电压。由于电池内部动态过程复杂,很难直接测试单一的极化。因此,有必要通过实验与仿真相结合的方法实现电池DCR的完全分解。 DCR主要以极化的形式呈现,如表1所示。根据动力学过程不同,可分为扩散极化、电化学极化、欧姆极化;根据成分不同,可分为正极液/固相极化、隔膜液相极化、负极液/固相极化和集流体固相极化。 根据以上所述,DCR根据动力学不同分为欧姆内阻(R ohm )、扩散内阻(R diff )和电化学反应内阻(R act )。直流内阻分解步骤如下:第一步,获得直流欧姆内阻。由于直流和交流条件下的欧姆内阻基本相等,因此使用内阻测试仪在5mV、1000Hz条件下测量得到的交流内阻看成直流欧姆内阻(R ohm )。第二步,获得电化学反应内阻和欧姆内阻之和。电化学反应内阻和欧姆内阻的响应时间一般在1秒以内。Ruan等通过建立电化学阻抗谱的高精度多时间尺度模型,在时域上分解了1 s内的阻抗(1sR)情况,当电池处于50%荷电状态时,1sR主要为由电化学反应内阻和欧姆内阻组成,扩散内阻仅占5.02%。因此,我们可以近似认为1sR为电化学反应内阻和欧姆内阻之和。 在每个SOC下,电池以1 C 倍率脉冲间歇放电 1 秒,并休息 5 分钟。电阻通过记录1s内的电压降,再除以电流来获得,记为1sR,为电化学反应内阻(R act )和欧姆内阻(R ohm )之和。 其中V 0 表示不同SOC下的初始电压,V 1 表示1秒内的电压下降。其中I代表放电电流,I=1C倍率。 第三步,获得电池整体直流内阻,再计算扩散内阻。通过GITT方法(每次滴定以0.5C倍率施加电流脉冲6min,随后静置松弛30min)获得电池的开路电压OCV曲线,最终通过OCV-V方法得到电池的整体DCR。计算过程如下,电池极化电压等于开路电压-电池实际电压,电池的整体直流内阻Rtot为极化电压乘以电流,那么扩散内阻为整体内阻减去电化学反应内阻(R act )和欧姆内阻(R ohm ),即Rtot-1sR。这样就将电池直流内阻分解成了欧姆内阻(R ohm )和电化学反应内阻(R act ),以及扩散内阻(R diff )。对于全电池,我们可以采用三电极系统分别获得正负极的电压,将正负极内阻分开。利用上述脉冲1s充放电和OCV-V法得到的1sR和R tot ,即分别可得到正极和负极的扩散内阻。直流内阻分解示例 图1 34145圆柱形三电极电池DCR分解将以上方法应用于34145圆柱形三电极电池,可以获得整个电池、正负极在不同温度和放电倍率下的DCR变化。采用1秒内1C倍率脉冲的方法,获得不同温度、不同SOC下整个电池正负极1sR的变化情况。图1a展示了25°C下1C放电的DCR分解,根据动力学过程,可以看到欧姆内阻和电化学活化内阻在整个放电过程中基本保持不变,维持在大约2.7 mΩ~3.2 mΩ左右。只有在放电末期才增加到2.81 mΩ~7.5 mΩ。电池的总内阻变化趋势主要与扩散内阻有关。电池的总扩散内阻(43.03%)大于活化内阻(31.62%)和欧姆内阻(25.35%),表明扩散过程是速度限制步骤。图1b显示了正极的DCR(DCR-pos)大于负极的DCR(DCR-neg),除了在放电中段。在图1c和1d中,阴极的扩散内阻在90% DOD之前低于1sR,而在放电末期扩散内阻的快速增长导致了整体DCR-pos的增加。而对于阳极,扩散内阻在1sR左右波动。 参考文献:[1] Qin, Q., Li, X., Wang, Z., Guo, J., Yan, G., Peng, W., & Guo, H. (2023). Experimental and simulation study of direct current resistance decomposition in large size cylindrical lithium-ion battery. Electrochimica Acta, 465, 142947.[2]A. Nyman, T.G. Zavalis, R. Elger, M.r. Behm, G.r. Lindbergh,Analysis of the Polarization in a Li-Ion Battery Cell by Numerical Simulations,J. Electrochem. Soc., 157 (2010), p. A1236[3]H. Ruan, B. Sun, J. Jiang, W. Zhang, X. He, X. Su, J. Bian, W. Gao,A modified-electrochemical impedance spectroscopy-based multi-time-scale fractional-order model for lithium-ion batteries,Electrochim. Acta, 394 (2021), Article 139066来源:锂想生活