基于GPU的快速气固流动非解析LBM-DEM方法
摘要:本文提出了一种快速的离散颗粒模拟方法,即非解析LBM-DEM。流体相和颗粒相分别由格子Boltzmann法(LBM)和离散单元法(DEM)完成计算,并采用浸入运动边界法(IMB)实现流固耦合。通过将IMB方法中的额外碰撞项视为力源项并引入等效曳力来修正IMB中的权重函数以施加正确的耦合。此外,在GPU端实现了LBM-DEM以提升计算效率。基于非解析LBM-DEM对三种典型的气固流化进行模拟,均与实验数据吻合较好。同时,基于GPU的LBM-DEM相较于CPU或CPU-GPU异构的CFD-DEM算法,计算速度提升了1 ~ 2个数量级。该方法在分辨率尺度和计算效率上均优于传统的CFD-DEM方法,在流态化和多相流计算中具备广泛应用前景。
引言
颗粒流体系统广泛存在于自然界及工业生产中,如石油催化裂化、循环流化床燃烧、煤气化、流化焙烧和沙尘暴等。传统的双流体模型TFM将流体相和颗粒相均视作连续介质求解,无法获得颗粒的详尽信息;直接数值模拟DNS,令流体网格比固体网格小一个数量级,直接解析颗粒受力并描述每个颗粒周围的详细流场,但其计算量巨大,难以实现对真实的流动现象进行模拟。离散颗粒模拟DPS介于双流体模型和直接数值模拟之间,其不解析颗粒的受力,而是基于曳力方程关联流体和颗粒,不仅可以获得颗粒运动轨迹等局部信息,也可以获得流体的平均流场信息。其采用的流体网格可比颗粒尺寸大一个数量级,能在计算精度和成本之间达到一个平衡,已成为探索实验室规模气固系统的有力手段。
DPS下最常用的方案为CFD-DEM,流体相基于Gidaspow提出的A类和B类模型(体积平均N-S方程的两种不同形式),采用SIMPLE算法或基于Fluent,MFIX和OpenFOAM等软件平台。颗粒相普遍采用基于软球模型的DEM(Discrete element methd)进行更新。在计算层面,CFD-DEM中流体相的求解多为隐式或半隐式算法,并行上存在巨大困难,为了降低CPU的负载,提高计算效率,目前比较流行的方法是将可并行的DEM部分使用GPU计算,而难以并行的流体部分依然采用CPU计算,即CPU-GPU异构算法。然而CPU和GPU并不共用内存,每一步下不同设备间存在复杂的异构通信,尽管较纯CPU计算已取得显著加速,但效率依然较低。
格子玻尔兹曼方法LBM(Lattice Boltzmann method)是近年来发展的一种新的计算流体力学方法,由于自身的高并行度,非常适合采用GPU计算。目前LBM在颗粒两相流中的应用主要集中在颗粒解析的DNS层次,应用LBM实现颗粒非解析的气固两相流模拟目前鲜有报道。本文提出了一种新的颗粒非解析LBM-DEM算法。其求解方程基于求解LBM-DNS中IMB的形式,但不再采用原IMB方法计算权重函数,而是将IMB方程中用于恢复无滑移条件的额外碰撞项视作力源项,通过定义格点曳力获得权重函数以修正LBM方程。同时,鉴于LBM和DEM均具备较好的并行性,本文在GPU上对该算法进行实现以发挥其最大优势。纯GPU算法避免了CPU-GPU间复杂的异构通信,较目前算法有着巨大的性能提升。
LBM-DEM方法
标准的格子Boltzmann方法(Lattice Boltzmann method, LBM)将密度分解为多个方向离散的分布函数,并在格点网格内将各分布函数碰撞迁移,通过对当前格点上各分布函数的组合还原出密度、速度等宏观量。其方程形式为:

其中 为t时刻位于x格点的第i个分布函数,
为t时刻位于x格点的第i个分布函数,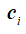 为格子速度,三维下一般采用19个方向的分布函数,即D3Q19模型,如图1所示。
为格子速度,三维下一般采用19个方向的分布函数,即D3Q19模型,如图1所示。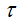 为松弛因子,由粘度确定,
为松弛因子,由粘度确定, 为平衡分布函数,由当前格点的密度和速度确定:
为平衡分布函数,由当前格点的密度和速度确定:

式中 为运动粘度,
为运动粘度,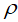 为密度,u为速度,
为密度,u为速度, 为格子声速,
为格子声速, ,c为空间步长与时间步长大小之比,当空间步长与时间步长相同时
,c为空间步长与时间步长大小之比,当空间步长与时间步长相同时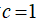 。
。 为权重系数。
为权重系数。

流体速度、压力和密度可由下式更新:

02 颗粒运动——DEM方法

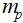 为颗粒质量,
为颗粒质量,  为颗粒速度,
为颗粒速度,  为颗粒受到的碰撞力,
为颗粒受到的碰撞力,  为颗粒受到的曳力,
为颗粒受到的曳力, 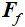 为浮力,
为浮力,  为重力加速度。
为重力加速度。
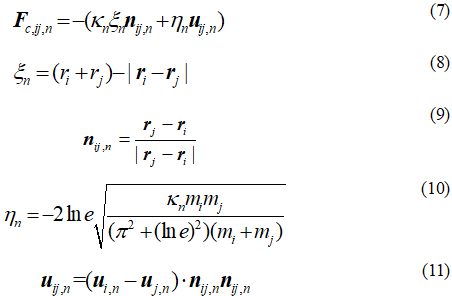
 分别为第i个颗粒的位置、半径和质量。i和j分别为相互碰撞的颗粒i和j,
分别为第i个颗粒的位置、半径和质量。i和j分别为相互碰撞的颗粒i和j,  为法向刚性系数,
为法向刚性系数, 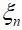 为重叠量,
为重叠量,  为单位法向矢量,
为单位法向矢量,  为法向阻尼系数,
为法向阻尼系数,  为颗粒相对速度的法向分量。
为颗粒相对速度的法向分量。03 流固耦合
流体和颗粒间的耦合通过颗粒所受曳力实现。单颗粒的受力可基于Wen-Yu曳力描述,其形式为:

其中 为颗粒雷诺数,
为颗粒雷诺数, 为滑移速度,
为滑移速度, 。r为颗粒半径,
。r为颗粒半径,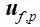 为颗粒位置处的流体速度。
为颗粒位置处的流体速度。 为颗粒位置处的固相体积分数。
为颗粒位置处的固相体积分数。
浸入运动边界法引入了格子控制体和格子固含率的概念,即计算以流体格点为中心的立方单元内固体体积所占比重,图3为以xy面为例的示意。基于非平衡态反弹和流固分相的思想,在标准单松弛的LBM中引入额外碰撞项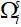 描述固体作用,则公式(1)修正为:
描述固体作用,则公式(1)修正为:
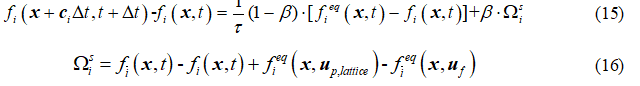
式中 为格点上的固体速度,
为格点上的固体速度,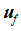 为格点上的流体速度,
为格点上的流体速度, 即格子固含率,-i代表与i反向。
即格子固含率,-i代表与i反向。 为权重函数,控制流体碰撞算子和额外碰撞项的计算比重,满足
为权重函数,控制流体碰撞算子和额外碰撞项的计算比重,满足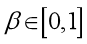 。
。 为1时完全由固体控制,公式(15)还原为标准反弹格式,
为1时完全由固体控制,公式(15)还原为标准反弹格式, 为0时完全流体控制,方程还原为标准的单松弛LB方程。求解DNS问题时,传统IMB的
为0时完全流体控制,方程还原为标准的单松弛LB方程。求解DNS问题时,传统IMB的 和网格内颗粒对流体作用力形式为:
和网格内颗粒对流体作用力形式为:


经典的浸入运动边界法在描述颗粒解析的气固两相流系统中取得了重要成功,由于DNS系统下流体网格比颗粒网格小一个数量级,加和颗粒内所有的流体格点的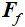 即为颗粒所受合力,则牛顿第三定律天然满足,且基于固含率实现对边界的平滑描述。在颗粒非解析的模拟系统中,颗粒尺寸比流体网格小一个量级,基于曳力公式推导的颗粒曳力和LB方程下推导的流固耦合作用力(18),其计算过程相对独立导致二者大小并不匹配,需要进行统一。本文将公式(15)中的额外碰撞项近似视为力源项,提出一个 新的流固耦合方案如下,由图3(b)所示,假设格点内存在一个等效颗粒球,其速度为
即为颗粒所受合力,则牛顿第三定律天然满足,且基于固含率实现对边界的平滑描述。在颗粒非解析的模拟系统中,颗粒尺寸比流体网格小一个量级,基于曳力公式推导的颗粒曳力和LB方程下推导的流固耦合作用力(18),其计算过程相对独立导致二者大小并不匹配,需要进行统一。本文将公式(15)中的额外碰撞项近似视为力源项,提出一个 新的流固耦合方案如下,由图3(b)所示,假设格点内存在一个等效颗粒球,其速度为 ,定义等效粒径
,定义等效粒径 由下式给出:
由下式给出:

其中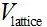 为网格体积,可为1。则基于
为网格体积,可为1。则基于 和
和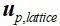 ,通过公式(14)或(15)-(18)计算出等效颗粒曳力
,通过公式(14)或(15)-(18)计算出等效颗粒曳力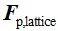 ,令LB获得的流固作用力与该等效曳力相等,即
,令LB获得的流固作用力与该等效曳力相等,即 ,则由公式(18)得出
,则由公式(18)得出 形式为:
形式为:

通过上述公式取代公式(17),即可对流场施加流固作用力,同时消除了传统IMB方法计算受力时,权重函数存在粘度项导致粘度依赖的缺陷。
GPU实现
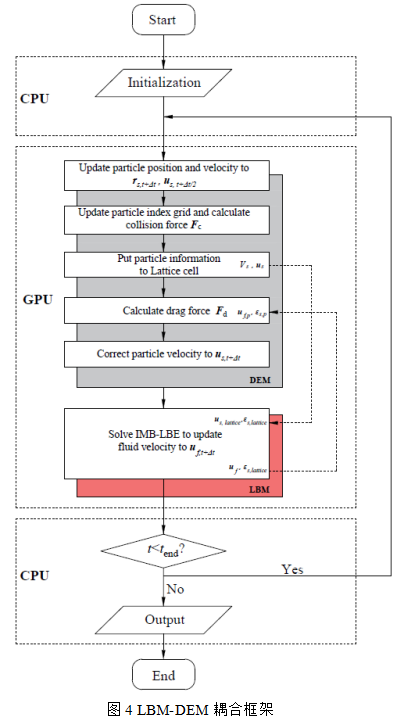
LBM-DEM准确性验证
首先,通过鼓泡流化床与CFD-DEM的结果进行对比。这里基于Lu的CFD-DEM算例,其采用CPU基的MFIX求解器完成流场的计算,基于自主实现的GPU求解器完成DEM的计算并完成二者耦合。本节基于完全GPU实现的LBM-DEM求解器求解该算例,所有物理参数与Lu的设置完全相同。速度入口采用标准平衡分布格式,壁面为标准反弹格式,出口为一阶外插,每两个格子步长更新一次颗粒邻居列表,曳力采用Wen-Yu形式。物理量对应格子单位下的无量纲参数如表1所示。

这里对比了本文的耦合方案以及WANG等人提出的不修正IMB耦合方案。不同时刻下的瞬态颗粒分布如图5所示。由图5(a), t=0.05s时顶部颗粒开始向上运动,两侧和底部颗粒由于气速较小颗粒向下沉降;t=0.1s时达到一定高度后,除顶部颗粒继续向上运动外,中部颗粒开始向下沉降,非均匀结构即将形成;t=1.0s后系统基本达到了动态平衡,体系内同时存在着向上和向下运动的颗粒聚团,颗粒分布与Lu的结果定性吻合。基于WANG等人提出的传统IMB耦合方案结果如图5(b)所示,各个时刻下颗粒始终沉降堆积在床层底部,并没有出现流化现象。图6为不同耦合方案下计算的瞬态压降曲线,与Lu的结果对比。原始的修正方案下,由于颗粒没有流化,床层压降远低于文献结果,表明传统的耦合方式在此粘度下已不再适用,而基于本文提出的耦合方案,床层压降在t=1s后保持了动态稳定,平均压降为8.48Pa,相较于CFD-DEM结果(8.37Pa)误差仅1.31%,表明本文提出的LBM-DEM算法可以得到准确的动力学结果,消除了原LBM-DEM的局限。

02 流域转变
 =53μm的FCC颗粒,颗粒总数为443000,初始床层空隙率约为0.37,其余参数详见表2。
=53μm的FCC颗粒,颗粒总数为443000,初始床层空隙率约为0.37,其余参数详见表2。
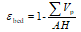 .其中A为底面积,
.其中A为底面积,  为单颗粒体积。
为单颗粒体积。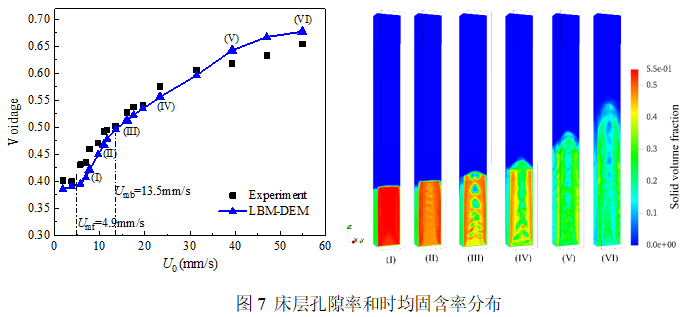
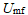 和
和 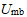 为实验测定的最小流化速度和最小鼓泡速度。当入口速度大于
为实验测定的最小流化速度和最小鼓泡速度。当入口速度大于 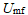 时,床层空隙率开始快速增长,随着气速进一步增大,空隙率的提升量逐渐减小。曲线平均误差为4.13%,最大误差在
时,床层空隙率开始快速增长,随着气速进一步增大,空隙率的提升量逐渐减小。曲线平均误差为4.13%,最大误差在 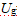 =5.69mm/s处为9.01%,均满足误差低于10%的要求。由图7,当入口速度在
=5.69mm/s处为9.01%,均满足误差低于10%的要求。由图7,当入口速度在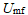 和
和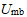 之间的范围,流动应为均匀的散式流化。由(III)当气速超过
之间的范围,流动应为均匀的散式流化。由(III)当气速超过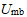 后,系统内产生了均匀上升的气泡,表明LBM-DEM模拟的流动结构与实验测定的最小流化速度和鼓泡速度范围基本吻合。随着气速进一步提高,由(IV)流动结构已经由鼓泡流化转向节涌流化;随着气速增大,颗粒运动更加剧烈。由(VI),流型已出现向湍动流化过渡的趋势。本文提出的LBM-DEM方法复现了颗粒群在微流化床中的流域转变,定性和定量结论均与实验结果一致,表明该算法可作为模拟气固两相流动的可行方案。
后,系统内产生了均匀上升的气泡,表明LBM-DEM模拟的流动结构与实验测定的最小流化速度和鼓泡速度范围基本吻合。随着气速进一步提高,由(IV)流动结构已经由鼓泡流化转向节涌流化;随着气速增大,颗粒运动更加剧烈。由(VI),流型已出现向湍动流化过渡的趋势。本文提出的LBM-DEM方法复现了颗粒群在微流化床中的流域转变,定性和定量结论均与实验结果一致,表明该算法可作为模拟气固两相流动的可行方案。基于该方法对快速流化进行模拟研究。为了更好展现颗粒运动时的非均匀结构,这里基于三维矩形薄板复现快速流化现象。针对流场,底部为速度入口,顶部一阶外插出口,x法向面为标准反弹边界,y法向面为周期边界。对于颗粒,颗粒沿y方向和z方向运动均做周期运动。模拟使用的总颗粒数为2212848,初始固含率约为0.09,采用Wen-Yu曳力形式。模拟的相关参数如表3所示。
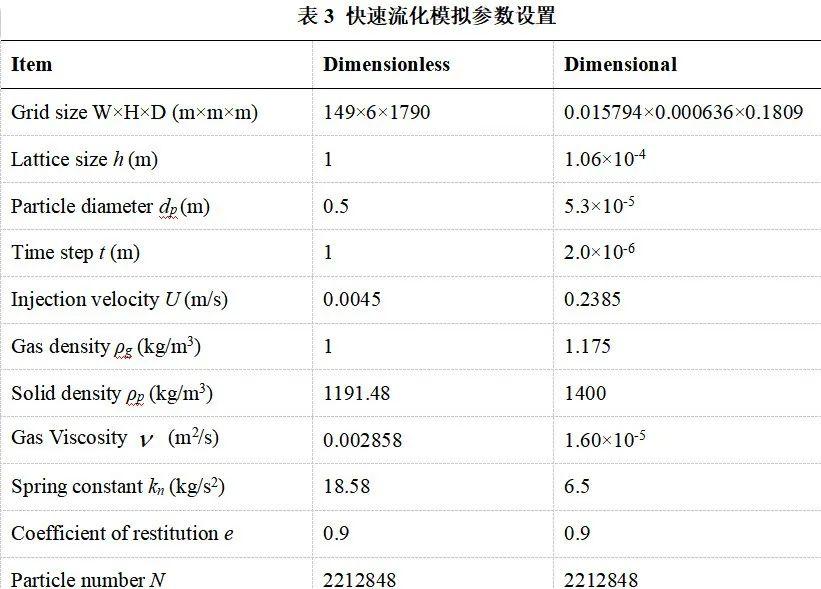

应用该算法得到了超高解析度的气体-颗粒分布,如图8所示。t=1s后流化床内颗粒结构达到完全演化,整个床层都分布着颗粒聚团,同时床层内存在明显的稀密相结构,密相下颗粒的浓度较高,对应气体速度较低,集中在底部和边壁,而稀相内颗粒浓度较低对应气体的速度较高。颗粒整体分布呈现上稀下浓,中间稀两侧浓的非均匀结构,与Li等人的模拟和实验结果定性一致。基于t=2s后的时均结果得到快速流化下轴向固含率如图9所示。颗粒浓度沿轴向分布为一条S型曲线,与Li and Kwauk在10m床高中的实验规律基本吻合,表明了该算法在分析快速流化问题中的适用性。

04 LBM-DEM速度测试

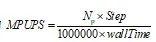 ,其中Step为更新总步数。统计物理时间1s下LBM-DEM的计算总时长以及LBM部分和DEM部分的MLUPS和MPUPS,结果如图11所示。case C中包含160万以上的流体网格和220万以上的颗粒,使用该算法仅需2.071h即可完成物理时间1s的更新,展现了极高的计算效率。case D计算1s的时间为16.25h,为case C的7.85倍,与其计算规模较case C扩大8倍基本相当,表明该算法的计算时间是随计算规模线性增长的,增大流体网格和颗粒数量并不会降低程序的计算速度。随着颗粒规模的增大,MPUPS持续增加并逐渐达到峰值速度,case D下MPUPS为157.74。基于MLUPS和MPUPS可在已知求解规模下大体预估程序的整体求解时间。本文提出的LBM-DEM具备远超传统CFD-DEM的计算效率,较纯CPU算法可带来两个数量级的加速提升,较CPU-GPU异构算法也能实现数倍加速,非常适合求解大规模气固颗粒系统。尽管计算设备存在差异不能单纯比较计算时间,但本文提出的LBM-DEM作为纯GPU实现的气固两相流算法,未来随着GPU硬件更新将具备更加显著的优势和应用前景。
,其中Step为更新总步数。统计物理时间1s下LBM-DEM的计算总时长以及LBM部分和DEM部分的MLUPS和MPUPS,结果如图11所示。case C中包含160万以上的流体网格和220万以上的颗粒,使用该算法仅需2.071h即可完成物理时间1s的更新,展现了极高的计算效率。case D计算1s的时间为16.25h,为case C的7.85倍,与其计算规模较case C扩大8倍基本相当,表明该算法的计算时间是随计算规模线性增长的,增大流体网格和颗粒数量并不会降低程序的计算速度。随着颗粒规模的增大,MPUPS持续增加并逐渐达到峰值速度,case D下MPUPS为157.74。基于MLUPS和MPUPS可在已知求解规模下大体预估程序的整体求解时间。本文提出的LBM-DEM具备远超传统CFD-DEM的计算效率,较纯CPU算法可带来两个数量级的加速提升,较CPU-GPU异构算法也能实现数倍加速,非常适合求解大规模气固颗粒系统。尽管计算设备存在差异不能单纯比较计算时间,但本文提出的LBM-DEM作为纯GPU实现的气固两相流算法,未来随着GPU硬件更新将具备更加显著的优势和应用前景。
结论