迁移学习!SCI二区开源代码推荐|结合理论边界和深度对抗网络的迁移学习开集故障诊断
迁移学习是当前故障诊断领域的研究热点,然而针对其开源代码较少,小编整理搜集了一些开源代码与大家进行分享。本期分享的是结合理论边界和深度对抗网络的迁移学习开集故障诊断,该论文发表于Neurocomputing期刊,并提供有该作者原创的开源代码,因此这篇开源代码适合参考借鉴并在上面进行改进学习,适合具备一定的深度迁移学习基础知识的学习者。该方法很贴合实际工程应用场景,非常值得阅读!
1 论文基本信息
论文题目:Combining the theoretical bound and deep adversarial network for machinery open-set diagnosis transfer
论文期刊:Neurocomputing
Doi:https://doi.org/10.1016/j.neucom.2023.126391
论文时间:2023年
作者:Yafei Deng, Jun Lv, Delin Huang, Shichang Du
机构:
State Key Lab of Mechanical System and Vibration, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; Department of Industrial Engineering and Management, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; Faculty of Economics and Management, East China Normal University, 200241 Shanghai, China; College of Intelligent Manufacturing and Control Engineering, Shanghai Polytechnic University, China
2 摘要
3 目录
4 引言
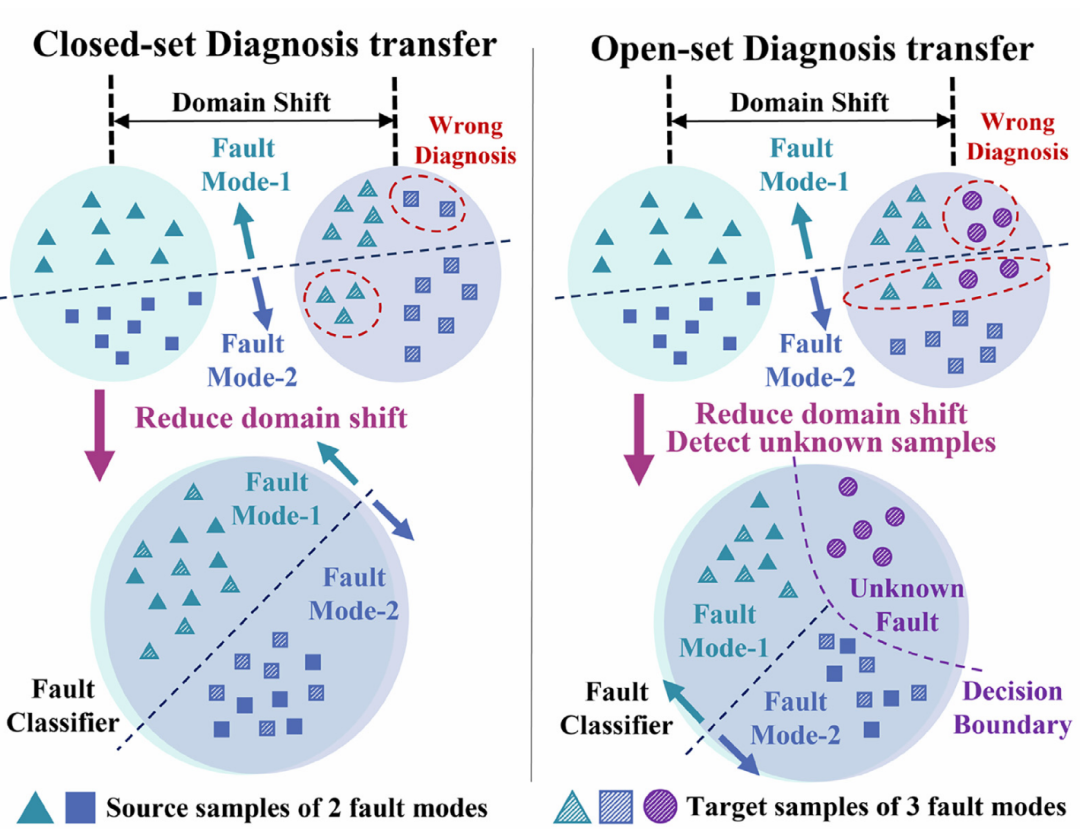 图1 CSDT和OSDT的对比图
图1 CSDT和OSDT的对比图
(1) 不确定决策边界:在不知道未知样本和已知样本之间的相关程度的情况下,很难确定一个固定的决策界来识别未知样本和已知样本。在开放程度较大的情况下,使用过紧的决策界会忽略一些未知的样本,而在开放程度较小的情况下,使用过于宽松的决策界会包含一些已知的样本。
(2) 交互性负迁移:在模型训练过程中,两个目标相互影响。详细地说,已知和未知的目标样本在领域偏移大的情况下会变得混乱,使得更难学习准确的决策边界。因此,这些误分类的样本,属于共享(私有)空间,但被认为是私有(共享),将产生不利影响的分布匹配,这进一步误导决策边界学习。
为了克服上述挑战,我们提出了一种新的理论引导的深度对抗网络来检测新出现的故障并减少领域差异。通过最小化理论推导的误差界,优化开集检测风险和域不变学习风险,在理论上保证了类间的可分性和类内的紧凑性。此外,设计了两阶段渐进式学习策略来抑制交互式负迁移。最后,采用基于对抗的机制使模型具有从不平衡数据中学习判别表示的能力,在不同的开放程度下都能表现出较好的泛化能力。
 图2 概述了OSDT问题的TPTLN方法
图2 概述了OSDT问题的TPTLN方法
图2中,(a)开集设置下的最终状态示例,其中源域和目标域包含几个已知的共同的故障类(图中标记的三角形和正方形),并且目标域还包含源域中不包括的未知故障类(图中的圆圈)。(b)分离阶段后的情况:首先构造源域已知故障的分类边界,使TPTLN能够实现诊断。其次,构造一个由粗到细的决策边界,将已知类和未知类的目标样本分开。(c)靠近阶段之后的情况。采用对抗性分布对齐策略靠近共享空间中的源域和目标域样本。(d)在分离阶段和靠近阶段之间进行渐进学习后,迭代直到收敛的情况下,未知类的目标样本将被分离出共享空间,而已知类的目标样本将靠近它们的源域对应的类。主要贡献概述如下:
(1)我们对OSDT的情况下的迁移学习进行探索,其中的目标域不仅包含与源域共享的标签空间,也包含不在源域中的私有标签(新的未知故障类型)。
(2)设计了一种渐进式学习结构TPTLN,分别实现目标样本划分(分离阶段)和领域分布对齐(靠近阶段)。该方法将不确定性校正、自适应开放度估计和加权分布模块附加到两阶段学习过程中,能够更好地适应较大的领域迁移,有效避免了同一模型内的交互负迁移问题。
(3)在理论界分析的指导下设计了TPTLN。最小化源域损失获得源域分类器,优化分布差异的目标是学习领域不变特征,通过提出的校正相似度和领域一致性得分控制开集风险,提供一个自适应的决策边界来检测目标未知样本,适应不同程度的目标数据开放性。
(4)设计了不同领域迁移程度和开放度变化情况下的开集诊断迁移任务,验证了模型的有效性。选取了7个具有代表性的模型作为基准模型,通过多种可视化方法验证了模型在提高诊断精度和增强迁移鲁棒性方面的性能。
5 相关工作
5.1 开集诊断迁移
开集迁移诊断的目的是从目标域检测新出现的未知故障类,同时正确地将已知故障类的诊断知识从源域迁移到目标域。近年来,已经提出了几种方法来解决计算机视觉领域中的开集领域自适应问题,例如OSBP [15],STA [16]和CMU [17]。也有一些研究人员正在为工业应用进行探索性工作。Li等人首先提出了一种深度对抗迁移学习网络(Deep Adversarial Transfer Learning Network, DATLN),该网络受到OSBP方法的启发,并已成功应用于旋转机器故障检测[18]。DATLN通过一个对抗性的二元分类器来确定决策边界,当对应样本的分类概率超过固定阈值(通常设置为0.5)时,未知故障将被识别。Zhang等人开发了一个实例级加权对抗网络来解决OSDT问题[19]。研究者提出了目标域样本的实例级权重来描述与源域类的相似性,该权重由目标域样本的相似性得分得到,并采用熵最小化方法来增强目标离群点检测。Zhu等人提出了一种具有多个辅助分类器的对抗网络(Adversarial Network with Multiple Auxiliary Classifier, ANAMC), 该网络开发了多个分类器来校准OSBP方法中的阈值设置[20]。这些辅助分类器可以更好地利用具有代表性权重的领域知识,这有助于更灵活地制定准确的决策范围,而不是将某个固定阈值下的所有目标数据强制为一个类别。
回顾最近的文献,现有的OSDT模型缺乏必要的理论分析,从而忽略了潜在的改进方案,导致产生了受到客观影响的解决方案[21]。本文将理论界分析方法引入OSDT模型设计中,填补了OSDT模型设计的空白,使OSDT模型能够以无监督的方式检测新出现的目标离群数据。此外,设计了渐进式对抗学习策略,以抑制互动负迁移下大程度的开放性和领域迁移。
6 所提出的方法
 图3 概述了OSDT问题的TPTLN方法
图3 概述了OSDT问题的TPTLN方法

6.2 分离阶段
6.2.1 源域风险
开集风险表示模型区分未知目标类和已知目标类的能力,应该注意的是,首先应该准确评估开放性
6.2.2.1 基于不确定度校准源域鉴别器
我们设计了多个二分类的鉴别器
6.2.2.2 基于一致性得分的目标域鉴别器
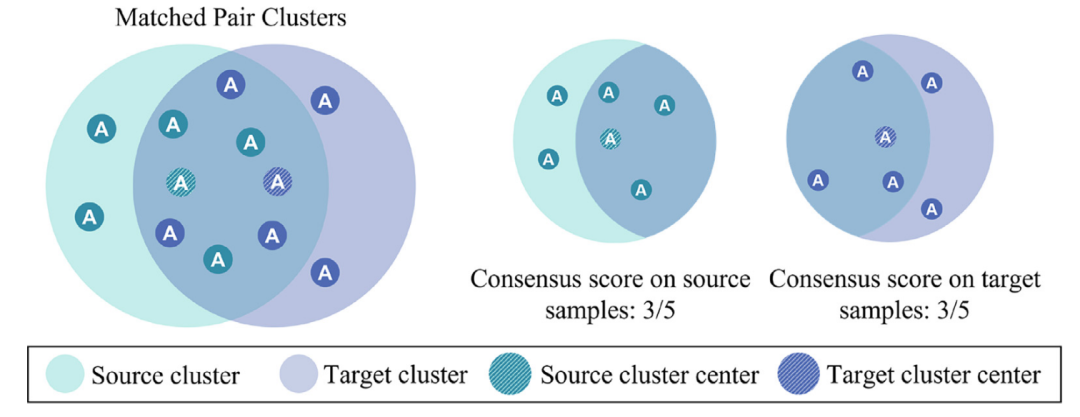 图4 领域一致性得分的图示
图4 领域一致性得分的图示
在靠近阶段,应减少源域和目标域之间的分布差异以实现学习领域不变的特征。需要注意的是只有源域和目标域所共享的空间需要对齐。 为此,我们提出了一种加权分布风险优化策略来促进源域和目标域已知类别的对齐,并抑制源域和目标域未知类的对齐。
6.3.1 加权分配风险优化
为了给每个目标域样本赋予不同的权重,目标域鉴别器
7 实验
7.1 关键对比方法和评估指标
OSBP(Open Set Domain Adaptation by Backpropagation)旨在构建一个决策边界来检测未知的目标域样本。训练分类器以在源域样本和目标域样本之间建立边界,而训练生成器以使目标样本远离边界。
STA(Separate to Adapt)采用两阶段网络结构来解决开集迁移学习问题,其中第一阶段通过探索源域数据来训练识别目标未知数据,第二阶段训练在已知类的范围内适应分布。
CMU(Calibrated Multiple Understanding)提出了一种新的可迁移性度量来检测离群数据,该度量由互补中的不确定性量的混合来估计:熵,置信度和一致性,定义在由多分类器模型校准的条件概率上。
DATLN(Deep Adversarial Transfer Learning Network)首先讨论了在工业场景中迁移诊断知识的开集设置。对抗分类器被设计为在源域和目标域中对齐样本(具有已知类别),并检测具有未知类别的样本。
IW-OSDA(Instance-Level Weighted Open-set Domain Adaptation)将离群值分类器结合到基于对抗的网络中,以增强OSDT问题的未知故障样本检测。由领域差异度得到的实例权重用来描述目标域样本与源域类的相似度。
为了全面评估TPTLN和其他基线方法,两个广泛使用的评估指标,所有类别的标准化准确度和仅已知类别的标准化准确度
7.2.1 实验结果
表9a 基于轴承任务的准确率对比
表9b 基于齿轮箱任务的准确率对比
7.2.2 性能分析

图8 每个类中目标实例的权重的平均值
(a) 轴承OSDT任务的结果; (b) 齿轮箱OSDT任务的结果。
为了直观地评估所提出的方法的性能,在所有OSDT任务中学习的目标域样本的实例级权重进行了研究。由于STA、CMU和IWOSDA模型通过分配不同的权重来区分离群样本,因此给出了这些方法的结果以供比较,可视化结果如图8所示,其中目标离群实例的权重以红色标记。
7.2.3 性能分析

图9 齿轮箱任务T1上的域不变特征的可视化
为了比较模型性能并反映所提出方法的优点,使用t分布随机邻居嵌入(t-SNE)算法[28]来可视化从生成器
8 总结
编辑:曹希铭
校核:李正平、张泽明、张勇、王畅、陈凯歌、赵栓栓、董浩杰
该文资料搜集自网络,仅用作学术分享,不做商业用途,若侵权,后台联系小编进行删除







