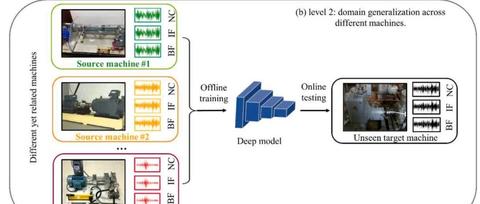
深度学习专题之数据预处理 | 一维数据二维图像化方法分享(CWT、GAF、MTF)
本文摘要:(由ai生成)
本文探讨了一维数据二维图片化在深度学习故障诊断领域的应用。通过CWT、GAF和MTF等方法将一维数据转换为二维图像,有助于特征提取、模型训练和异常检测。这些方法可捕捉信号的时频特征、时间依赖性和状态转移概率,提升时间序列分析效果。该应用为时间序列分析领域提供了新的视角,有助于处理和分析大量时间序列数据。文章还提供了Python实现代码,为实际应用提供了便利。
通过二维图片化的方法,可以提取出一维数据中隐藏的重要特征和模式,有助于后续的特征分析和模式识别。同时,二维图片化的数据更适合于深度学习模型的训练和应用,能够更好地捕捉数据的空间信息和相关性,提高模型的准确性和稳定性。因此,一维数据二维图片化在深度学习故障诊断领域具有重要的应用价值。适合于深度学习、故障诊断、信号处理领域学习者。
目录
1 前言
2 连续小波变换
2.1 连续小波变换的基本原理
2.2 利用连续小波变换二维图像化步骤
2.3 python实现
3 格拉姆角场
3.1 格拉姆角场的基本原理
3.2 利用格拉姆角场二维图像化步骤
3.3 python实现
4 马尔可夫转移场
4.1 马尔可夫转移场的基本原理
4.2 利用马尔可夫转移场二维图像化步骤
4.3 python实现
5 结论
1 前言
二维图片化是将一维数据转换为二维图像的过程,通过这种转换,可以将原始的一维数据以更直观的方式展示出来,便于人们观察和分析数据的特征和趋势。这种技术在信号处理、数据分析、图像处理等领域中被广泛应用。将一维数据转换为二维图片的目的和意义主要有以下几点:
可视化展示:二维图片比一维数据更直观易懂,可以直观地展示数据的变化趋势、周期性、异常模式等,帮助人们更好地理解数据。
特征提取:通过二维图片化的过程,可以提取出数据中的重要特征信息,例如频率、幅度、周期性、相位等,这些特征对于后续的数据分析和模式识别非常有用。
模型训练:二维图片化的数据更适合于深度学习模型的训练和应用,能够更好地捕捉数据的空间信息和相关性,提高模型的准确性和稳定性。
异常检测:通过对二维图片化的数据进行分析和比较,可以更容易地发现数据中的异常模式或异常行为,有助于故障诊断和预测。
可解释性:二维图片化的数据更易于解释和理解,有助于向非专业人员或决策者展示数据分析结果,提高决策的依据性和可信度。
数据可视化:二维图片化的数据可以用于数据可视化,帮助用户直观地探索和分析数据,发现潜在的关联和规律
一维数据二维图片化不仅提高了数据的可视化效果和直观性,还能够帮助提取重要特征、训练深度学习模型、检测异常和提高数据分析的可解释性,对深度学习故障诊断领域具有重要的应用价值。
本篇推文将介绍与深度学习故障诊断领域中一维数据二维图片化相关的信号处理方法。具体地,着墨写了以下内容:
连续小波变换(Continuous Wavelet Transform,CWT):介绍小波变换的基本原理和应用,以及如何利用连续小波变换将一维时间序列数据转换为二维图像,用于捕获信号的频率和时间信息。
格拉姆角场(Gramian Angular Field,GAF):格拉姆角场的概念和特点,以及如何使用格拉姆角场将一维时间序列数据映射为二维图像,反映数据间的相似度和差异性。
马尔可夫转移场(Markov Transition Field,MTF):将时序信号转换为二维矩阵,然后将矩阵转换为图片,用于分析序列数据的转换过程和模式。
2 连续小波变换
2.1 连续小波变换的基本原理
连续小波变换(Continuous Wavelet Transform,CWT)是一种信号处理技术,用于对信号进行多尺度分析,捕捉信号在不同频率和时间尺度上的特征。其基本原理如下:
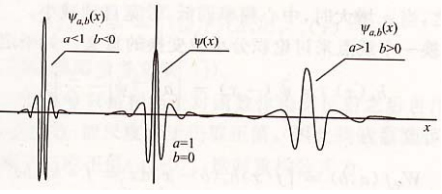
连续小波变换利用小波函数对信号进行分解和重构。小波函数是一种局部化的函数,可以在时间和频率上具有局部性质,因此可以较好地捕获信号的局部特征。连续小波变换将信号与不同尺度和频率的小波函数进行卷积,得到不同尺度下的小波系数,从而实现对信号在频率和时间上的多尺度分析。CWT的公式为:
import numpy as npimport pywtimport matplotlib.pyplot as plt# 生成随机一维数据np.random.seed(0)data = np.random.rand(1024)# 设置连续小波变换参数wavelet = 'morl' # 小波函数选择Morlet小波scales = np.arange(1, 128) # 尺度参数范围# 进行连续小波变换coefficients, frequencies = pywt.cwt(data, scales, wavelet)# 生成二维图像plt.figure(figsize=(10, 6))plt.imshow(np.abs(coefficients), extent=[-1, 1, 1, 128], cmap='jet', aspect='auto')plt.colorbar(label='Magnitude')plt.title('Continuous Wavelet Transform')plt.xlabel('Time')plt.ylabel('Scale')plt.show()

代码运行结果如图2所示。在这个示例中,我们首先生成了一个随机的一维数据 data,然后选择了 Morlet 小波作为小波函数,设置了尺度参数范围为 1 到 128,并利用 pywt.cwt 函数进行连续小波变换,最后利用 imshow 函数生成了二维图像。你可以根据实际需求调整小波函数、尺度参数范围以及数据的生成方式,以适应不同的应用场景。
3 格拉姆角场

import numpy as npimport matplotlib.pyplot as plt# 准备一维时间序列数据(示例数据)np.random.seed(0)time_series = np.random.rand(100)# 计算格拉姆矩阵gram_matrix = np.outer(time_series, time_series)# 计算角度表示(在这里进行范围限制避免无效值警告)diag_sqrt = np.sqrt(np.outer(np.diag(gram_matrix), np.diag(gram_matrix)))angle_matrix = np.arccos(np.clip(gram_matrix / diag_sqrt, -1, 1))# 生成二维图像plt.imshow(angle_matrix, cmap='jet', aspect='auto')plt.colorbar(label='Angle (radians)')plt.title('Gramian Angular Field')plt.xlabel('Time')plt.ylabel('Time')plt.show()

4 马尔科夫转移场

图5 MTF图像生成过程
import numpy as npimport matplotlib.pyplot as plt# 准备一维时间序列数据(示例数据)np.random.seed(0)time_series = np.random.randint(0, 10, 100) # 随机生成一维时间序列数据(假设取值范围为0到9)# 划分状态(假设状态范围为0到9)num_states = 10states = np.linspace(0, 9, num_states, endpoint=True)# 计算状态转移概率transition_matrix = np.zeros((num_states, num_states))for i in range(len(time_series) - 1):current_state = np.argmin(np.abs(states - time_series[i])) # 当前状态next_state = np.argmin(np.abs(states - time_series[i + 1])) # 下一个状态transition_matrix[current_state, next_state] += 1# 归一化转移概率transition_matrix /= np.sum(transition_matrix, axis=1, keepdims=True)# 生成二维图像plt.imshow(transition_matrix, cmap='jet', aspect='auto')plt.colorbar(label='Transition Probability')plt.title('Markov Transition Field')plt.xlabel('Next State')plt.ylabel('Current State')plt.xticks(np.arange(num_states), [f'{s:.1f}' for s in states])plt.yticks(np.arange(num_states), [f'{s:.1f}' for s in states])plt.show()

代码运行结果如图6所示,在这个示例中,我们生了一个随机的一维时间序列数据 time_series,然后将数据划分为10个离散的状态,并计算了状态之间的转移概率,最后使用matplotlib库生成了二维图像展示状态之间的转移关系。这种方法可以帮助理解时间序列数据中状态的变化规律和转移概率,对于某些故障诊断场景有一定的应用价值。
5 结论
2. 转换过程同时也是一种有针对性的数据处理过程,使数据的主要特征更加凸显;
3. 可以充分利用计算机视觉领域的特征提取机制,高效地提取关键特征;
随着数据采集技术的不断进步和设备的广泛应用,各种场景下产生的庞大时间序列数据亟需高效的分析方法。将时间序列转换为二维图像,并依托图像领域的研究成果进行分析,是一种崭新的突破性方法。此外,还存在一些有待挖掘的研究点,如转换过程中的数据不丢失问题。当前,时间序列分析领域相对于图像领域在研究进展上仍未有较大突破,因此这种方法可为相关领域的研究者带来全新的视角。