应力三轴度相关概念
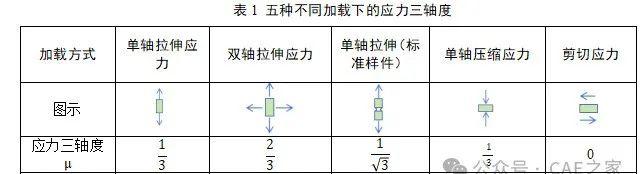
相关研究发现,应力三轴度、应变率及罗德参数是影响金属等韧性材料断裂的三个主要因素之一。在三维空间内的微元体上有三个应力分量不随坐标系改变,即为三个主应力,该三个主应力正是反映材料真实应力状态的参数,为此将材料失效时的应力状态采用应力三轴度来表示,同时Mises等效应力、静水压力等都与三个主应力相关。应力三轴度定义为平均应力与Mises等效应力之间的比例,即为:

其中:
上式中分别表示Mises等效应力,P静水压力;应力三轴度的物理意义为材料内任一点的应力张量可以分解为应力球张量和应力偏张量;应力球张量即为静水压力,会引起体积变形(即为三个主应力的状态),而应力偏张量即为等效应力反映的是形状改变(即为第四强度理论,即称为畸变能理论);即应力三轴度作为结构受力时的应力状态参数,反映了结构的体积和形状改变,通过其比值来表征材料的受力状态。
应力状态对于失效时的等效应变起着关键作用,材料所受的应力状态不同,材料内部产生的塑性变形与应力集中程度不同,材料失效应变数值也将发生变化。一般应力三轴度较大的位置,即可能等效应力较小,亦即为塑性变形较小的区域,是材料中体积变形较大,能够释放较多弹性应变的位置,且常常会出现较为严重的应力集中;而应力三轴度较小的区域,即可能等效应力较大,相对容易发生断裂。
应力三轴度会影响结构材料在受力时阻碍塑性变形和影响材料内部微晶体孔洞的增长过程,即对材料失效有非常重要作用。不同的加载工况会引起材料内部应力状态不同,其对应的应力三轴度也有所不同。
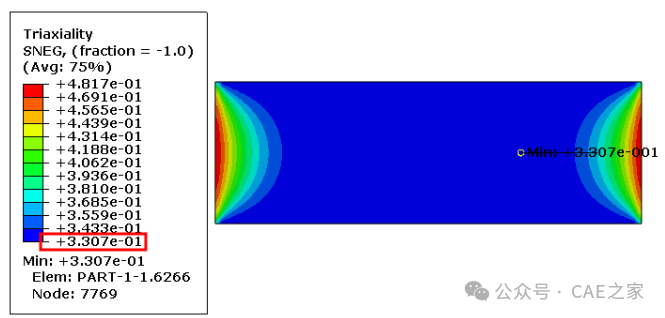
ABAQUS显式输出设置,如模拟单轴拉伸,左侧约束123自由度,右侧约束23自由度,释放1自由度,并加载1mm/s的速度(该单位采用弹性模量E为70GPa,泊松比为0.3,密度为2.7e-6kg/mm^3),分析结果中应力三轴度为0.3304与理论0.33一致。


隐式输出设置,模型同显式分析模型,但隐式的应力三轴度Mises等效应力和静水压力Press输出再进行计算得到,分析结果应力三轴度为0.3307与理论0.33一致。