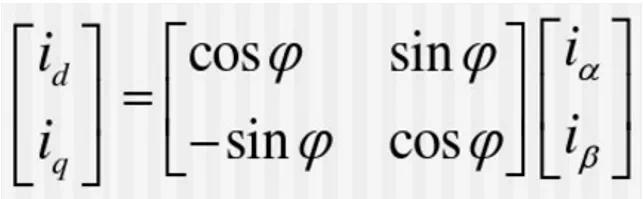PMSM的矢量控制SVPWM与坐标变换
文章摘要
矢量控制,又名磁场导向控制,是一种通过变频器控制三相交流电机的方法,通过调整输出频率、电压大小及角度来控制电机输出。它将定子电流分解为励磁和转矩电流分量,实现磁链与转矩的解耦,从而独立控制速度和磁场。坐标变换,包括Clarke和Park变换,简化了系统模型,便于控制。电压空间矢量通过SVPWM三相逆变器实现,能够精确控制电机性能。这些技术使得矢量控制成为实现高性能电机调速的重要方法。
正文
01 什么是矢量控制
矢量控制(vector control)也称为磁场导向控制(field-oriented control,简称FOC),是一种利用变频器(VFD)控制三相交流电机的技术,利用调整变频器的输出频率、输出电压的大小及角度,来控制交流电机的输出。
具体是将电动机的定子电流矢量分解为产生磁场的电流分量 (励磁电流) 和产生转矩的电流分量 (转矩电流) 分别加以控制,并同时控制两分量间的幅值和相位,即控制定子电流矢量,所以称这种控制方式称为矢量控制方式。
矢量控制就是将磁链与转矩解耦,有利于分别设计两者的调节器,以实现对交流电机的高性能调速。
其实质是将交流电动机等效为直流电动机,分别对速度,磁场两个分量进行独立控制。通过控制转子磁链,然后分解定子电流而获得转矩和磁场两个分量,经坐标变换,实现正交或解耦控制。
具体而言,有基于转差频率控制的矢量控制方式、无速度传感器矢量控制方式和有速度传感器的矢量控制方式
坐标变换:通过数学上的坐标变换方法,可以使数学模型的维数降低,参变量之间的耦合因子减少,使系统数学模型简化。
(1)Clarke变换(3s-2s)
依据磁动势F守恒的分解,将三相静止坐标系ABC下的定子电流分解为两相静止坐标系αβ分量
考虑到在坐标变换前后的总功不变,可得N3/N2=√2/√3,即
同样的,三相定子电压UABC到Uαβ的变换公式也是相同的。
变换的思想:在三相坐标通入互差120°三相交流电流的形成的旋转磁动势与两相坐标下通入互差90°两相交流电流形成的旋转磁动势是等效的。
但是可以发现,转子磁通在αβ坐标系下仍然是一个时变分量,不好做处理,需要进行下一步变换
(2)Park变换(2s-2r)
若直流电机电枢绕组以整体同步速度旋转,使其相互正交或垂直的绕组分别通以直流电流,产生的合成磁动势F相对于绕组是固定不变的,但从外部看,它的合成磁动势也是旋转的,这就是Park变换的思想。
等效原理:静止坐标系αβ下通入互差90°的交流电流iα,iβ,这样会形成一个以交流电流频率ω旋转的磁场;而在图中的dq旋转坐标系下,id,iq是一组直流电流,而dq坐标系以频率ω旋转,这样形成的旋转磁场与转换之前的旋转磁场是等效的。
因此分量分解结果是
经过Clarke-Park变换,PMSM的矢量控制框图中的蓝色虚线框中的功能已实现
其中转子位置θrel(或角度)的精确测量是控制中的精髓,对这方面的研究也层出不穷,目前使用最多的方法是霍尔传感器与增量光电编码器,也有无传感器的位置检测算法。
PMSM控制元件最多的是SVPWM三相逆变器,其包含3个开关管SA,SB,SC及其相应的3个对管/SA,/SB,/SC,共有2^3=8中状态,
若规定三相负载的某一相与电源+极接通的开关状态设为“1”态,反之,与电源-极接通的开关状态设为“0”态,则可能的8种组合为
其中有电压1~6状态,零电压状态0和7
逆变器的输出电压u(t)用空间电压矢量表示
把逆变器的8个输出状态放入空间平面中,其中Us(000)与Us(111)重合置于原点,这样形成7个电压空间矢量,每两个工作电压空间矢量相隔60°,其中6非零矢量构成正六边形的6个顶点
任意想要的逆变器输出状态都可以在空间矢量的组合中找到,这样利用空间矢量调制算法(SVPWM)用以调制αβ轴下的电压,实现PMSM的定子电流与磁链控制。