ZY哥就瞬态分析一个小术语表示道歉,但我觉得没必要,也许维持原判更好!
问题来源
作为仿真培训界新势力,我们保持留意前辈的动向。最近ZY哥出了一件小事情,我来吃个瓜。


简单来说,ZY哥收到罗经理的指出,将基于频域的瞬态分析改为基于模态叠加法的瞬态分析。感叹日华哥谦虚谨慎的态度。我们作为新势力也说几句。
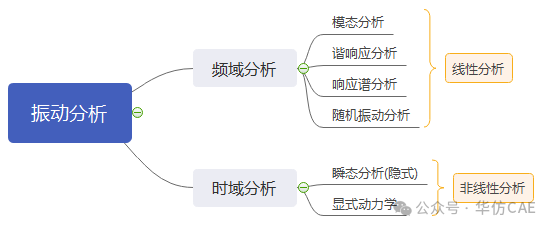
时域分析与频域分析
什么是时域分析,什么是频域分析。区分起来不要太简单。直接引用大牛的话,更有说服力!

举个具体点的例子,对于单自由度振动系统,承受任意激励:



模态叠加法
模态叠加法只能用于线性振动系统的分析。直接引用大牛的话,更有说服力!

举个具体点的例子,对于多自由度无阻尼振动系统,承受任意激励:




最后进行模态组合

到此,ZY哥的问题已经很清楚了:在模态叠加法中可以选择时域分析或频域分析,所以模态叠加法不等于频域分析。
还有,对于多自由度有阻尼振动系统,承受任意激励:


模态叠加法的优点:

模态叠加法的要点:

模态叠加法的缺点:

时域积分法
不管什么Duhamel积分,还是什么Fourier变换,其实都只能解决线性振动问题。要解决非线性问题,只能使用时域逐步积分法。这是大牛说的。



总结
总结以上内容,结论如下:
1)时域分析包含两种:逐步积分法,Duhamel积分法;
2)频域分析包含一种:Fourier变换法;
3)模态叠加法只适用于线性振动分析;
3)在模态叠加法内可以选择时域分析或频域分析;
ZY哥不必纠结
为什么我们认为ZY哥其实不用纠结这个事情呢?原因主要如下:
1)大家经常把模态分析归为频域分析,但模态分析其实是求解特征值和特征向量,和频域算法没啥关系,所以这种分类只是为了方便,另有原因,其实没必要较真。
2)ZY哥作为培训老大哥,之所以一直把模态叠加法瞬态分析称为频域瞬态分析,其实是为了强调该分析类型的线性特点。从这个意义上来说,ZY哥把握住了最重要的东西,至于算法背后到底是时域还是频域,其实不太重要。
3)谐响应分析分为完全法和模态叠加法,但不管用什么法,都改变不了谐响应分析的可靠性取决于模态分析,这是振动原理决定的。所谓时域也好,频域也罢,模态叠不叠,都不会影响ZY哥对振动的理解和对工程的经验。
4)模态叠加法瞬态分析可能用的是模态叠加原理+时域积分算法,所以从算法层面可能属于时域。但由于是线性分析,作为动力学出身的我,告诉大家,线性振动最好的分析方法是频域,所以从物理本质出发,我更支持ZY哥说的基于频域的瞬态分析,抓住了物理特点。就像把模态分析归为频域分析一样。





